PA.1 Теоретические основания
Анализ статистической мощности (Power Analysis) касается оценки ошибки второго рода при выводе на основе тестирования нулевой гипотезы. Напомним, что при отвержении или неотвержении нулевой гипотезы исследователь может сделать ошибки двух типов:
- Ошибка первого рода, связанная с неверным отвержением нулевой гипотезы в то время, как она верна. Эта ошибка традиционно считается более важной и «серьёзной» и для её контроля используется значимость получаемых значений статистики. Вероятность этой ошибки стандартно обозначается греческой буковой α (альфа).
- Ошибка второго рода, напротив, связана с принятием ложной нулевой гипотезы. Фактически, это означает, что исследователь не замечает некоего эффекта, который на самом деле есть. Вероятность этой ошибки обозначается греческой буквой β (бета).
Графически соотношение этих двух типов ошибок изображены на рис. PA.1(1).
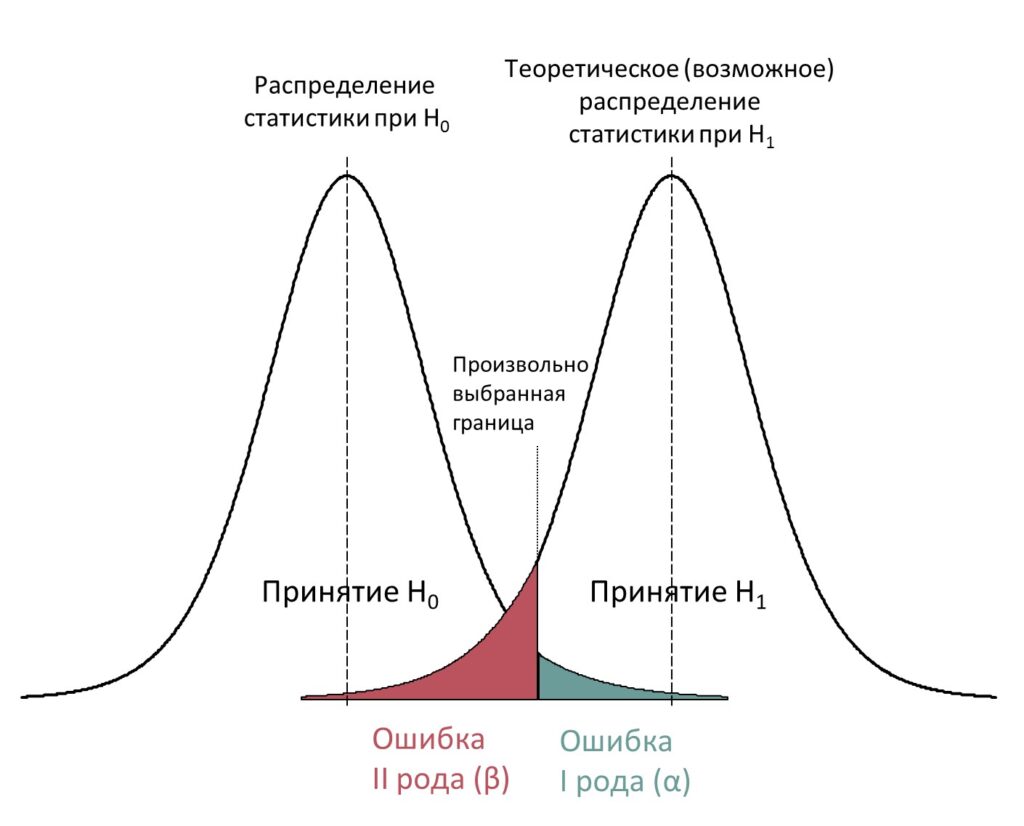 Рис. PA1(1). Соотношение двух типов статистических ошибок.
Рис. PA1(1). Соотношение двух типов статистических ошибок.
Мощностью критерия является значение 1-β (на графике это площадь распределения статистики при H1 правее выбранной границы). Таким образом, смысл коэффициента мощности – это вероятность отвергнуть H0 когда она неверна, то есть обнаружить эффект как статистически значимый в случае, когда он действительно присутствует. Чем меньше вероятность ошибки второго рода, тем больше значение мощности (1-β). В идеале значение мощности может равняться 100%, но в реальном исследовании мощность всегда ниже 100%, хотя её можно пытаться увеличить, таким образом, реже допуская ошибку второго рода. Можно выделить несколько факторов, которые могут позволить увеличить мощность критерия.
Прежде всего, это размер выборки[1]. Увеличение выборки позволяет «уловить», оценить, как значимый реально существующий небольшой эффект. Для лучшего понимания механизма этого важно заметить, что в случае отсутствия эффекта (при верной нулевой гипотезе) размер выборки мало что изменит, увеличение мощности с увеличением размера выборки относится к ситуации наличия (пусть даже и слабого) статистического эффекта. Для прояснения того, как размер выборки влияет на мощность, рассмотри элементарный пример, в котором можно использовать одновыборочный t-критерий. Допустим, мы хотим оценить изменение самооценки у студентов до и после экзамена, используя методику Дембо-Рубинштейн. Для проверки этого предположения мы можем на выборке размера n измерить самооценку перед экзаменом и после него и рассчитали разность (таким образом, сведя ситуацию с двумя зависимыми выборками к одновыборочной). Чтобы проверить нашу гипотезу об изменении самооценки можно сравнить среднюю разность с нулём – при отсутствии изменений мы, в идеальном случае, ожидаем получить в среднем ноль, а достаточно заметное отклонение разности от нуля будет говорить о наличии изменений.
Рассмотрим две идеальных ситуации: а) изменения самооценки на самом деле не происходит (то есть средняя разность равна нулю и верна статистическая гипотеза H0) и б) изменение самооценки на самом деле есть (то есть верна гипотеза H1), и оно отражается в изменении на 1 балл по используемой шкале. Стандартное отклонение разности (неизбежно присутствующее в реальных данных и связанное с индивидуальными отличиями и случайными причинами) будем считать равной 4.
Если обратиться к формуле одновыборочного t-критерия (\( t = \frac{\overline{x}-\mu}{s_x}\sqrt{n} \)), то становится видно, что размер выборки становится существенным в ситуации H1, то есть при \( \overline{x}\neq0 \): в случае H0 при заданных условиях будет равен \( t = \frac{0}{4}\sqrt{n} \), при любом n, а во случае H1 — \( t = \frac{1}{4}\sqrt{n} \), то есть растет при увеличении n[2].
Этот же эффект может быть продемонстрировано с помощью модельного эксперимента (скрипт, написанный на языке R доступен по ссылке). Он устроен так: мы смоделируем по 10000 выборок разного размера (n = 25, n = 100 и n = 400), которые могут быть получены при истинной средней разности равной 0 при стандартном отклонении 4 и в каждом случае рассчитаем и сохраним полученные статистики t, а затем построим их распределения. Они изображены на рис. PA.1(2)А. Видно, что распределения не отличаются с точностью до различий в степенях свободы (рассчитываемых как df=n-1, при небольшой выборке распределение Стьюдента с небольшим числом df имеет более «тяжелые» хвосты).
Если провести аналогичное моделирование при среднем значении сдвига равным 1 с тем же стандартным отклонение 4, обнаружится, что при увеличении выборки сдвиг t-статистики будет меняться, результат такого эксперимента представлено на рис. PA.1(2)Б. На нём отчётливо видно, что, во-первых, распределение статистики, практически не меняя свою форму, сдвигается вправо по мере увеличения выборки, и, во-вторых, при небольшой выборке \( n=25 \) t-статистика достаточно часто оказывается ниже верхнего квантиля, то есть даёт оснований отвергнуть H0, которая по нашим условиям неверна. Это как раз случаи ошибки второго рода, число которых уменьшается при увеличении выборки.
Теоретическое распределение t-статистики в этих двух примерах с учетом размера выборки представлены на рис. РА.1(2)В
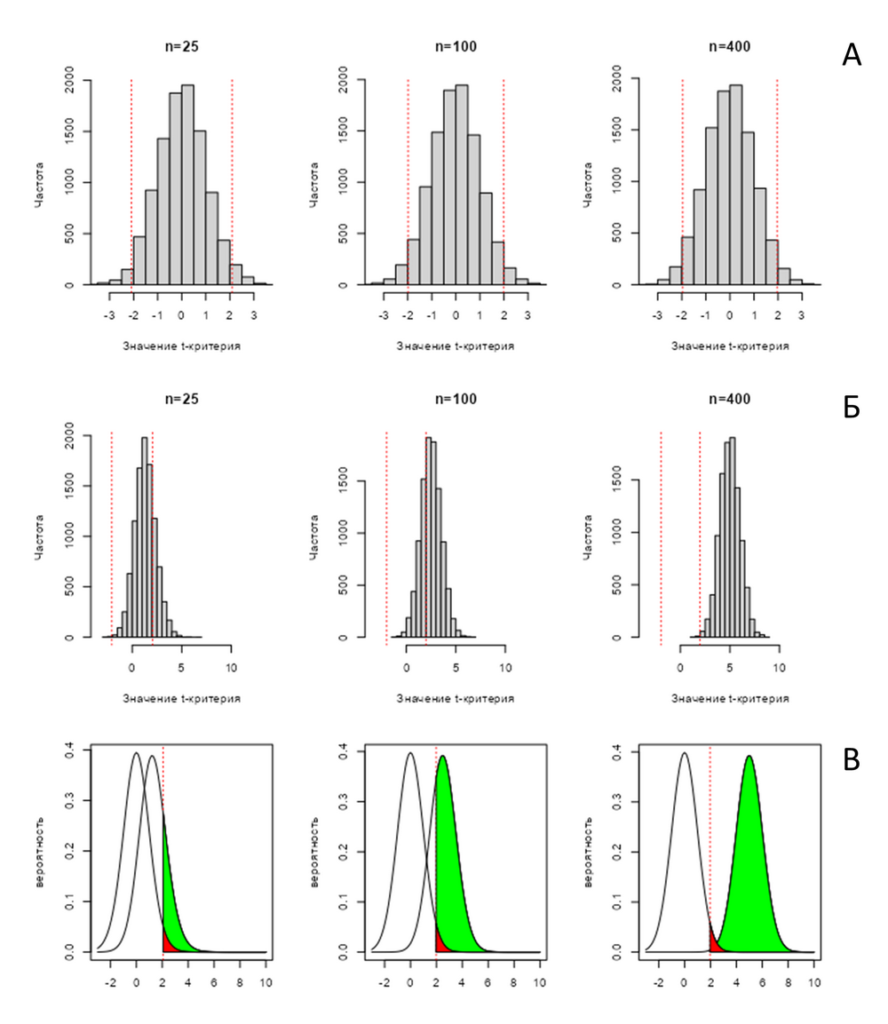 Рис. PA.1(2) Распределения эмпирических значений t-критерия, полученных на выборках разного размера (n) в случае верной нулевой (А) и альтернативной (Б) гипотезе и теоретические распределения t-статистики в этих двух случаях (В). На рисунке В красным закрашена значимость (вероятность ошибки первого рода, всегда одна и та же 0.05), а зеленым – мощность (1-вероятность ошибки второго рода).
Рис. PA.1(2) Распределения эмпирических значений t-критерия, полученных на выборках разного размера (n) в случае верной нулевой (А) и альтернативной (Б) гипотезе и теоретические распределения t-статистики в этих двух случаях (В). На рисунке В красным закрашена значимость (вероятность ошибки первого рода, всегда одна и та же 0.05), а зеленым – мощность (1-вероятность ошибки второго рода).
Также в качестве факторов, влияющих на мощность, надо указать на соотношение между ошибками первого и второго рода. В целом, при прочих равных, снижение допустимой вероятности ошибки первого рода увеличивает вероятность ошибки второго рода и наоборот. Для наглядности графически это соотношение можно найти на рисунке PA.1(1). Из него видно, что выбранная граница, обозначающая критерий принятия или отвержения нулевой гипотезы при смещении приводит одновременно к уменьшению вероятности α и увеличению вероятности β, либо, наоборот, увеличению α и уменьшению β.
В связи с этим рисунком укажем на важный момент: «возможное» распределение статистики, свидетельствующее против принятия нулевой гипотезы никогда не известно исследователю и любое единичное исследование в принципе не может быть основанием для определения этого распределения. В то же время, процедуры анализа мощности выборки могут требовать предположений об ожидаемой силе эффекта, который подразумевает то или иное смещение статистики. Такие предположения могут быть основаны на предшествующих исследованиях или каких-то других соображениях, но важно понимать их условность. При анализе мощности исследователь сталкивается с необходимостью некоторых предположений о тех или иных параметрах, характеризующих исследуемый эффект. Наиболее часто приходится устанавливать уровень значимости (максимальную вероятность совершения ошибки первого рода) и размер статистического эффекта. В качестве примера можно привести одну из задач, которая решается с помощью анализа мощности – определение минимального размера выборки, на которой с определенной вероятностью ошибок первого и второго рода эффект определенной силы будет оценен как значимый. Для проведения вычислений должны быть определены три параметра – α (оценка вероятности ошибки I рода), 1-β (статистическая мощность) и коэффициент величины статистического эффекта. Вероятности ошибок обычно устанавливаются в соответствии с общепринятыми границами – 0.05 для α и 0.80, 0.90 или 0.95 для 1-β. Это достаточно произвольные значения, которые закладывают в качестве исходных значений при определении предполагаемого размера выборки.
Если говорить в общем, основными параметрами, использующимися в анализе мощности, являются:
- Размер выборки
- Размер статистического эффекта
- Критический уровень значимости α (вероятность ошибки первого рода)
- Мощность (1-β) – вероятность не совершить ошибку второго рода.
Анализ построен на том, что, зная три из этих параметров, можно вычислить четвертый. Читатель может заметить, что при расчете размера выборки на этапе планирования эксперимента исследователь должен принять ряд априорных допущений – он должен установить прогнозируемый размер эффекта, а также выбрать уровни вероятностей α и β. Эти решения чаще всего основываются на традиции и анализе существующей литературы, практических соображениях и т.п., но в конечном итоге зависят от решения исследователя. Это стоит иметь в виду как ограничение такого рода анализа, но, тем не менее, он может быть полезен как с точки зрения планирования исследования, так и анализа уже полученных результатов.
Основные принципы анализа мощности.
Техника расчета в анализе мощности достаточно сложна, мы ограничимся кратким описанием общих идей, используя для иллюстраций достаточно прозрачный вариант анализа мощности для t-критерия Стьюдента.
Важная идея – это использование силы эффекта (d Коэна для t-критерия) как меры «сдвига» распределений статистики в условиях нулевой и альтернативной гипотезы. Напомним, что d Коэна в самом простом случае двух зависимых выборок вычисляется как разность средних выборок деленая на стандартное отклонение этой разности (подробнее см. Приложение 4):
\[ d=\frac{\overline{x}-\overline{y}}{s_{pooled}} \]
В случае совпадения оценок средних в двух выборках d=0 и распределения оцениваемого параметра совпадают. При увеличении размера статистического эффекта (увеличения модуля d) распределения начинают «расходиться». В допущении, что измеряемый параметр имеет нормальное распределение и однородную дисперсию (то есть, дисперсии в группах не различаются), коэффициент d может быть пересчитан в степень «расхождения» распределений средних в популяциях, соответствующих двум сравниваемым выборкам.
На рисунке PA.1(3) схематически изображены два распределения разности средних – одно соответствующее H0, а второе – соответствующее H1 при заданной величине эффекта (d) и размере выборки (n), определяющих сдвиг распределения (так называемый параметр нецентральности распределения Стьюдента (noncentrality parameter))[3].
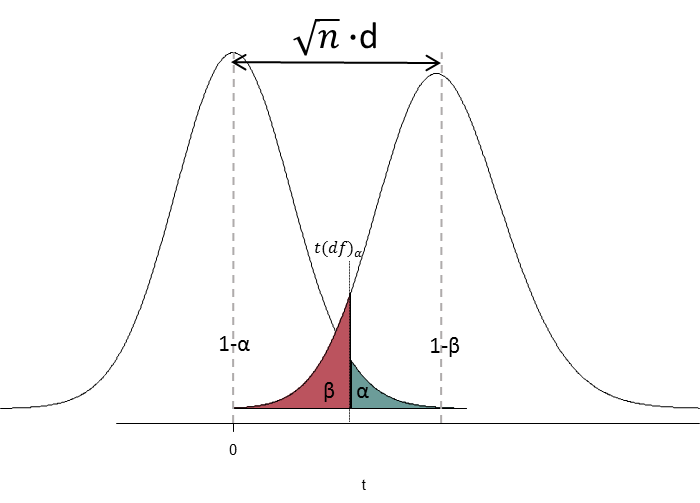 Рис. PA.1(3). Распределения, соответствующие H0 и H1 при заданной величине эффекта (d) и размере выборки (n), определяющих сдвиг распределения.
Рис. PA.1(3). Распределения, соответствующие H0 и H1 при заданной величине эффекта (d) и размере выборки (n), определяющих сдвиг распределения.
Если мы рассчитываем статистическую мощность (1-β), то она может быть рассчитана как функция от
- Размера эффекта (чем меньше распределения «перекрываются», тем больше мощность при прочих равных);
- Размера выборки (чем больше размер выборки, тем меньше дисперсия средних и тем больше мощность);
- Уровня α (чем меньше α, тем меньше мощность).
Таким образом, проведя исследование, мы можем использовать имеющиеся у нас значения размера эффекта, используемого нами уровня значимости (например, стандартные 0.05) и размеры выборки, мы можем вычислить эмпирическую мощность нашего анализа. Алгоритмически эта задача решается путем нахождения площади под кривой нецентрального (noncentral) распределения Стьюдента с соответствующим размеру выборок числом степеней свободы и коэффициентом смещения (non-centrality parameter) равным \( \sqrt{n}*d \) , отсекаемого квантилем стандартного распределения Стьюдента, соответствующего установленному значению α. Например, в случае двух зависимых выборок при проверке двухсторонней гипотезы, \( d=0.5, α=0.05 \) и размере выборок 50 значение мощности составляет 0.934. По содержанию, это оценка вероятности отвергнуть нулевую гипотезу при условии, что она не верна (то есть не допустить ошибку второго рода).
Аналогично, можно провести и другие расчеты, например, имея предположения об ожидаемой силе эффекта, установив уровень значимости α и желаемую мощность (1-β), можно рассчитать рекомендуемый размер выборки, на которой с заданной достоверностью будет обнаружен эффект ожидаемого размера. Например, если при сравнении средних в двух независимых выборках исследователь ожидает получить достаточно сильный эффект (d=0.8), при этом задан уровень значимости 0.05 и мощность равная 0.8, то рекомендуемый минимальный размер выборки оказывается равен 26 (в каждой из групп).
В случае анализа мощности других критериев и статистик может потребоваться указание дополнительных параметров (например, в дисперсионном анализе – число групп), а также по-разному рассчитываемая величина статистического эффекта, но базовая идея остается такой же – при указании эмпирических или предполагаемых значений различных параметров можно рассчитать либо мощность статистики, либо величину статистического эффекта, либо размер выборки. В дальнейших примерах мы рассмотрим две наиболее типичных ситуации, встречающиеся в исследовательской практике. Это, во-первых, расчет примерного размера выборки при планировании исследования, а во-вторых – оценка мощности уже проведенного эмпирического исследования.
PA.2 Практические примеры.
Ручной расчёт при анализе мощности требует использования специальных таблиц, в которых можно найти значение мощности статистики или размер выборки при заданных параметрах. Такие таблицы для наиболее распространенных методов можно найти, например, в книге Cohen J. Statistical power analysis for the behavioral sciences. – Routledge, 2013 (https://doi.org/10.4324/9780203771587). В настоящее время на практике для анализа мощности используются либо специальные программы, либо онлайновые калькуляторы, которые достаточно легко найти с помощью поисковых систем. Мы рассмотрим возможности Jamovi, в котором есть модуль jpower, позволяющий провести анализ мощности для различных видов t-критерия, библиотеку pwr в R, а также специализированную программу G*Power, специально разработанную для анализа мощности в самых разных случаях.
Пример PA.2(1). Расчет размера выборки в случае сравнения двух независимых выборок
Рассмотрим следующую ситуацию: исследователь планирует проанализировать гендерные различия удовлетворенностью жизнью у подростков. В качестве инструмента для измерения удовлетворенности жизнью он намерен использовать краткую шкалу удовлетворенности жизнью (satisfaction with life scale (SWLS), см.: Diener E., Emmons R.A., Larsen R.J., et al. The Satisfaction with Life Scale // Journal of Personality Assessment. 1985. Vol. 49 (1). P. 71—75; Осин Е.Н., Леонтьев Д.А. Краткие русскоязычные шкалы диагностики субъективного благополучия: психометрические характеристики и сравнительный анализ // Мониторинг общественного мнения: экономические и социальные перемены. 2020. № 1. С. 117—142). Анализ существующей литературы по данной тематике показывает противоречивость получаемых результатов – в ряде исследований получены свидетельства в пользу различий в уровне удовлетворенности у юношей и девушек, в других различий не обнаружено (см., например, Emerson S. D., Guhn M., Gadermann A. M. Measurement invariance of the Satisfaction with Life Scale: Reviewing three decades of research //Quality of Life Research. – 2017. – Т. 26. – №. 9. – С. 2251-2264).
Опираясь на частные исследования, проведенные в разных странах, можно предположить, что в случае различий этот эффект будет маленьким. Так, например на выборке норвежских подростков значимое различие между юношами и девушками с точки зрения размера статистического эффекта было небольшим – коэффициент d Коэна составил 0.28 (Moksnes U. K. et al. Satisfaction with life scale in adolescents: Evaluation of factor structure and gender invariance in a Norwegian sample //Social Indicators Research. – 2014. – Т. 118. – №. 2. – С. 657-671 ). Исходя из этого предварительного анализа, исследователь решает установить ожидаемый размер эффекта минимальным – 0.2, уровень значимости – стандартный – 0.05. Уровень мощности, которого исследователь хочет достичь – 0.80 (то есть, он допускает вероятность ошибки второго рода – 0.2) [4]. Таким образом, исходные данные для расчета минимального требуемого размера выборки для обнаружения этого эффекта таковы:
— Используется двусторонний t-критерий Стьюдента (нет предварительных предположений о том, что юноши более удовлетворены жизнью, чем женщины или наоборот);
- Сила эффекта – слабая — 0.2 (в терминах d Коэна);
- Уровень значимости – стандартный – 0.05;
- Требуемая мощность анализа – 0.8.
В Jamovi расчет размера выборки можно провести, если загрузить модуль jpower из библиотеки. Он пока обладает небольшим функционалом, позволяя проводить анализ мощности для трех типов t-критерия – одновыборочного, для связанных и несвязанных выборок. Выберем в соответствии с условиями вариант для независимых выборок – jpower – Independent Samples T—test. Откроется диалоговое окно, изображенное на рис. PA.2(2).
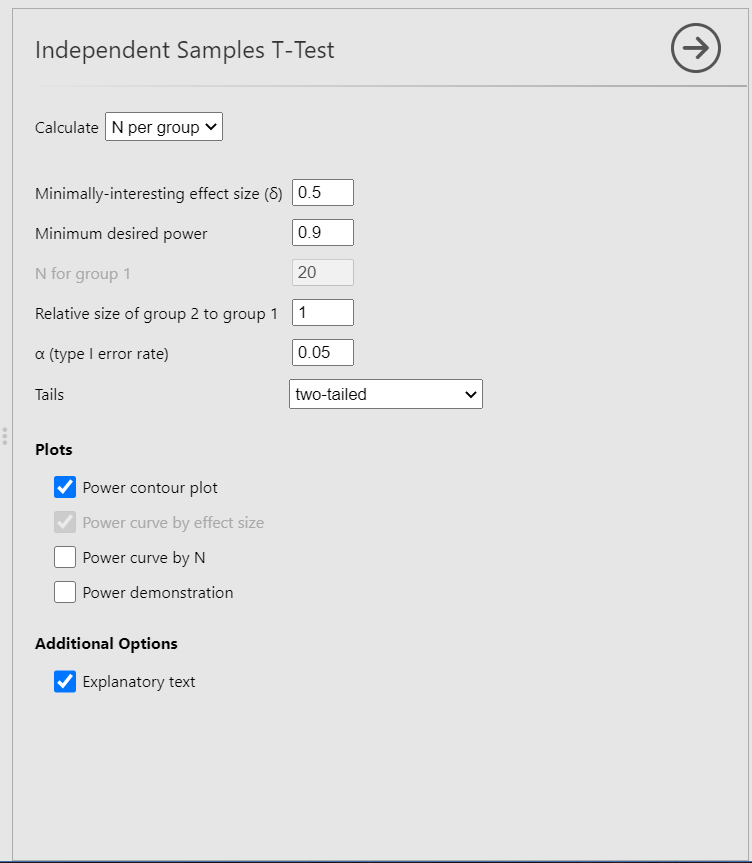 Рис. PA.2(2) Диалоговое окно проведения анализа мощности в jpower.
Рис. PA.2(2) Диалоговое окно проведения анализа мощности в jpower.
В начале можно выбрать один из типов анализа:
- N per group – расчет размера выборки (интересующий нас случай);
- Power – расчет полученной (или наблюдённой, observed) мощности для уже проведенного анализа;
- Effect size – оценка минимального эффекта при заданных размере выборки, мощности и уровня значимости.
В случае расчета размера выборки нужно указать следующие параметры:
- Minimally-interesting effect size (δ) – предполагаемый минимальный размер статистического эффекта (в случае t-критерия – это d Коэна). В нашем случае d=0.2.
- Minimum desired power – минимальная желаемая мощность анализа (то есть, уровень вероятности не совершить ошибку второго рода). Минимальная мощность, которая используется в такого рода анализе – 0.8, мы используем её.
- Relative size of group 2 to group 1 – соотношение размеров двух групп. По умолчанию предполагаются равные группы, мы используем его, но этот параметр можно при необходимости менять.
- α (type I error rate) – уровень значимости, который будет использоваться при проверке статистических гипотез (вероятность ошибки первого рода) – оставим значение по умолчанию – 0.05.
- Tails – выбор направленной(one-tailed) или ненаправленной (two-tailed) гипотезы. В нашем случае нет оснований для четких предположений о направлении различий в удовлетворенности у юношей и девушек, поэтому имеет смысл выбрать двунаправленную гипотез.
Основной результат расчета изображен на рис. PA.2(3).
 Рис. PA.2(3). Результат расчета размера выборки
Рис. PA.2(3). Результат расчета размера выборки
Как видно из таблицы, для получения значимого на уровне p<0.05 результата при таком маленьком предполагаемом эффекте, согласно проведённым расчетам, требуются достаточно большие выборки – по 394 человек в каждой группе.
Ниже можно увидеть график, отражающий размер требуемой выборки в зависимости от ожидаемого эффекта и требуемой мощности (при уровне значимости зафиксированном на 0.05), см. рис. PA.2(4). Из него можно понять, насколько меньшая или большая выборка может потребоваться для обнаружения более или менее сильного эффекта. Например, если реальный эффект окажется на уровне 1.0, то для его обнаружения при мощности 0.8 может потребоваться всего около 20 человек в каждой группе.
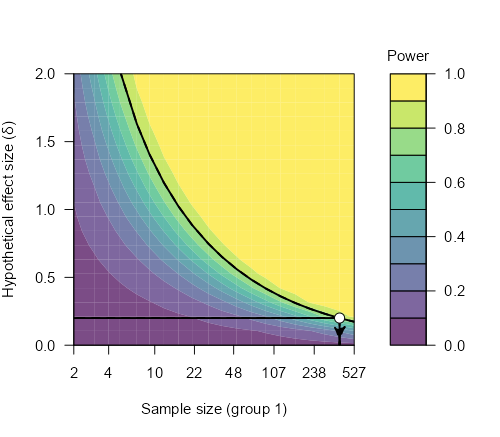 Рис. PA.2(4). График изменения размера выборки, необходимой для обнаружения более или менее сильного эффекта (Power Contour).
Рис. PA.2(4). График изменения размера выборки, необходимой для обнаружения более или менее сильного эффекта (Power Contour).
Для анализа мощности в R можно использовать различные библиотеки, мы воспользуемся одной из наиболее популярных – pwr. В начале она должна быть установлена и загружена, напоминаем соответствующие команды:
install.packages("pwr")
require(pwr)
Пакет включает в себя разнообразные функции общего вида pwr.тип.теста, с аргументами, соответствующими перечисленным выше параметрам: размер статистического эффекта, уровень значимости, размер выборки, мощность, направленность гипотез (если она возможна в критерии). В зависимости от того, какой из аргументов пропущен, функция рассчитывает именно его значение. В нашем примере следует использовать функцию pwr.t.testс аргументами d = 0.2 (размер эффекта), sig.level = 0.05 (уровень значимости), power = 0.8 (мощность) и alternative = «two.sided». Также явно укажем аргумент type = «two.sample», указывающий интересующий нас тип t-критерия (он стоит по умолчанию, при необходимости можно его изменить на «one.sample» или «paired» для работы с одновыборочным или парным t-критерием соответственно. В результате будет рассчитан размер группы:
pwr.t.test(d = 0.2, sig.level = 0.05, power = 0.8, type = "two.sample", alternative = "two.sided") Two-sample t test power calculation n = 393.4057 d = 0.2 sig.level = 0.05 power = 0.8 alternative = two.sided
Точный расчет даёт результат без округления. Что приводит к дробному значению числа испытуемых, его можно округлить (лучше вверх, до ближайшего целого). Таким образом, оказывается, что для получения значимого на уровне p<0.05 результата при таком маленьком предполагаемом эффекте требуются достаточно большие выборки – по 394 человек в каждой группе.
Пакет G*Power распространяется бесплатно, его можно скачать с сайта https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower, там же есть подробная документация и дополнительная информация. Эта программа имеет достаточно удобный графический интерфейс и предназначена для анализа мощности в самых разных ситуациях. Очень коротко опишем её интерфейс. При запуске появляется окно, изображенное на риc. PA.2(5).
 Рис. PA.2(5). Интерфейс G*Power
Рис. PA.2(5). Интерфейс G*Power
Для проведения анализа пользователь должен выбрать тип статистического теста, который он собирается использовать в поле Test Family. В G*Power предусмотрено 5 семейств тестов:
- Точные (Exact) для оценки корреляций и пропорций;
- F-отношения (F tests), используемые в дисперсионном анализе и общей линейной модели;
- T-тесты (T tests), используемые при сравнении средних в одной или двух выборках;
- Тесты хи-квадрат (χ2 tests), используемые при анализе таблиц сопряженности
- Z-тесты (Z tests), с помощью которых решаются задачи сравнения корреляций, проводится расчет тетрахорических корреляций, оцениваются логистстические регрессионные модели и т.д.
В нашем случае нужно выбрать вариант T tests.
Следующее поле (Statistical tests) позволяет выбрать конкретный вид анализа, который собирается использовать или использовал исследователь. Список этих тестов достаточно обширен, его подробное описание выходит за пределы нашего учебника, мы можем адресовать заинтересованного читателя к документации G*Power (https://www.psychologie.hhu.de/fileadmin/redaktion/Fakultaeten/Mathematisch-Naturwissenschaftliche_Fakultaet/Psychologie/AAP/gpower/GPowerManual.pdf). В семейство Т-тестов включены бисериальная корреляция, оценки коэффициентов в простой и множественной линейная регрессии, t-критерий для одной, двух несвязанных и парных выборок и их непараметрические аналоги – критерии Вилкоксона и Манна-Уитни. В соответствии с условиями задачи, выберем вариант Means: Difference between two independent means (two groups) (Средние: различие двух независимых средних (две группы).
Далее, в поле Type of power analysis можно выбрать один из пяти вариантов анализа:
- Расчет минимального размера выборки для заданного размера эффекта, уровня значимости и мощности (A priori: Compute required sample size — given α, power, and effect size). Именно этот вариант нам нужен в рамках данной задачи.
- Расчет уровня значимости и мощности при заданных размере выборки, рамере эффекта и отношения вероятности двух типов ошибок (β/α) (Compromise: Compute implied α & power — given β/α ratio, sample size, and effect size). Этот тип анализа используется довольно редко и мы не будем здесь на нём останавливаться.
- Расчёт уровня значимости для заданных мощности, размера эффекта и размера выборки (Criterion: Compute required α — given power, effect size, and sample size). Это также достаточно редко используемый анализ, он может дать ориентир, какую значимость критерия можно считать убедительной для отвержения нулевой гипотезы с учетом желаемой мощности анализа.
- Расчет полученной (наблюденной) мощности на основе проведенного анализа выборочных данных и полученных значимости и размере эффекта на выборке фиксированного размера (Post hoc: Compute achieved power — given a, sample size, and effect size). Этот вариант анализа рассмотрен подробнее ниже, в примере
- Расчет требуемого размера эффекта, который будет значим при заданных мощности, уровне значимости и размере выборки (Sensitivity: Compute required effect size — given a, power, and sample size). Этот вариант анализа мы также в рамках нашего краткого введения в анализ мощности не обсуждаем, так как он используется редко.
Компактно эти виды анализа и исходные/рассчитываемые параметры изображены в таблице PA.2(6)
Таблица PA.2(6). Типы анализа мощности в G*Power.
| Размер выборки | Уровень значимости | Мощность | Отношение β/α | Размер эффекта | ||
| 1 | A priori: Compute required sample size — given α, power, and effect size | ? | + | + | — | + |
| 2 | Compromise: Compute implied α & power — given β/α ratio, sample size, and effect size | + | ? | ? | + | + |
| 3 | Criterion: Compute required α — given power, effect size, and sample size | + | ? | + | — | + |
| 4 | Post hoc: Compute achieved power — given a, sample size, and effect size | + | + | ? | — | + |
| 5 | Sensitivity: Compute required effect size — given a, power, and sample size | + | + | + | — | ? |
Примечание: «?» — рассчитываемый параметр, «+» задаваемые параметр, «-» — не используемый параметр
Выбрав вариант A priori: Compute required sample size — given α, power, and effect size, заполним необходимые поля в соответствии с условиями задачи:
- Tail(s) («хвосты», определяющие направленность гипотезы) – two (двусторонние);
- Effect size d (размер эффекта d) – равно 0.2;
- α err prob (вероятность ошибки α — уровень значимости) – 0.05;
- Power (1-0 err prob) (вероятность 1 — вероятность ошибки β, мощность)- 0.80;
- Allocation ratio N2/N1 (соотношение размеров двух групп) – по умолчанию равно 1, оставим такой вариант.
После этого нажмём кнопку Calculate и получим результат, изображенный на рис. PA.2(7).
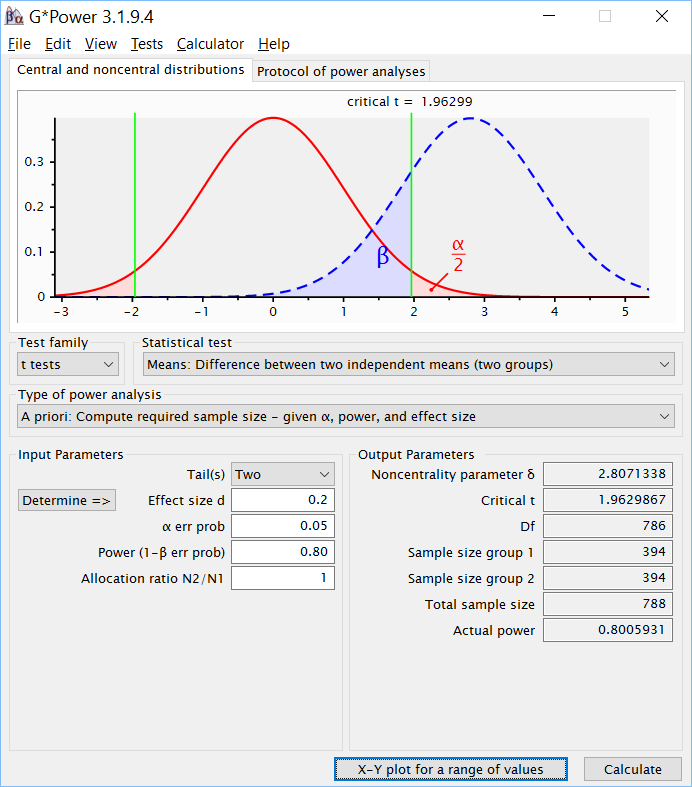 Рис. PA.2(7). Результат расчета размера выборки в G*Power.
Рис. PA.2(7). Результат расчета размера выборки в G*Power.
В разделе Output parameters приведены параметр нецентральности, критическое значение t-критерия для заданного уровня значимости, число степеней свободы и, собственно, интересующие нас размеры каждой из групп (по 394 человека в каждой, всего 788 человек) и точное значение мощности такого исследования. Таким образом, оказывается, что для получения значимого на уровне p < 0.05 результата при таком слабом эффекте и вероятности ошибки второго рода равной 0.2 минимально рекомендуемый размер выборки – почти 400 человек в каждой группе.
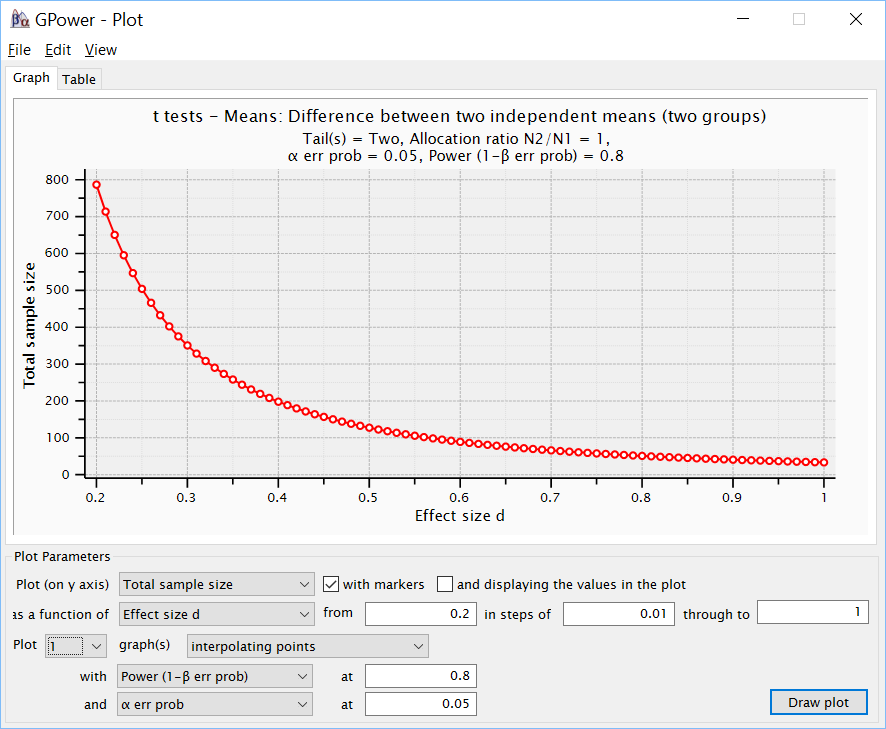
Обратим также внимание на возможность построения графиков, которые позволяют получить более полную картину об изменении интересующих исследователя показателей. Если нажать на кнопку X—Y plot for a range of values (X-Y график для набора значений), можно, например, получить график изменения размера выборки в зависимости от желаемой мощности при заданных силе эффекта и значимости или в зависимости от предполагаемого размера эффекта при заданных мощности и уровне значимости и т.п., в различных сочетаниях. Построим последний упомянутый график, для этого в поле Plot (on y axis) выберем вариант Total sample size, в поле as a function of – вариант effect size d, далее установим границы значений d – от (from) 0.1 до (to) 1 с шагом (in steps of) 0.01. Значение мощности и уровня значимости оставим тем же, что загрузились из предыдущего расчёта – 0.8 и 0.05 соответственно. Полученный график изображен на рис. PA.2(8).
Рис. PA.2(8). График изменения требуемого размера выборки в зависимости от предполагаемой силы эффекта.
Как видно из рисунка, при увеличении предполагаемого эффекта он может быть обнаружен как значимый на выборе все меньшего размера и, например, при d=0.6, общий размер выборки составляет уже чуть меньше 100, то есть меньше 50 человек в каждой группе. Точные значения можно посмотреть на вкладке Table, при d = 0.6, N = 89.1716 (округлим до 90).
Упражнение PA.2(9). Мы предлагаем читателю предположить, как изменится рекомендуемый размер выборки (уменьшится или увеличится) при:
- Увеличении минимального ожидаемого размера эффекта до 0.8.
- Увеличении мощности до 0.95.
- Снижении уровня значимости до 01.
Проведите соответствующие расчёты в jpower, R или G*Power и проверьте свои предположения.
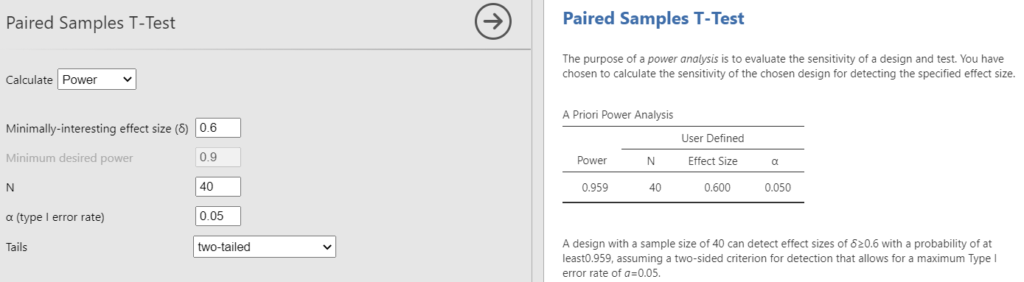
Упражнение PA.2(10). Расчет размера выборки для оценки различий в парных выборках.
Исследователь планирует оценить эффективность тренинга коммуникативных способностей. Он предварительно полагает, что тренинг может иметь средний эффект (по крайней мере d=0.6)[5]. Уровень значимости он планирует использовать стандартный — 0.05, а мощность исследования хотел бы получить достаточно высокую – 0.95. С помощью Jamovi, пакета pwr в R или G*Power рассчитайте минимальный требуемый в этих условиях размер выборки испытуемых.
Ответ для самопроверки: N = 39 при двусторонней или N=32 при односторонней гипотезе.
Пример PA.2(11). Оценка мощности, полученной в проведенном исследовании (post hoc).
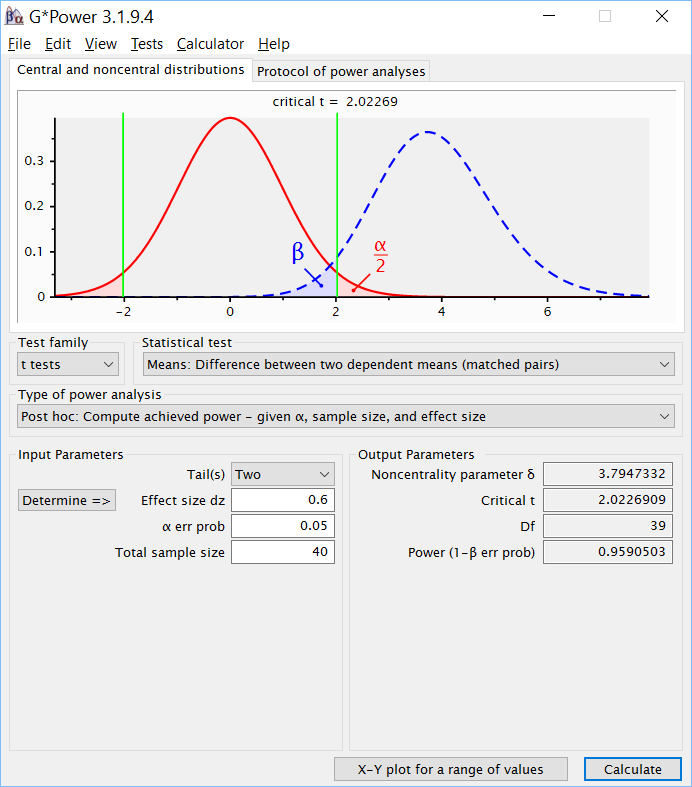
Решим обратную задачу – расчет мощности проведенного исследования. Допустим, исследователь сравнил с помощью t-критерия Стьюдента уровень тревожности в небольшой выборке студентов размером в 40 человек в начале и в конце учебного семестра. Уровень значимости, который он использовал был стандартным – 0.05, размер обнаруженного эффекта d= 0.6. Какова мощность полученного результата и как можно проинтерпретировать эту мощность? Сначала опишем техническое решение в разных программных пакетах, а затем остановимся на его смысле.
Используем уже знакомую нам функцию pwr.t.test из пакета pwr, указав аргументы, соответствующие условию: d (размер эффекта), n (размер выборки), sig.level (уровень значимости) и тип теста – paired (парный):
pwr.t.test(d = 0.6, sig.level = 0.05, n = 40, type = "paired", alternative = "two.sided") Paired t test power calculation n = 40 d = 0.6 sig.level = 0.05 power = 0.9590503 alternative = two.sided NOTE: n is number of *pairs*
Таким образом, полученная мощность оказывается равной 0.9590503
Выберем test family – t tests, Statistical test – Means: Difference between two dependent means (matched pairs) и Type of power analysis — Post hoc: Compute achieved power — given a, sample size, and effect size. Затем введем указанные в условии размер эффекта (d Коэна), уровень значимости и размер выборки. Полученный результата показывает. Что полученная мощность анализа составляет 0.959:
Теперь остановимся на важном вопросе – что означает полученная мощность, как её интерпретировать? Напомним, что мощность определяется как вероятность не совершить ошибку второго рода, то есть, можно сказать – вероятность не пропустить реально существующий эффект. Когда исследование уже проведено и результат получен, эффект оценён, то к этому коэффициенту можно отнестись как к ориентиру воспроизводимости этого эффекта в последующих исследованиях. Если полученная в нашем исследовании оценка эффекта отражает реальное положение вещей, то оценка мощности показывает вероятность его воспроизвести, не совершив ошибку второго рода, на выборке такого же размера в аналогичном исследовании[6]. Насколько такая оценка важна и стоит подробного обсуждения – дискуссионный вопрос. Заметим в связи с этим, что на практике такой анализ проводится довольно редко. Гораздо чаще в настоящее время используется оценка требуемого размера выборки – это помогает планировать исследования в целом и становится особенно важным в случае предварительной регистрации исследований.
В заключении раздела приведем еще несколько коротких примеров оценок размера выборок для двух распространенных статистических критериев – коэффициента корреляции Пирсона и F-отношения в дисперсионном анализе.
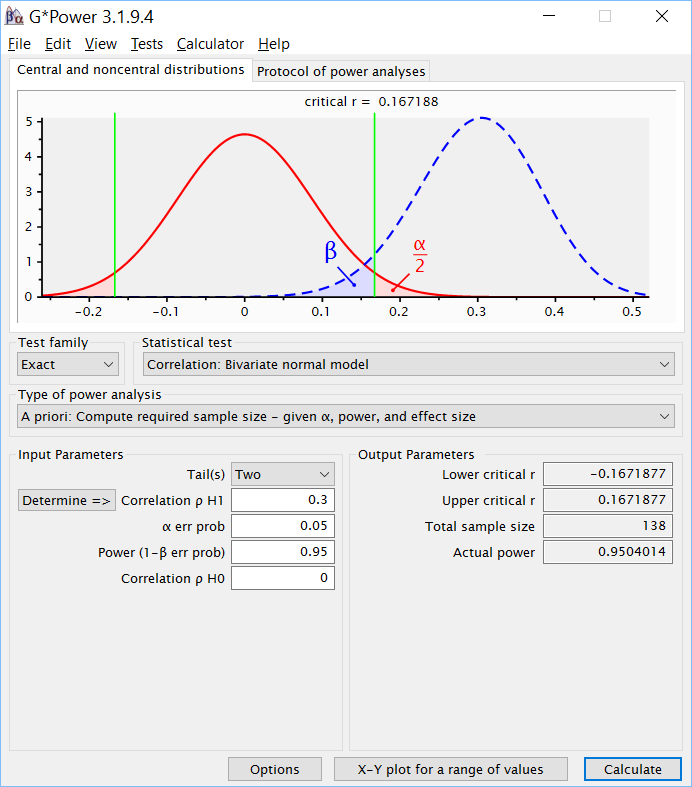
Пример PA.2(13). Оценка размера выборки для корреляционного исследования.
Допустим, исследователь хочет рассчитать корреляцию между уровнем удовлетворенности жизнью и уровнем оптимизма. Он, не анализируя литературу, просто рассчитывает на достаточно распространенное значение корреляции между психологическими параметрами – 0.3, использует стандартный уровень значимости – 0.05 и хочет получить мощность 0.95. Каков должен быть минимальный размер выборки в этих условиях? В Jamovi такой анализ провести пока что нельзя, поэтому опишем решение в R и G*Power.
Для расчета размера выборки для корреляций можно использовать функцию pwr.r.testиз пакета pwr. Аргументы функции заполняются в соответствии с условием: r = 0.3, sig.level = 0.05, power = 0.95:
pwr.r.test(r = 0.3, sig.level = 0.05, power = 0.95) approximate correlation power calculation (arctangh transformation) n = 137.7587 r = 0.3 sig.level = 0.05 power = 0.95 alternative = two.sided
Минимальный размер выборки – 138 человек (с учетом округления вверх)
Для проведения расчета требуемой выборки в G*Power надо выбрать Test family – Exact, Statistical test – Bivariate normal model и Type of power analysis – A priori: Compute required sample size — given α, power, and effect size, выбрать двустороннюю гипотезу (Tails – two), а затем ввести указанные в условия параметры – Correlation ρ H1 – 0.3, α – 0.05, Power – 0.95. Отметим, что можно также произвольно указать и корреляцию, соответствующую нулевой гипотезы, но в данном случае нет оснований устанавливать её отличной от нуля. В результате оценка требуемого размера выборки составит 138 испытуемых (см. рис. PA.2(14)).
Рис. PA.2(14). Оценка размера выборки в корреляционном исследовании
Пример PA.2(15). Оценка размера выборки в дисперсионном анализе.
Исследователь планирует оценить уровень депрессии в группах больных с различными типами психических заболеваний – больных, страдающих обсессивно-компульсивным расстройством, шизофреников, и людьми с расстройством пищевого поведения – в сравнении с группой нормы. Предполагаемый эффект он оценивает как невысокий, в терминах знакомого нам из раздела 7.3 коэффициента η2 равного 0.1, планирует использовать уровень значимости 0.05 и желаемую мощность устанавливает на уровне 0.9. Требуется рассчитать требуемый размер выборки для получения значимого эффекта в таких условиях. Также как в случае корреляции в предыдущем примере такой анализ нельзя провести в Jamovi, но можно в R и G*Power. Однако, прежде, чем описать как это можно сделать, остановимся на одной технической детали. В качестве коэффициента размера статистического эффекта в обоих пакетах используется не η2, а коэффициент f, рассчитываемый как отношение стандартного отклонения средних сравниваемых групп к общему стандартному внутригрупповому стандартному отклонению. Этот коэффициент пересчитывается из η2 по формуле \( f=\sqrt{(η^2/(1-η^2))} \). Таким образом, в нашем случае \( f = \sqrt{(.1/.9)}=.33(3) \) [7][/simple_tooltip].
В пакете pwr есть функция pwr.anova.test, позволяющая провести анализ мощности для дисперсионного анализа. В нашем случае необходимо указать значения аргументов k = 4 (число уровне фактора или групп), f = 0.333, sig.level = 0.05, power=0.9:
pwr.anova.test(k = 4, f = 0.333, sig.level = 0.05, power=0.9) Balanced one-way analysis of variance power calculation k = 4 n = 32.94472 f = 0.333 sig.level = 0.05 power = 0.9 NOTE: n is number in each group
Как видно из результата расчетов, требуемый размер каждой из групп – 33 человека (с учётом округления)[8].
Для проведения расчета требуемой выборки в G*Power надо выбрать Test family – F test, Statistical test – ANOVA: Fixed effects, omnibus, one-way и Type of power analysis – A priori: Compute required sample size — given α, power, and effect size, а затем ввести указанные в условия параметры – f – 0.333, α – 0.05, Power – 0.9 и Number of groups – 4. В результате оценка требуемого размера всей выборки составит 132 испытуемых, то есть 33 человека в каждой группе (см. рис. PA.2(16)).
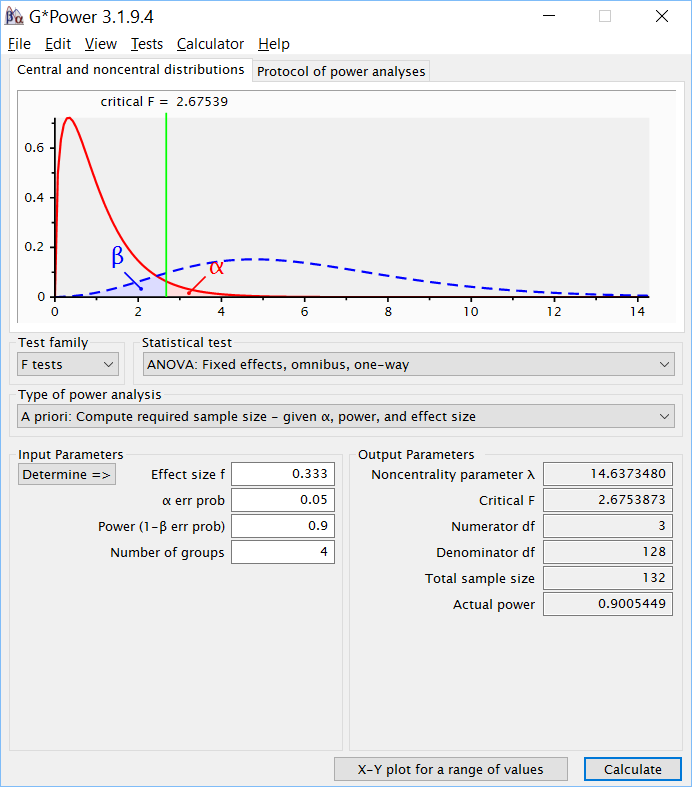 Рис. PA.2(16). Оценка размера выборки для однофакторного дисперсионного анализа
Рис. PA.2(16). Оценка размера выборки для однофакторного дисперсионного анализа
[1] Интересный вопрос – может ли быть объём выборки «слишком большим»? При увеличении выборки с учётом особенностей генеральной совокупности (например, соблюдение её половой и возрастной структуры и т.п.) её репрезентативность повышается. Также растёт мощность выборки – то есть, вероятность избежать ошибку второго рода, а также повышается чувствительность статистики (все меньшее значение статистик могут быть оценены как значимые). Таким образом, увеличение выборки выглядит как положительный фактор, позволяющий получить более точный результат. Однако, при работе с большими выборками нужно быть осторожными с точки зрения интерпретации получаемых эффектов и их практической или содержательной «значимости». На больших выборках легко получить значимый результат при минимальном размере эффекта, поэтому в этих случаях особенно важно дополнять данные о полученной значимости коэффициентами статистического эффекта.
[2] Заметим также, что эффект в первом случае равен 0, а во втором – \( d=\frac{1}{4}=0.25 \, что считается слабым эффектом.
[3] Подробное рассмотрение нецентрального распределения Стьюдента выходит за пределы этого небольшого введения в анализ мощности, но укажем, что оно в отличие от стандартного распределения Стьюдента, асимметрично и описывает распределение t-статистики в случае, когда его математическое ожидание смещено относительно нуля (см. подробнее https://ru.qaz.wiki/wiki/Noncentral_t-distribution, https://scask.ru/m_book_prs1.php?id=35)
[4] Обратим внимание читателя, что такой подход требует дополнительной содержательной работы – обзора имеющихся исследований по соответствующей тематике, учета уже полученных в других работах данных и т.п. При этом чем конкретнее план исследования, тем проще формулировать такие априорные предположения, ориентируясь на конкретные измерительные процедуры и методики.
[5] Заметим, что в данном случае можно рассуждать и так: более слабый эффект тренинга неинтересен, поэтому если он не будет оценен как значимый (будет совершена ошибка второго рода из-за малой эффективности тренинга) – это будет в некотором смысле адекватно.
[6] При этом надо помнить о том, что при истинной нулевой гипотезе мы можем получить случайно заметный эффект и совершить ошибку первого рода – в таком случае расчёт мощности технически возможен, но содержательно бессмысленен, как и разговоры о воспризводимости этой ошибки, естественно.
[7] В G*Power есть калькулятор, позволяющий сделать этот пересчет без обращения к формуле.
[8] Расчет в данном случае проводится для равных по размеру групп.