5.1.1. Стандартное отклонение как единица измерения индивидуального результата
Рост голландского футболиста Робина ван Перси 183 см. Для расчета высоты дверных проемов в строящейся квартире этого достаточно. Для ответа на вопрос, высок ли Робин или нет, у нас нет достаточной информации. Если мы узнаем, что средний рост мужчины-европейца в настоящее время равен 178 см, то мы сможем сказать, что рост ван Перси выше среднего. Если мы найдем информацию о том, что стандартное отклонение роста мужчин по всей генеральной совокупности мужчин-европейцев равно 5 см, то получим уже довольно ясное представление о месте ван Перси в распределении ростов. А именно, рассматривая это распределение как приблизительно нормальное, мы видим, что рост ван Перси отклоняется от среднего европейского на 5 см, т.е. ровно на одно стандартное отклонение. По таблице 4.1.3(2) единице отклонения в стандартном нормальном распределении соответствует вероятность 0.341. Это значит, что ниже ван Перси оказывается примерно \( 0.5+0.341=0.841 (84.1\%) \) европейского мужского населения, а выше него примерно \( 0.159 (15.9\%) \) мужчин-европейцев. Оба показателя равно информативны: можно сказать, что Z-оценка (Z-score) роста ван Перси равна 1, можно сказать, что рост ван Перси отсекает от распределения верхний «хвост» весом в 0.159.
Однако среднее 178 и стандартное отклонение 5 в данном случае, как и практически всегда в подобных случаях, не были получены измерением всех европейцев, а были оценены по выборкам. Предположим, мы хотим оценить средний рост жителей какого-то достаточно большого города, например Томска. Мы набираем случайную выборку из взрослых мужчин-томичей объемом 100 человек. Поскольку мы не знаем не только средний рост томичей, но и стандартное отклонение распределения в генеральной совокупности, мы оцениваем оба показателя по выборке.
5.1.2. Стандартная ошибка как единица измерения точности оценки по выборке
Пусть \( \overline{x}=177 \), а оцененное по выборке стандартное отклонение \( s=4 \). Как всегда в таких случаях, мы можем быть уверены, что полученный результат \( \overline{x}=177 \) не совпадает в точности со средним ростом томичей, а лишь более или менее близок к нему. Опираясь на оценки среднего и дисперсии, которые дает наша выборка, мы построим доверительный интервал для среднего, т.е. определим промежуток возможных значений неизвестного среднего роста томичей, которые согласуются с нашей выборкой.
Определение 5.1.2(1). Для выборки объема n cтандартной ошибкой среднего (обозначается se) называется выборочное стандартное отклонение, деленное на \( \sqrt{n} \):
\[ se=\frac{s_x}{\sqrt{n}} \]
Деление на \( \sqrt{n} \) вытекает из теорем о дисперсии третьей главы. Здесь мы даем только алгоритм вычисления доверительного интервала, дальнейшие разъяснения в следующем параграфе.
Доверительный интервал среднего — это наглядное представление возможных значений оцениваемого настоящего математического ожидания, которые в определенной степени согласуются с полученным результатом. Степень согласованности выражается в процентах. Можно сказать так: ноль-процентный доверительный интервал — это в точности выборочное среднее, а стопроцентный — вся числовая ось, поскольку абсолютно достоверно мы можем утверждать лишь, что настоящее математическое ожидание лежит где-то на числовой оси. Обычно используются 95 и 99 процентов степени согласованности. Доверительный интервал легко построить, но точный смысл его не так прост. Мы обсудим это в параграфе 5.2.
Радиус 95-процентного доверительного интервала для среднего вычисляется умножением стандартной ошибки se, в нашем случае равной \( 4/\sqrt{100}=0.4 \), на число 1.96, полученное из таблицы нормального распределения (интервал (-1.96; 1.96) вырезает 95% площади под кривой стандартного нормального распределения).
Доверительный интервал среднего по данной выборке получается откладыванием радиуса в обе стороны от выборочного среднего. В результате получим интервал радиуса с центром в 177, т.е. (176.22; 177.78). Нам тем самым даны границы: если реальный средний рост томичей лежит в данном интервале, то в появлении результата 177 (при объеме выборки 100) нет ничего удивительного, результат 177 согласуется с любым из значений из этого интервала. Значения среднего роста томичей вне этого интервала менее правдоподобны, и чем дальше от границ вовне, тем они согласуются с результатом 177 меньше.
Замечание 5.1.2(2). Мы рассчитывали доверительные границы по таблице нормального распределения. Здесь необходимо уточнить, что для выборок объема n<100 (и чем меньше выборка, тем это существеннее) доверительные границы следует рассчитывать с помощью таблиц распределения Стьюдента (Student’s t-distribution) с n−1 степенью свободы. По сравнению с нормальным распределением, распределение Стьюдента имеет несколько более тяжелые хвосты [1] и они тем тяжелее, чем меньше объем выборки, поэтому границы доверительных интервалов оказываются тем шире, по сравнению с вычисленными по нормальным таблицам, чем меньше n. Для n=100 различия распределений Стьюдента и нормального почти незаметны (рис. 5.1.3(2)).
5.1.3. Определения основных понятий. Одновыборочный T-критерий (Стьюдента)
Мы уже фактически использовали квантили распределений, не называя их. Теперь мы дадим определение.
Определение 5.1.3(1). Пусть задано распределение некой случайной величины, и это распределение симметрично относительно нуля. Двухсторонний квантиль уровня α данного распределения это пара чисел (оно называется нижний двухсторонний квантиль) и (оно называется верхний двухсторонний квантиль) [3], таких, что вероятность попадания данной случайной величины в интервал между нижним и верхним квантилями или, что одно и то же, площадь под кривой плотности распределения между нижним и верхним квантилями равна 1 − α.
Например, -1.96 и 1.96 — нижний и верхний двухсторонние квантили стандартного нормального распределения на уровне 0.05. Такие квантили называют еще 5%-й. Для краткости будем говорить: 1.96 — 5%-й двухсторонний квантиль нормального распределения, подразумевая, что это верхний двухсторонний квантиль, а нижний имеет симметричное отрицательное значение.
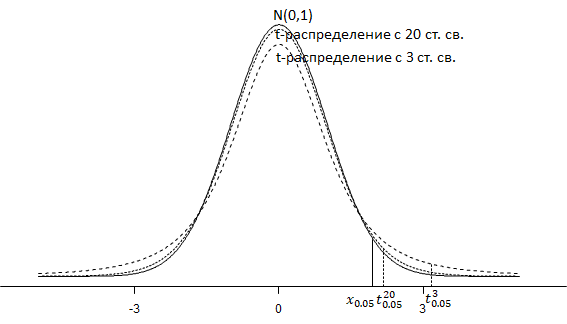
Как мы уже говорили, у распределения Стьюдента более тяжелые хвосты, поэтому для выборки объема 21 двухсторонний 5%-й квантиль для распределения Стьюдента с 20 степенями свободы [4] это 2.08, а для 3 степеней свободы (для выборки объема 4) — 3.18 (рис. 5.1.3(2)). При уменьшении числа степеней свободы графики распределения Стьюдента «уплощаются», а квантили монотонно удаляются от начала координат.
Рис. 5.1.3(2). Графики стандартного нормального распределения и t-распределений (Стьюдента) с 20 и 3 степенями свободы; \( x_{0.05}=1.96 \) — верхний двухсторонний 5%-й квантиль нормального распределения, \( t^{20}_{0.05}=2.08 \) — верхний двухсторонний 5%-й квантиль t-распределения с 20 степенями свободы, \( t^{3}_{0.05}=3.18 \) — верхний двухсторонний 5%-й квантиль t-распределения с 3 степенями свободы.
Для построения 95%-ых и 99%-ых доверительных интервалов мы берем соответствующие квантили соответствующих распределений.
Можно решить обратную задачу. Если мы имеем ориентированный на данное распределение результат (пока подразумеваем распределение Стьюдента, совпадающее в пределе с нормальным, далее мы рассмотрим и другие полезные распределения), то мы можем оценить этот результат удвоенным весом отсекаемого им хвоста распределения. Вернемся к первому примеру предыдущего пункта. Если мы хотим оценить соответствие гипотезы «средний рост жителей Томска 178 сантиметров» полученному выборочному среднему 177 см по описанной выше выборке объема 100, то следует поделить абсолютную величину [5] разности 178 − 177 на стандартную ошибку, равную 0.4. Получив результат 2.5, мы можем оценить по таблице нормального распределения вес верхнего хвоста — по таблице это , вес двух симметричных хвостов 0.012.
Определение 5.1.3(3). Так рассчитанный вес отсекаемых данным результатом хвостов называется значимостью этого результата относительно данной гипотезы. Можно также называть это число значимостью гипотезы относительно результата или значимостью различия полученного результата и гипотезы. Чем меньше вес отсекаемых хвостов, тем больше у нас оснований считать не случайным отклонение полученного результата от значения, заданного гипотезой.
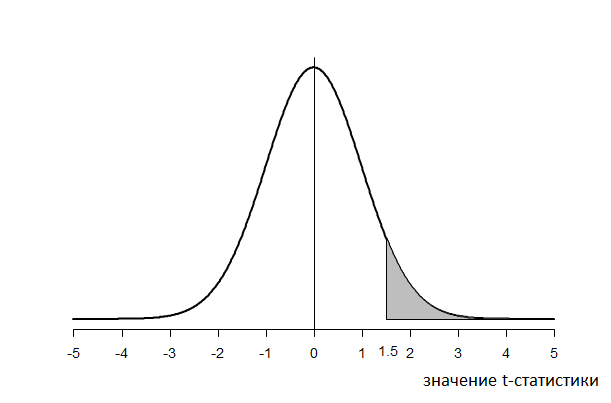
Еще раз вернемся к примеру подпараграфа 5.1.2. Каждая гипотеза оценивается своей значимостью по отношению к полученному нами результату (среднее 177 при стандартном отклонении 4 на выборке 100 человек). Для гипотезы «средний рост томичей равен 176.4» разность, измеренная стандартной ошибкой 0.4, дает результат . Взяв модуль результата 1.5, рассмотрим верхний хвост (рис. 5.1.3(4)), площадь которого определим по таблице 4.1.3(2) стандартного нормального распределения. Она равна \( 0.5-0.433=0.076 \). Удвоив, получаем \( 0.134 \). Это значимость, соответствующая гипотезе «средний рост томичей равен 176.4» по отношению к результату 177 со стандартным отклонением 4 по выборке объема 100.
Рис. 5.1.3(4). Оценка значимости результата «среднее выборочное равно 177» по выборке объема 100 со стандартным отклонением 4 относительно гипотезы «среднее по генеральной совокупности равно 176.4». Статистика \( t=(177-176.4)/0.4=1.5 \). Хвост, отсекаемый значением 1.5 под стандартным нормальным распределением, имеет площадь 0.067. Значимость равна \( 0.067*2=0.134 \).
95%-й доверительный интервал накрывает в нашем случае гипотезы, значимость которых по отношению к этому результату выражается числами, превосходящими \( 1 − 0.95 = 0.05 \).
Посмотрим теперь, что произойдет, если объем выборки увеличить до 400. Предположим, что среднее выборочное и стандартное отклонение остались теми же (в реальности они, конечно, изменились бы, но, скорее всего, не существенно). Новые вычисления дали бы другое значение \( \sqrt{n} \), теперь \( 4/\sqrt{400}=0.2 \), и радиус доверительного интервала становится вдвое меньше. Гипотезе «средний рост томичей равен 178» соответствует вдвое большее, чем по выборке объема 100, Z-значение отклонения, оно теперь равно 5. Значимость (вес соответствующих хвостов) для отклонения 5 меньше 0.000001 (в нашем распоряжении нет таблиц, которые бы точно оценили вероятности для таких больших отклонений, но эти вероятности легко рассчитать с помощью специализированных программ или на общедоступных сайтах).
Техника построения доверительных интервалов и оценки значимости, которую мы здесь разобрали, называется Т-критерием [2] или критерием Стьюдента. Итак, в общем случае для выборки объема n в задачах, подобных разобранной выше, для построения доверительных интервалов и оценки значимости сначала вычисляется стандартная ошибка se. Затем берется двухсторонний квантиль (5%-й для 95%-го доверительного интервала, 1%-й для 99%-го) распределения Стьюдента с степенями свободы (вручную это можно сделать с помощью таблиц, SPSS вычисляет его самостоятельно). Радиус R соответствующего доверительного интервала получается умножением квантиля на стандартную ошибку. Сам доверительный интервал — это промежуток \( (\overline{x}-R;\overline{x}+R) \). Он дает представление о диапазоне согласующихся с полученной выборкой на соответствующем уровне доверия (95, 99%-м или ином) вариантов гипотетического среднего в генеральной совокупности.
Операция оценки значимости такова: разность выборочного среднего и проверяемого гипотетического среднего делится на стандартную ошибку. Результат \( t=(\overline{x}-a)/se \) называется значением t-статистики. Значимость определяется так: абсолютная величина t откладывается по оси абсцисс графика распределения Стьюдента с соответствующим числом степеней свободы. Затем вычисляется площадь верхнего хвоста распределения, отсекаемого этим значением. Удвоенная площадь хвоста и объявляется значимостью результата относительно данной гипотезы.
Приведем в заключение рецепт вычисления t-статистики в виде формулы:
\[ t=\frac{\overline{x}-a}{se}= \frac{\overline{x}-a}{\sqrt{\frac{1}{n-1}\sum{(x-\overline{x})^2}}}\cdot\sqrt{n}. \]
Знак суммы здесь и везде далее подразумевает суммирование по всем элементам выборки.
5.1.4. Значимость 0.05 как социально закрепленная граница принятия решения в психологии
В исследовательской практике и в обычаях принятия результатов к публикации значимость 0.05 служит границей принятия решения. Если гипотеза имеет значимость по отношению к данной выборке меньше или равную 0.05, то она считается отвергнутой как маловероятная при полученных результатах, если больше 0.05, то не отвергнутой.
В значительном числе исследовательских ситуаций одна из гипотез выделена как наиболее важная опорная точка. Например, в исследовании подпараграфа 5.1.2 нас интересовало, меньше или не меньше рост томичей, чем рост европейцев. Гипотеза «Средний рост томичей равен среднему росту европейцев» выделяется среди других, обозначается и называется нулевой гипотезой или нуль-гипотезой.
Наиболее часто исследование, связанное со сравнением средних, строится именно так: формулируется нулевая гипотеза (о равенстве среднего какому-то числу или равенстве двух средних), формулируется альтернативная гипотеза (одно среднее больше другого и т.п. или просто «средние не равны») и предполагается, что в случае, если значимость нулевой гипотезы по отношению к полученной выборке меньше 0.05 (это значит, что разность средних достаточно велика — она превосходит приблизительно две стандартные ошибки), будет принята альтернатива, если больше 0.05 (разность средних невелика) — будет принята нулевая гипотеза о равенстве. Обычно интересным научным результатом оказывается как раз альтернативная гипотеза «голландцы выше средних европейцев», или «тренинг оптимизма в среднем увеличивает оптимизм участников», или «опосредствование запоминания слов карточками увеличивает количество воспроизведенных слов», и результат в таком случае формулируется, например, так: принимается (альтернативная) гипотеза на уровне значимости [6] 0.019. Это означает только, что значимость нулевой гипотезы («голландцы не выше средних европейцев», или «тренинг оптимизма в среднем не увеличивает оптимизм участников», или «опосредствование запоминания слов карточками не увеличивает количество воспроизведенных слов») по отношению к выборке равна 0.019, или, что почти то же самое, 98%-й доверительный интервал не включает нулевое значение, а 99%-й уже включает.
Если задача стоит так, что мы должны принять одну из гипотез, то тогда необходимо заранее договориться о том, какая значимость гипотезы \( H_0 \) по отношению к полученной выборке будет говорить в ее пользу. Как мы говорили, в настоящее время принято считать такой границей 0.05. Большинство журналов в России [7] принимает статьи, в которых значимость нулевой гипотезы (\( H_0 \) ) меньше 0.05, и она отвергается в пользу интересующей автора альтернативной гипотезы . Если мы принимаем такое условие выбора (равно как и любое другое), то нам грозят естественные ошибки: отвергнуть \( H_0 \), когда она верна, и принять ее, когда она не верна.
Определение 5.1.4(1). Ошибкой первого рода называется отвержение \( H_0 \), когда она верна. Ошибкой второго рода называется принятие \( H_0 \), когда она не верна.
Например, наши стандартные 0.05 оказываются при таком правиле принятия решения вероятностью ошибки первого рода. Для единственного эксперимента это означает следующее: мы выбираем такой уровень значимости (0.05), что вероятность отвергнуть нуль-гипотезу, если она верна, при проведении единичного эксперимента невелика (0.05).
Однако в массовых исследованиях ситуация меняется: истинная гипотеза может быть в конце концов отвергнута, если исследователи проявят достаточное упорство. Например, гипотеза о том, что телепатии не существует, если ее примутся проверять 100 исследовательских коллективов, в которых заведомо нет телепатов, будет тем не менее отвергнута по принятому правилу примерно пятью из этих ста групп. Если остальные 95 никак не сообщат о своих результатах, то в журналах могут появиться пять статей со статистическими «доказательствами». В любом случае такие результаты науке полезны не будут.
Подобный сбой метода оценивания называется публикационный сдвиг (publication bias в англоязычной литературе, где термин был введен).
Современная тенденция решения проблемы публикационного сдвига такова:
- В том или ином виде информация о неудачных экспериментах (т.е. тех, в которых нуль-гипотеза не была отвергнута) должна быть доступна сообществу.
- Одно исследование, как правило, ничего не доказывает. Не обязательно объявлять гипотезу отвергнутой или принятой — вполне можно ограничиться более мягкими формулировками, оставив сообществу развитие темы.
- Правильнее предоставить максимально полную информацию об исследовании, которая даст возможность полностью корректно сопоставлять все исследования в данной области — удачные и неудачные. Такое сопоставление называется метаанализом и является в настоящее время очень важным инструментом исследований.
В исследованиях, связанных с оценками средних значений, для возможности мета-анализа достаточно публиковать выборочные средние, объемы выборок и стандартные отклонения. В настоящее время в различных сферах исследований создаются базы данных, где такие результаты публикуются вне зависимости от того, больше или меньше 0.05 оказываются значимости гипотез. Мы полностью на стороне этой практики.
Обратим в заключение внимание читателя на то, что статистика может предъявить практически надежное доказательство. Если значимость нулевой гипотезы равна 0.00000001, то авторы учебника готовы считать альтернативную гипотезу доказанной (в той степени, в какой в науке вообще можно что-нибудь доказать) — надо только убедиться, что экспериментальные процедуры совершенно свободны от ошибок. Нередко метаанализ доводит результаты до такой степени убедительности.
5.1.5. Статистическая значимость — не единственное, что нам нужно от результата. Другие виды значимости
Статистическая значимость результата не означает, что он содержательно значим — значим для психологической теории или практики. Например, важна ли для биолога (антропометриста) средняя разница в росте между томичами и европейцами в 0.1 см (177.9 против 178 см), даже если на наших, довольно больших, выборках она достигает уровня статистической значимости? Следует ли считать тренинг оптимизма эффективным с психологической точки зрения, если в среднем на выборке в 100 человек он привел к увеличению оптимизма в среднем на 5 баллов (по некоторой шкале), но у двух человек из этих 100 — к его ухудшению (нарастанию пессимизма) на 30 — 40 баллов (в той же шкале)? С точки зрения психолога ухудшение (хотя это и исключение) может иметь больший содержательный смысл, нежели небольшое улучшение в среднем. Делая психологический вывод из исследования на основе статистической значимости, важно дополнять его другими, нестатистическими мерами оценки значимости результатов. То, в какой степени результаты соответствуют (не противоречат) теории (или одной из теорий) или важны для решения научной проблемы, называют содержательной значимостью. Так, доказанная разница в росте в 0.1 см содержательной значимостью для практика вряд ли обладает. Наоборот, если задача исследователя — сравнить в эксперименте предсказания двух альтернативных теорий, результаты, согласующиеся с одной из них и противоречащие другой, даже если они не подтверждаются статистикой вполне убедительно, — важная пища для размышлений. Возможно, продолжив эксперимент или видоизменив его, психолог сможет достичь более сильного статистического подтверждения своих предположений.
Важность результатов для какой-либо области практики называют практической значимостью (в медицине и клинической психологии ее обозначают как клиническую значимость). Например, если по итогам специальной программы обучения детей коррекционного класса несколько из них показали результаты, которые позволили им учиться в общеобразовательной школе, эффект программы может быть значим практически, даже если не достигает статистической значимости. Возможно, психолог-практик испробует свою программу на других школьниках или в других условиях или задастся вопросом, чем отличаются эти дети от тех, кому программа не помогла, — в обоих случаях сопоставление статистической и практической значимости полезно для науки.
Значимость, связанную с включением результата в контекст научной жизни, мы бы назвали метааналитической. Напомним пример про телепатию: насколько мы были бы готовы опубликовать статистически значимые результаты в пользу телепатии, если знаем, что 20 предыдущих похожих исследований не дали никаких интересных результатов? Другой пример: изменится ли наша интерпретация некоторого результата, значимость которого относительно нуль-гипотезы 0.08, если мы знаем, что из десяти похожих работ в семи была получена значимость менее 0.05, а в остальных трех — менее 0.10? Еще раз обратим внимание, что в методологии проверки нулевой гипотезы речь идет о единичном исследовании, но результаты нескольких исследований могут быть далее сопоставлены содержательно (теоретически) или при помощи статистики (метаанализ).
>> следующий параграф>>
[1] «Более тяжелые хвосты» — статистический термин, означающий, что вероятности больших отклонений от нуля для распределения Стьюдента больше, чем для стандартного нормального распределения. Подробнее в параграфе 5.2.
[2] Буква Т в названии критерия в литературе встречается как заглавная, так и строчная. Более того, в русской версии SPSS употребляется строчная буква, а в английской — заглавная. Мы всюду, кроме отсылок к пунктам меню русской версии, употребляем заглавную букву в названии Т-критерия и строчную в сочетании «t-статистика».
[3] В литературе слово «квантиль» иногда относят к женскому роду. Нам не удалось найти авторитетных указаний на этот счет.
[4] Пока будем понимать степени свободы чисто рецептурно — разъяснения даны в приложении 4.
[5] В некоторых случаях можно учитывать знак разности и применять односторонние критерии, связанные с односторонними хвостами распределения. Мы обсудим этот вопрос в главе 7.
[6] Правильнее говорить: «принимается альтернативная гипотеза, значимость равна…». Слова «уровень значимости» исходно относились к заранее, еще до проведения эксперимента (или иного измерения) выбранному критерию.
[7] Ситуация в мировой практике начинает меняться.