Умение «читать» данные в табличном и графическом представлении — важное профессиональное качество психолога. В первом параграфе главы, посвященной двухфакторному дисперсионному анализу, мы сосредоточимся на этом аспекте работы с данными, оставив математические подробности второму параграфу.
8.1.1. Двухфакторная схема эксперимента. Пример сложения воздействий
Мы рассмотрим результаты эксперимента по восприятию кратковременно предъявляемых слов. Испытуемым на экране монитора последовательно предъявлялись слова из одного и того же набора в случайном порядке. Каждое слово появлялось четыре раза в четырех различных вариантах условий, образованных парами значений независимых переменных (факторов).
Фактор 1 — длительность предъявления (два уровня: 100 мс и 200 мс),
Фактор 2 — контрастность изображения (два уровня: низкая и высокая).
Зависимая переменная — процент правильно опознанных слов.
Средние значения по всему набору слов задаются таблицей
Таблица 8.1.1(1)
Пример сложения воздействий в двухфакторном дизайне
| Процент правильных ответов | ||
| Длительность 100 мс | Длительность 200 мс | |
| Низкая контрастность | 10 | 15 |
| Высокая контрастность | 20 | 25 |
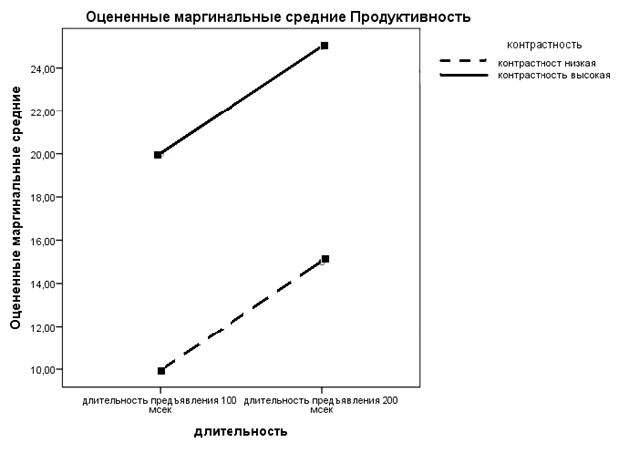
Рис. 8.1.1(2). Групповые средние для двух уровней двух факторов для примера подпараграфа 8.1.1.
В данном случае факторы действуют независимо друг от друга. При любом значении длительности предъявления увеличение контрастности прибавляет 10% правильных ответов. Также и независимо от контрастности увеличение длительности предъявления прибавляет 5% правильных ответов. На практике такая точность сложения воздействий, разумеется, не встречается.
Статистический пакет SPSS выводит средние групповые значения в виде графика (рис. 8.1.1(2)). Независимость действия факторов проявляется на графике параллельностью линий — расстояние между линиями одинаково для обоих значений аргумента «длительность».
8.1.2. Двухфакторная схема эксперимента. Пример сильного взаимодействия
Факторы предыдущего примера измерялись явно в шкале порядка или более сильной шкале интервалов: по крайней мере, вполне осмысленно говорить о большей контрастности и большем времени экспозиции. Для дисперсионного анализа достаточно, чтобы фактор измерялся в номинативной шкале, где отношения «больше-меньше» не имеют смысла.
Рассмотрим следующий пример. В учебном заведении, готовящем специалистов для текстильной промышленности, проводилось исследование связи креативности, которая измерялась с помощью теста Гилфорда, с доминантностью мозговых полушарий. Результаты свидетельствовали об отсутствии преимуществ в креативности как у левшей, так и у правшей. Однако при принятии во внимание специализации обследованных студентов картина оказалась и более сложной, и значительно более интересной. В каждой клетке таблицы представлены средние результаты десяти испытуемых.
Таблица 8.1.2(1)
Пример сильного воздействий в двухфакторном дизайне
| Показатель креативности | ||
| Специальность «художник» | Специальность «механик» | |
| Левши | 20 | 10 |
| Правши | 10 | 20 |
Обратим внимание, что средние значения креативности равны 15 баллам как у левшей, так и у правшей; как у механиков, так и у художников (среднее значение, например, креативности у художников — это среднее арифметическое чисел в соответствующем столбце таблицы; аналогично для других средних). Однако мы видим, что художники-левши оказываются более креативными, чем их праворукие коллеги, а у механиков картина как раз обратная: правши более креативны, чем левши.
В подобных случаях говорят о сильном взаимодействии факторов. Факторы доминантности и специализации по отдельности не влияют заметно на средние значения креативности (однофакторный дисперсионный анализ, как и другие статистические критерии, указал бы на полное отсутствие влияния), но оказывается, что при совместном рассмотрении обоих факторов обнаруживаются важные зависимости: более тщательный анализ тестового материала показал, что художники и механики добиваются одинаковых количественных показателей теста креативности разными средствами, что и дает преимущество в одном случае левшам, а в другом — правшам. На графике это сильное взаимодействие факторов при отсутствии воздействия факторов в среднем выглядит так, как показано на рис. 8.1.2(2).
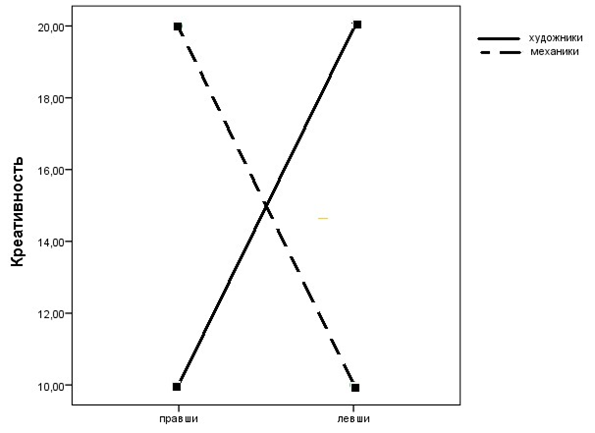Рис. 8.1.2(2). Групповые средние для двух уровней двух факторов для примера в подпараграфе 8.1.2.
8.1.3. Двухфакторная схема эксперимента. Комбинация влияния факторов и взаимодействия. Интерпретация
В исследовательской практике чаще всего приходится встречаться с наложением более или менее сильного прямого влияния факторов и их взаимодействия. В данном примере описано исследование влияние силы мотивации студентов и опыта преподавателей на учебные результаты студентов. В начале семестра оценивалась мотивация студентов. Студенты были в случайном порядке поделены между тремя учебными группами так, чтобы в каждой учебной группе было равное количество студентов с низкой, средней и высокой мотивацией к обучению.
Три преподавателя — начинающий, обладающий средним опытом преподавания и опытный преподаватель — вели занятия каждый в своей группе. В конце семестра оценили знания студентов по предмету по десятибалльной шкале. Средние оценки по группам изображены на графике (рис. 8.1.3(1)).
Как мы говорили, способность «читать» подобные графики составляет важную часть умений психолога — исследователя и практика. Прежде чем перейти к чтению наших интерпретаций, попытайтесь дать интерпретацию самостоятельно.
По графику можно видеть, во-первых, что студенты с более высокой мотивацией в среднем учатся лучше при любом преподавателе. Во-вторых, опытный преподаватель достигает в среднем более высоких результатов при любой мотивации студентов. Эти результаты вполне согласуются с ожиданиями. В-третьих, весьма интересный результат дает взаимодействие факторов: можно видеть, что при низкой мотивации изменение квалификации преподавателя от низкой к средней и от средней к высокой изменяет результат в среднем на один балл (не желающему учиться студенту помочь трудно). То же самое можно сказать и о влиянии квалификации на результат высоко мотивированных студентов (они достигают хороших результатов собственными усилиями). При средней мотивации квалификация преподавателя очень существенна и ее влияние на среднюю оценку студентов более чем в два раза сильнее, чем при низкой и высокой мотивации.
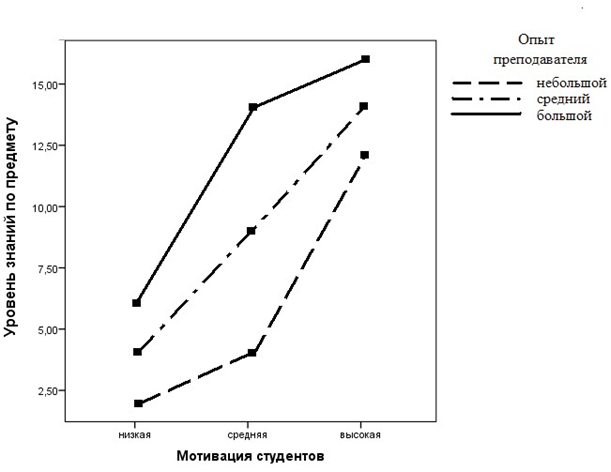Рис. 8.1.3(1). Групповые средние для трех уровней трех факторов.
Определение 8.1.3(2). Если на разных уровнях первого фактора второй фактор оказывает на зависимую переменную различное воздействие, то говорят о влиянии взаимодействия факторов[1].
Не будет преувеличением сказать, что самые интересные результаты в экспериментальных психологических исследованиях, использующих двухфакторный дисперсионный анализ, есть результаты о взаимодействии факторов.
Далее мы разберем несколько примеров. Результаты будут даны в графическом виде, и в данном параграфе их интерпретация будет чисто качественной, без учета значимости. Параллельно эти же примеры будут разобраны в практикуме данной главы. Мы рекомендуем, если это возможно, выполнять задания практикума непосредственно после чтения текстов примеров в данном параграфе.
Отметим для читателей, которым сложность дальнейшего изложения покажется превышающей их силы, что принцип оценивания значимостей не отличается от аналогичного принципа для однофакторного дисперсионного анализа: воздействие факторов, как и их взаимодействие, будет характеризоваться подобранными показателями дисперсии, рост которых с очевидностью свидетельствует в пользу наличия соответствующего влияния фактора или взаимодействия. Эти дисперсии будут делиться на внутригрупповую дисперсию, которая остается постоянной как при наличии влияния, так и при его отсутствии. Результаты оцениваются в сопоставлении с соответствующими квантилями распределения Фишера. На выходе даются оценки значимости влияния отдельно по каждому из двух факторов и взаимодействию между ними.
В книге Е.В. Сидоренко (Сидоренко, 2000) описано исследование уровня доминантности у взрослых мужчин и женщин. Кроме пола, исследователи учитывали порядок рождения испытуемых в семье: старшие дети, средние дети и младшие дети. Авторы предполагали, что доминантность должна быть выше у людей, которые были первенцами в своих семьях, и ниже у средних и тем более младших детей. Однако результат оказался более интересным (рис. 8.1.4(1)). Как и в предыдущем случае, рекомендуем переходить к нашей интерпретации после самостоятельной попытки.
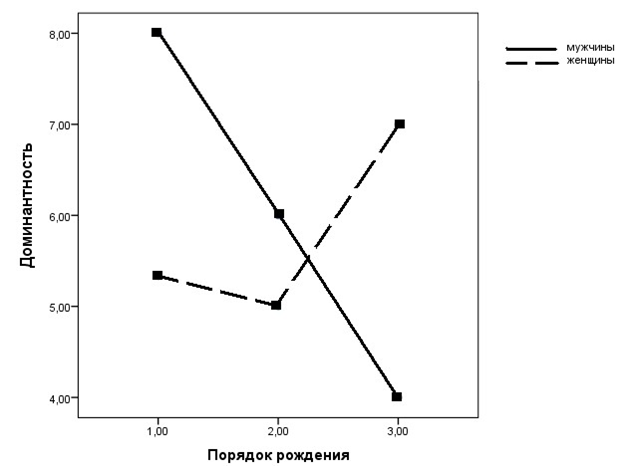Рис. 8.1.4(1). Групповые средние для трех уровней трех факторов.
Гипотеза исследователей оправдалась только наполовину. Доминантность ожидаемо больше у мужчин и падает у более поздних детей — за одним очень интересным исключением. Третья по рождению девочка оказывается более доминантной, уступая только мальчику-первенцу. Интерпретацию этого факта мы оставляем читателю.
8.1.5. Пример. Закон Йеркса-Додсона
Один из самых интересных психологических законов гласит: наилучшее выполнение задания обеспечивается не сильной и не слабой, а некоторой средней мотивацией.
Вот пример, взятый из работы «Экспериментальная психология»[2]. Приведены результаты исследования, проведенного на крысах. Коротко схему исследования можно описать так. Задача животных состояла в различении двух объектов различной яркости, при этом один из ответов оценивался как неправильный. Выделялись три различных уровня сложности различения объектов. Кроме того, предусматривались три уровня мотивации, а именно слабый, средний или сильный электрический удар за ошибки. Общие результаты, полученные в исследованиях, представлены на рис. 8.1.5(1), взятом из упомянутой работы[3].
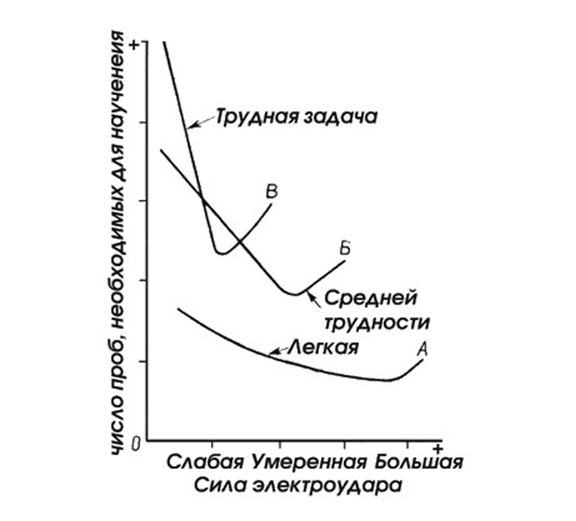Рис. 8.1.5(1). Результат исследования Йеркса-Додсона. По оси абсцисс отложена сила мотивации (сила удара током). По оси ординат — количество проб, понадобившихся для формирования навыка различения
По рисунку видно, что оптимальная мотивация лежит в середине диапазона, причем для сложных задач оптимальна более слабая мотивация, чем для простых.
>> следующий параграф>>
[1] Мы дали не вполне корректную формулировку с целью сделать ее максимально простой и понятной. На самом деле говорить о воздействии или влиянии факторов с полным правом можно только в ситуации причинной связи между независимой и зависимой переменными. Поскольку обоснование причинной связи невозможно сделать чисто статистически, то в общем случае в последнее время специалисты по математической психологии предлагают использовать более аккуратные слова, которые не вводят в заблуждение: «эффект» и «вклад» вместо «влияние» и «воздействие».
[2] Фресс П., Пиаже Ж. (ред.), Экспериментальная психология. — Вып. 5. — М.: Прогресс, 1975/ — C. 119-125
[3] В задании практикума 8.3(6). будут представлены модельные данные и построен график в формате SPSS.