4.1.1. Стандартное нормальное распределение
Среди распределений случайных величин особо выделяется так называемое нормальное распределение. Его статус связан с тем, что нормальное распределение является предельным случаем распределения самых разнообразных массовых процессов. Например, если 1000 раз подкинуть монету, то вероятности того, что количество выпавших гербов попадет в определенный интервал, можно вычислить с хорошей точностью, предполагая, что результат имеет нормальное распределение.
Не только подобные экспериментальные, но и разнообразные практические ситуации дают похожие на нормальное распределения. Например, если станок штампует семидесятимиллиметровые гвозди, то их реальная длина будет колебаться вокруг семидесяти миллиметров приблизительно по закону нормального распределения. Очень часто приблизительно нормально распределены количественно измеряемые признаки в биологических видах — например, таковое распределение будет иметь размер листа на растущей во дворе березе.
Все эти совпадения не случайны. Одна из важнейших теорем теории вероятностей утверждает, что сумма большого числа независимых случайных величин при достаточно большом количестве слагаемых и не слишком сильно отличающихся дисперсиях имеет приблизительно нормальное распределение. Эта теорема объясняет нормальность распределения разнообразных количественных признаков в природе и технике: если признак зависит от большого количества независимых факторов, то о нем можно говорить как о результате суммирования случайных вариаций каждого из этих факторов, что и приводит к нормальному распределению. В частности, многие переменные в психологии также можно считать суммой независимых вкладов различных факторов.
Мы начнем с так называемого стандартного нормального распределения. Его плотность выражается формулой
\[ f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \].
График этой функции изображен на рис. 4.1.1(1).
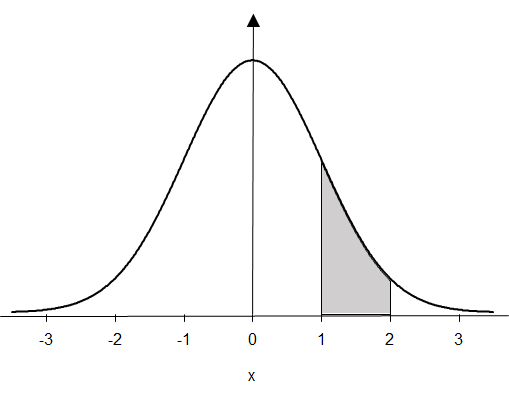Рис.4.1.1(1). График плотности стандартного нормального распределения.
На рисунке выделена область под графиком плотности, ограниченная слева и справа значениями аргумента 1 и 2 соответственно. Площадь этой области и есть вероятность того, что испытание данной случайной величины приведет к появлению числа между единицей и двойкой. Вся площадь под графиком равна, разумеется, единице, поскольку этой площади соответствует вероятность того, что случайная величина примет какое-нибудь значение, т.е. единица.
Несмотря на то что значение\( f(x)\) можно вычислить для любого x, фактически при x < -4 и x > 4 значения функции так малы, что для наших целей ими можно пренебрегать. Это значит, что результат испытания стандартной нормально распределенной случайной величины практически достоверно содержится в интервале от -4 до 4 (вероятность этого равна примерно 0.9998).
Достаточно очевидно, что математическое ожидание стандартной нормально распределенной случайной величины (которую мы далее будем обозначать \( N(0, 1) \)) равно нулю, поскольку график плотности распределения симметричен относительно нуля. Дисперсия стандартной нормальной величины\( N(0, 1) \) также простейшая из возможных — она равна единице.
4.1.2. Нормальное распределение в общем виде
Если подбрасывать монетку 100 раз, то, как мы говорили, количество выпадений гербов будет иметь приблизительно нормальное распределение (это утверждение называется теоремой Муавра-Лапласа). Математическое ожидание биномиальной случайной величины \( B(100, 1/2) \), которая описывает данный процесс, равно 50, дисперсия равна 100-кратно увеличенной дисперсии [1], рассчитанной для одного броска (равной 1/4), т.е. равна 25, а корень из дисперсии (среднеквадратическое отклонение) равен 5. Нормальное распределение с такими параметрами задается формулой
\[ f(x)=\frac{1}{\sqrt{2\pi}\cdot5}e^{-\frac{(x-50)^2}{2\cdot5^2}} \]..
Число 5 здесь — это среднеквадратическое отклонение, а 50 — математическое ожидание. График этой функции симметричен относительно вертикальной прямой \( x=50 \). По сравнению со стандартным, график растянут в 5 раз вдоль оси абсцисс и во столько же раз сжат вдоль оси ординат.
Замечание 4.1.2(1). Формула становится понятней, если среднеквадратическое отклонение обозначить, как мы уже делали, буквой σ, а математическое ожидание буквой a:
\[ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-a)^2}{2\sigma^2}} \].
График этой функции симметричен относительно вертикальной прямой a, растянут по сравнению со стандартным в σ раз[2] и во столько же раз сжат сверху вниз.
Поскольку равномерные сжатие и растяжение сохраняют соотношения площадей частей, то мы получаем простой способ оценки вероятностей для близких к нормальному распределений, который мы можем использовать для решения большого числа разнообразных задач.
Без доказательств, которые желающие могут провести самостоятельно, приведем важные свойства нормально распределенных случайных величин.
Свойство 4.1.2(2). Если \( Y \) нормально распределенная случайная величина, то \( Y+C \) также имеет нормальное распределение (\( C \) — любая положительная или отрицательная константа). Математические ожидания этих величин связывает естественное соотношение
\[ M_{Y+C}=M_Y+C \].
Дисперсии при этом остаются неизменными:
\[ D_{Y+C}=D_Y \].
Свойство 4.1.2(3). Если \( Y \) нормально распределенная случайная величина, C положительная константа, то также имеет нормальное распределение (для отрицательных C это также верно, но нас такие случае не интересуют). Дисперсии этих величин связывает соотношение
\[ D_{{Y}\over{C}}=\frac{D_Y}{C^2} \]
Если математическое ожидание \( Y \) было равно нулю, то \( Y /C\) также будет иметь нулевое математическое ожидание.
На этих свойствах основаны методы приближенного расчета вероятностей путем сведения к стандартной нормальной величине.
4.1.3. Задачи на нормальное приближение распределений
Упражнение 4.1.3(1). Какова вероятность того, что при 100-кратном подбрасывании симметричной монеты количество выпавших гербов превысит 60?
Решение. Обозначим нашу случайную величину через \( Y \). Как уже говорилось, эта случайная величина имеет близкое к нормальному распределение с математическим ожиданием 50, дисперсией, равной 25, и среднеквадратическим отклонением 5. Случайная величина \( Y-50 \) будет иметь приближенно нормальное распределение с нулевым математическим ожиданием, а случайная величина к тому же будет иметь дисперсию, равную единице (при сохранении нулевого математического ожидания), т.е. будет иметь приближенно стандартное нормальное распределение. Количеству гербов больше 60 для исходного условия будет соответствовать событие «испытание стандартной нормально распределенной случайной величины N привело к появлению результата, превышающего \( (60-50)/5=2 \)».
Ниже приведена таблица распределения стандартной нормальной величины. Напротив чисел от 0.1 до трех стоят вероятности того, что эта случайная величина примет значение от нуля до данного числа — значение функции \( \Phi(x) \). Например, вероятность того, что \( N(0, 1) \) примет значение между нулем и единицей равна 0.341.
Таблица 4.1.3(2). Распределение стандартной нормальной случайной величины
| x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0.1 | 0.040 | 1.1 | 0.364 | 2.1 | 0.482 |
| 0.2 | 0.079 | 1.2 | 0.385 | 2.2 | 0.486 |
| 0.3 | 0.118 | 1.3 | 0.403 | 2.3 | 0.489 |
| 0.4 | 0.155 | 1.4 | 0.419 | 2.4 | 0.492 |
| 0.5 | 0.192 | 1.5 | 0.433 | 2.5 | 0.494 |
| 0.6 | 0.226 | 1.6 | 0.445 | 2.6 | 0.495 |
| 0.7 | 0.258 | 1.7 | 0.455 | 2.7 | 0.497 |
| 0.8 | 0.288 | 1.8 | 0.464 | 2.8 | 0.497 |
| 0.9 | 0.316 | 1.9 | 0.471 | 2.9 | 0.498 |
| 1.0 | 0.341 | 2.0 | 0.477 | 3.0 | 0.499 |
В таблице дана вероятность попадания в промежуток (0; 2), она равна 0.477 (для непрерывных распределений включение или не включение границ интервалов, естественно, не меняет вероятностей, поэтому мы не будем уточнять, замкнутый имеется в виду интервал или открытый). Поскольку вероятность попадания \( N(0, 1) \) в интервал от нуля до бесконечности равна 0.5, то вероятность попадания в промежуток от 2 до бесконечности равна \(0.5−0.477=0.023\) (рис. 4.1.3(3)а).
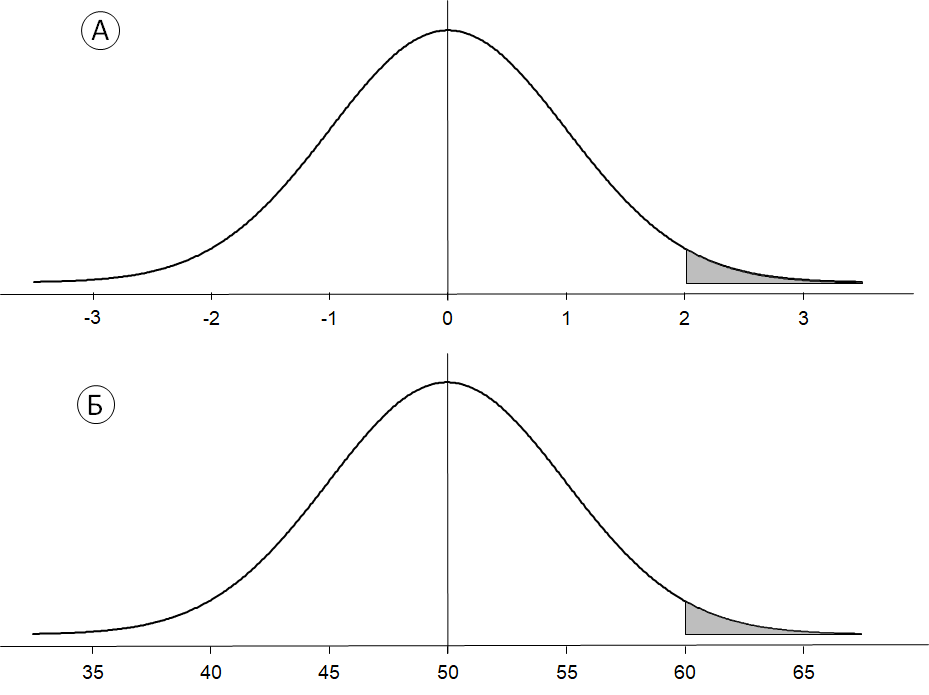Рис. 4.1.3(3) Нормальное приближение частот биномиального распределения.
Пример 4.1.3(4). В исследовании проверяется гипотеза о том, что просмотр телевизионных новостей увеличивает тревожность. У 100 испытуемых измеряется уровень ситуативной тревожности перед и после просмотра новостей. Если в результате получено, что у 60 испытуемых уровень тревожности повысился после просмотра новостей, то вряд ли этот результат можно считать случайным, поскольку тогда результат «60 испытуемых стали более тревожными» соответствует выпадению 60 гербов при 100 бросаниях симметричной монеты. При переходе к нормальному приближению вероятность того, что число гербов будет меньше 60, приравнивается приблизительно к вероятности попадания \( N(0, 1) \) в интервал \( (-\infty;2) \), которая равна 0.023 (рис. 4.1.3(3)б).
Замечание 4.1.3(5) Вероятно, для читателя этот результат довольно неожиданный: обыденная интуиция говорит нам, что 65 из 100 не слишком удивительный результат. В таких случаях теория вероятностей нас уверенно поправляет.
Замечание 4.1.3(6). Когда мы используем нормальное приближение дискретного распределения, для полной точности надо вводить специальную поправку. Ведь для нормального распределения включение или не включение граничного значения интервал не меняет вероятности попадания в интервал, а для дискретного распределения события «больше 65» и «больше либо равно 65» имеют разные вероятности.
Для более точного расчета такого рода вероятностей удобно использовать специальные калькуляторы, которые можно найти в интернете. В качестве примера можно привести калькулятор вероятностей и квантилей нормального распределения, расположенный по адресу https://keisan.casio.com/exec/system/1180573188. В нём необходимо задать три параметра: интересующий нас процентиль (percentile x), математическое ожидание (mean μ) и стандартное отклонение (standard deviation σ) нормальной случайной величины. После этого по нажатию кнопки Execute производится расчёт, в таблице ниже можно найти три результата: probability density f — значение функции плотности случайной величины в точке заданного квантиля; lower cumulative P – вероятность выпадения значения случайной величины ниже указанного квантиля (нижний «хвост», отсекаемый квантилем); upper cumulative Q — вероятность выпадения значения случайной величины выше указанного квантиля (верхний «хвост», отсекаемый квантилем). Также может быть полезна визуализация результата, представленного на графике, который меняется в зависимости от заданных условий. Для расчета вероятности из упражнения 4.1.3(1) следует указать процентиль 60, математическое ожидание 50 и стандартное отклонение 5. Полученный результат будет следующим:
| Normal distribution | value |
| probability density f | 0.010798193 |
| lower cumulative P | 0.977249868 |
| upper cumulative Q | 0.022750132 |
Так как нас интересует вероятность о выпадении больше 60 орлов, то есть верхний хвост распределения, то ответ следует искать в строке upper cumulative Q, значение, содержащееся там совпадает с результатом, полученным с помощью таблиц с точностью до округления. Другим удобным инструментом расчета вероятностей нормального распределения является дополнение distrACTION в Jamovi, о котором мы кратко расскажем в третьей части этой главы.
>> следующий параграф >>
[1] По теоремам 3.2.5(3) и 3.2.5(5) математическое ожидание и дисперсия суммы независимых случайных величин равны сумме математических ожиданий и дисперсий слагаемых.
[2] Если σ<1, то «растяжение в σ раз» означает сжатие. Например, растяжение в 0.5 раза — это сжатие в 2 раза.