В тех главах нашего учебника, где рассматривались различные оценки, вычисляемые с помощью сумм квадратов, возникал вопрос о числе степеней свободы для этих сумм. Первый раз такой вопрос возник, когда в выборочной оценке дисперсии сумма квадратов отклонений делилась не на n (количество слагаемых под знаком корня), а на \( n-1 \). Затем более серьезные вопросы возникали, когда объявлялось, что в одновыборочной t-статистике в знаменателе формулы под корнем стоят n слагаемых, представляющих собой квадраты отклонений, но эта сумма имеет \( n-1 \) степеней свободы. За всеми этими и другими аналогичными случаями, которые встретились нам в курсе статистических методов, стоит одна и та же суть дела, которую мы сейчас и рассмотрим.
Мы разберем простейший пример такого снижения числа степеней свободы и разъясним, как он должен обобщаться. Доказательство основного утверждения будет проведено для случая плоскости, требующего фактически только хорошего уровня школьных знаний, но обобщение доказательства требует понимания «устройства» n-мерного пространства, т.е. подразумевает знакомство с основами линейной алгебры.
Теорема П3(1). Пусть у нас имеется стандартная нормально распределенная случайная величина X и ее n независимых испытаний \( \{X_1, X_2, \dots , X_n\} \). Пусть случайная величина \( \overline{X} \) выражается через эти испытания по формуле \( \overline{X}=\frac{1}{n}(X_1+\dots+X_n) \), а случайная величина \( S^2 \) по формуле
\[ S^2=\frac{1}{n-1}((X_1-\overline{X})^2+\dots+(X_n-\overline{X})^2) \]
Тогда случайная величина \( S^2 \) имеет распределение Хи-квадрат с числом степеней свободы, равным \( n-1 \).
Прежде чем доказывать теорему, надо разъяснить, что представляет собой случайная величина, имеющая распределение Хи-квадрат с k степенями свободы. Напомним, что такое распределение имеет случайная величина
\[ \frac 1k(N_1^2+\dots+N_k^2), \]
где \( N_i \) — независимые испытания стандартной нормальной случайной величины.
Мы рассмотрим сначала распределение Хи-квадрат с двумя степенями свободы, которое оказывается очень похоже на распределение квадрата длины расстояния от центра мишени до пулевого отверстия (см. 3.1.5).
Для понимания дальнейшего материала требуется составить понятие о двумерной стандартной нормальной величине, которая и описывает распределение пулевых отверстий нашего примера.
П3.1. Двумерное стандартное нормальное распределение
Двумерное стандартное нормальное распределение можно задать как распределение положения на плоскости случайной точки, каждая из координат которой независимо описывается стандартным нормальным распределением. Плотность распределения положения точки будет функцией, заданной на плоскости. Вероятность того, что результат испытания двумерной величины попадет в определенную область, вычисляется как интеграл этой функции по данной области. Чтобы понять суть дела, вспомним, что для обычного стандартного нормального распределения вероятность попадания в очень маленький отрезок длины \( l_x \) с левым концом в точке a оси X может быть приблизительно рассчитан как произведение длины отрезка на значение плотности распределения в точке a. Это произведение равно
\[ l_x\cdot \frac1{\sqrt{2\pi}}\cdot e^{-a^2/2} \]
Для нашего двумерного распределения с независимыми координатами вероятность попадания результата в очень маленький прямоугольник с левым нижним концом в точке (a, b) и со сторонами \( l_x \) и \( l_y \), равна произведению вероятности попадания X-ой координаты в отрезок \( l_x \), начинающийся в точке a, и вероятности попадания Y-ой координаты в отрезок длины \( l_y \), начинающийся в точке b. Это произведение записывается формулой
\[ l_x\cdot l_y \cdot \frac1{\sqrt{2\pi}}\cdot e^{-a^2/2}\cdot \frac1{\sqrt{2\pi}}\cdot e^{-b^2/2}, \]
т.е. равно площади прямоугольника (она равна \( l_x\cdot l_y \)), умноженной на произведение покоординатных плотностей, равное
\[ \frac1{\sqrt{2\pi}}\cdot e^{-a^2/2}\cdot \frac1{\sqrt{2\pi}}\cdot e^{-b^2/2}. \]
Если превратить произведение экспонент в экспоненту суммы, то произведение плотностей равно
\[ \frac1{2\pi}\cdot e^{-(a^2+b^2)/2}. \]
Функция
\[ p(x,y)=\frac1{2\pi}\cdot e^\frac{-(x^2+y^2)}{2} \]
и задает плотность двумерного стандартного нормального распределения.
П3.2. Свойства двумерного стандартного распределения
Свойство П3.2(1). Проекция случайной точки, положение которой задается двумерной стандартной случайной величиной, на любую прямую, проходящую через начало координат, имеет стандартное нормальное распределение.
Нам потребуется частный случай этого свойства, когда прямая наклонена под углом 45 градусов к осям.
Сделаем двумерную замену переменных, определяемую уравнениями
\[ x’=\frac{x+y}{\sqrt{2}}, y’=\frac{y-x}{\sqrt{2}}. \]
Новые координатные оси являются биссектрисами старых координатных углов. Старые координаты выражаются тогда через новые по формулам
\[ x=\frac{x’-y’}{\sqrt{2}}, y=\frac{x’+y’}{\sqrt{2}}. \]
Подставим эти выражения в формулу плотности распределения и получим для новых координат
\[ p(x’,y’)=\frac1{2\pi}\cdot e^{-((\frac{x’-y’}{\sqrt{2}})^2+(\frac{x’+y’}{\sqrt{2}})^2)/2}. \]
Преобразуем выражение
\[ \left(\frac{x’-y’}{\sqrt{2}}\right)^2+\left(\frac{x’+y’}{\sqrt{2}}\right)^2, \]
возведя в квадрат дроби и приведя подобные члены:
\[ \left(\frac{x’-y’}{\sqrt{2}}\right)^2+\left(\frac{x’+y’}{\sqrt{2}}\right)^2=\frac{(x’)^2-2x’y’+(y’)^2+(x’)^2+2x’y’+(y’)^2}2= (x’)^2+(y’)^2. \]
Это значит, что плотность двумерного нормального распределения в новых осях выглядит точно так же, как и в старых:
\[ p(x’,y’)=\frac1{2\pi}\cdot e^{-((x’)^2+(y’)^2)/2}. \]
В этом нет ничего удивительного — поскольку \( x^2+y^2=C \) есть уравнение окружности, то наша плотность \( p(x,y) \) имеет одинаковые значения на всякой окружности с центром в начале координат, т.е. обладает центральной симметрией, поэтому и выглядит одинаково при любых поворотах системы координат.
Свойство П3.1(1), стало быть, выражает тот факт, что, задав двумерное нормальное распределение какими-то осями, мы затем можем смотреть на это распределение, так сказать, наклонив голову (для нашего преобразования координат достаточно наклонить голову влево на 45 градусов, чтобы новые оси выглядели точно как старые при вертикальном положении головы) и получая новые стандартно нормально распределенные проекции на новые оси.
П3.3. Свойства случайной величины, являющейся квадратом модуля двумерной стандартной нормальной случайной величины
Квадратом модуля мы здесь для краткости называли квадрат расстояния от точки на плоскости до начала координат. Обозначим двумерную стандартную нормальную случайную величину \( N^2_{sq} \). Обозначим случайные величины — одномерные компоненты, из которых она составлена, и . Изобразим возможный результат ее испытания точкой с координатами (Рис. П3.3(1)). По теореме Пифагора квадрат расстояния равен сумме квадратов координат этой точки, которые могут быть получены возведением в квадрат «осевых» одномерных стандартных случайных величин. Обозначим эти квадраты \( X_1’\) и \(X_2′ \).
По теореме Пифагора
\[ N^2_{sq}=(X_1)^2+(X_2)^2. \]
Но точно так же \( N^2_{sq} \) можно разложить в сумму квадратов и по новым осям \( x’ \) и \( y’ \). Тогда мы получим другое справедливое равенство
\[ N^2_{sq}=(X_1′)^2+(X_2′)^2. \]
Посмотрим теперь, что представляет собой \( N^2_{y’} \). Это проекция двумерной стандартной нормальной случайной величины на ось координат, т.е. (одномерная) стандартная нормальная случайная величина. Для нашей точки \( (X_1,X_2) \) проекция на ось \( X_2′ \) есть точка \( (X_1-\overline{X},X_2-\overline{X}) \). Квадрат длины проекции соответствующего вектора мы можем вычислить по теореме Пифагора через ее координаты: он равен \( (X_1-\overline{X})^2 + (X_2-\overline{X})^2 \).
Таким образом, квадрат одномерной стандартной нормальной случайной величины \( X_2′ \) можно вычислять по формуле \( (X_2′)^2=(X_1-\overline{X})^2 + (X_2-\overline{X})^2 \) через исходные случайные величины \( X_1 \) и \( X_2 \), и этот квадрат случайной величины имеет распределение Хи-квадрат с одной степенью свободы. Но в правой части стоит «заготовка» формулы для оценки дисперсии по двум наблюдениям. Вернемся к оценке дисперсии.
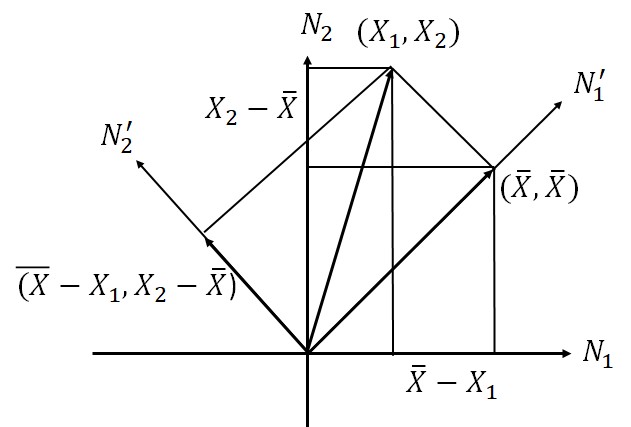
Рис. П3.3(1). Разложение сумм квадратов
Предположим сначала, что математическое ожидание нормально распределенной случайной величины нам известно, а дисперсия неизвестна. Пусть дана случайная величина X с математическим ожиданием \( M_X \). Мы хотим оценить ее дисперсию по выборке. Тогда нам подойдет естественная оценка дисперсии со знаменателем n:
\[ S^2=\frac{1}{n}((x_1-M_X)^2+\dots+(x_n-M_X)^2) \]
Для дискретной случайной величины доказательство того, что это — оценка дисперсии можно провести совершенно аналогично доказательству того, что среднее выборочное есть оценка математического ожидания — надо увидеть, что частоты каждого значения (в данном случае квадрата отклонения) сходятся к соответствующим вероятностям. Для непрерывной случайной величины доказательство технически усложняется, но по смыслу остается тем же.
Если же мы не знаем математическое ожидание и вынуждены использовать его оценку \( \overline{x} \), то надо иметь в виду следующее: \( \overline{x} \) не попадает точно в центр распределения, а смещается в сторону случайного сдвига выборки, грубо говоря, вправо или влево в сторону большего числа членов выборки, случайно там оказавшихся. Это значит, что в среднем разность \( (x-\overline{x})^2 \) оказывается меньше, чем в среднем \( (x_i-M_X)^2 \) Замечательный факт, который мы доказали в частном случае, состоит в том, что этот сдвиг в точности соответствует уменьшению числа степеней свободы на единицу. Например, в разобранном частном случае распределение \( (x_i-M_X)^2 \) в точности совпадает с распределением суммы \( (X_1-\overline{X})+(X_2-\overline{X}) \).
Сумма \( X_1^2+X_2^2 \) разлагается в сумму \( \overline{X}_1^2+\overline{X}_2^2+(X_1-\overline{X})+(X_2-\overline{X}) \).
П3.5. Разложение сумм квадратов в случае больших размерностей
Если теперь рассмотреть выборку объема n испытаний стандартной нормальной случайной величины, то надо разложить квадрат вектора, имеющего стандартное нормальное n-мерное распределение, в сумму квадрата одномерного распределения вдоль вектора (1,1,…,1) (это будет вектор \( (\overline{X}, \overline{X},\dots,\overline{X}) \), квадрат его длины есть \( n\cdot\overline{X} \) — сравни с первой таблицей межгрупповых сумм в дисперсионном анализе); и квадрата \( (n-1) \)-мерного «остатка», который станет ни чем иным, как случайной величиной Хи-квадрат с \( (n-1) \) степенью свободы, если ее разделить на это число \( (n-1) \). Число степеней свободы и есть размерность этого дополняющего подпространства.
П3.6. Оценка дисперсии. Последнее замечание
Если теперь мы захотим оценить неизвестную дисперсию нормально распределенной случайной величины с неизвестным математическим ожиданием, то мы должны воспользоваться формулой
\[ s^2=\frac{1}{n-1}((x_1-\overline{x})^2+(x_2-\overline{x})^2+\dots+(x_n-\overline{x})^2) \]
Если эта дисперсия равна какому-то числу D, то этому же числу будет равно в среднем наше \( s^2 \), имеющее в этом случае распределение, пропорциональное Хи-квадрат с коэффициентом пропорциональности D.
П3.7. Другие разложения сумм квадратов
Каждое отдельное приложение представленного подхода требует особых разложений сумм квадратов и особых доказательств.
Во всех случаях подобных разложений сначала выделяют взаимно ортогональные подпространства в пространстве, размерность которого равна общему числу испытуемых, а затем производят разложение квадрата стандартного нормально распределенного многомерного вектора по этим направлениям (хотя доказательство ортогональности иногда представляет значительную трудность).
Например, разложение сумм квадратов в однофакторном дисперсионном анализе выделяет (1) одномерное подпространство, порождаемое вектором (1, 1,…, 1), (2) \( k-1 \)-мерное подпространство (где k число групп), порождаемое возможными групповыми средними[1]; (3) все остальное «остается» остатку или ошибке, и размерность соответствующего подпространства равна \( n-k \). Если вся выборка взята из одной и той же генеральной совокупности, то пространство «за вычетом» одномерного подпространства средних будет иметь размерность \( n-1 \), а соответствующая оставшейся сумме квадратов случайная величина имеет распределение Хи-квадрат с \( n-1 \) степенями свободы. Выделенные ортогональные подпространства групповых средних и остатка определяют соответствующие распределения Хи-квадрат, частное которых и дает отношение Фишера.
[1] Это сумма одномерных подпространств, заданных средними по каждой группе с условием после выделения общего среднего, что сумма этих средних равна нулю — что и делает размерность подпространства равной \( k-1 \).