3.1.1. Случайная величина. Распределение
Определение 3.1.1(1). Если каждому возможному в результате некоторого испытания случайному событию определенным образом поставлено в соответствие некоторое число, говорят, что этим самым задана случайная величина. Иными словами, случайная величина — это величина, принимающая в результате испытания то или иное случайное числовое значение.
Мы будем обозначать случайные величины большими латинскими буквами \( X \), \( Y \) и т.д.
С каждой случайной величиной связано некоторое множество чисел — значений, которые она может принимать. Закон распределения случайной величины — это множество ее возможных значений вместе с соответствующими вероятностями их появления.
Примеры, которые рассматривались в предыдущей главе, могут интрепретироваться как случайные величины. Таковы: количество выпавших гербов при бросании определенного количества монет, суммы очков на верхних гранях брошенных одной или нескольких игральных костей, уровень тревожности случайно выбранного человека, измеренный с помощью определенной методики.
Далеко не всегда само случайное событие естественно и очевидно характеризуется возможными числовыми значениями. Гораздо чаще для наших целей приходится придумывать специальные полезные числовые характеристики случайных событий.
Пример 3.1.1(2). Разрабатывается методика по развитию функций зрительно-пространственной памяти у детей с отставанием в развитии. Для проверки эффективности методики предполагается давать детям тестовое задание «Рисунок дома», входящее в одну из батарей нейропсихологического обследования, перед началом использования развивающей методики и через несколько недель — после завершения работы с детьми. Полученные рисунки предполагается предъявить эксперту, не указывая, какой из рисунков нарисован испытуемым раньше. Эксперт выберет лучший из двух рисунков, а лаборант напишет в протоколе единицу, если лучшим окажется более поздний рисунок, и нуль в противном случае.
Если методика абсолютно неэффективна, то два рисунка ребенка могут с равными вероятностями продемонстрировать сдвиг к лучшему или к худшему — в силу случайных обстоятельств, например, лучшего или худшего самочувствия ребенка в момент тестирования. Таким образом, в этом случае количество единиц в итоговом протоколе будет случайной величиной. Она будет иметь разобранное в подпараграфе 2.2.4 биномиальное распределение с количеством испытаний n, равным числу тестируемых детей, и равными 0.5 вероятностями того, что второй рисунок окажется лучше или хуже первого. Это распределение совпадает с распределением числа выпавших гербов при n-кратном подбрасывании симметричной монеты. Если методика эффективна, то мы будем иметь случайную величину с иным распределением, в котором единиц будет ожидаемо больше половины, хотя совсем не обязательно, что их будет n.
Перейдем теперь к рассмотрению того, каким образом может быть задан закон распределения случайной величины. Наиболее просто задается распределение в случае, когда случайная величина принимает лишь конечное число значений. В этом случае ее распределение удобно задать таблицей.
Пример 3.1.1(3). Для игральной кости вероятности принять любое из шести значений pавны между собой. Таблица распределения соответствующей случайной величины (обозначим ее через \( X \)) выглядит так
| \( X \) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
В верхней строке записаны возможные значения случайной величины, в нижней, под каждым значением, соответствующая этому значению вероятность.
Пример 3.1.1(4). Подбрасывая три монеты, будем фиксировать количество выпавших гербов. Расчет вероятностей (см. 2.2.4) дает для нашей случайной величины \( Y \) следующую таблицу распределения вероятностей:
| \( Y \) | 0 | 1 | 2 | 3 |
| 1/8 | 3/8 | 3/8 | 1/8 |
Отметим важное обстоятельство. Задание распределения случайной величины подобной таблицей подразумевает, что в результате испытания появится одно и только одно из значений, помещенных в верхнюю строку таблицы. Это значит, что сумма вероятностей, составляющих нижнюю строку, равна единице.
Случайная величина как теоретическая идеализация однозначно определяется своим законом распределения. При этом реализовать ее можно различными способами, как мы уже неоднократно говорили. Все выводы, которые можно сделать об абстрактной, заданной таблицей распределения случайной величине, будут верны и для любой реализации. Именно поэтому имеет смысл развивать общую теорию случайных величин. Вследствие этого мы и будем часто отождествлять случайную величину с ее законом распределения.
Случайную величину, описанную в последнем примере, можно задать и диаграммой распределения (Рис. 3.1.1(5)).
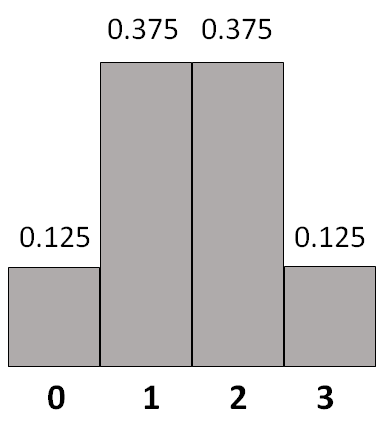Рис. 3.1.1 (5). Диаграмма распределения результатов испытания неизвестного процесса.
3.1.2. Математическое ожидание и выборочное среднее
Предположим, что некий игровой клуб предлагает своим посетителям, заплатив за вход 2000 рублей, 1000 раз сыграть в игру с автоматом, который с указанными в Примере 3.1.1(4) вероятностями выдает за одну игру 0, 1, 2 или 3 рубля. Стоит ли соглашаться на такие условия?
За 1000 игр мы можем ожидать появление примерно 125 нулей (1/8 от 1000), по 375 единиц и двоек (по 3/8 от 1000) и 125 троек. Это значит, что мы выиграем примерно \( 125⋅0+375⋅1+375⋅2+125⋅3=1500 \) рублей, в среднем 1.5 рубля за игру. Мы видим, что соглашаться играть не стоит. Равные шансы выиграть и проиграть будут у нас, если за вход мы заплатим 1500 рублей.
Мы получили средство решать большое количество похожих проблем, причем не только связанных с азартными играми[1]. Эти средства окажутся важной составляющей математических методов в психологических исследованиях. Ответ «полтора рубля за игру в среднем», как легко видеть, получается перемножением значений и их вероятностей: \( 0.125⋅0+0.375⋅1+0.375⋅2+0.125⋅3=1.5 \). По сути, выше мы и сделали это вычисление, только в два этапа: сначала по вероятностям определили ожидаемые количества результатов каждого вида, а потом, поделив на общее количество испытаний, получили произведения значений на ожидаемые частоты, которые и суть вероятности.
Определение 3.1.2(1). Математическим ожиданием случайной величины называется сумма произведений возможных значений этой величины на соответствующие этим значениям вероятности.
Если задать случайную величину \( X \) общей таблицей
| \( X \) | x1 | … | xn |
| p1 | … | pn |
то математическое ожидание X (которое обозначается символом \( M_X \)) задается формулой:
\[ M_X=x_1 p_1+…+x_n p_n \].
Математическое ожидание дает среднее ожидаемое значение результата испытаний, как мы видели в предыдущем примере.
В предыдущей главе мы определили случайную выборку из генеральной совокупности. Поскольку случайные величины не обязательно связаны с выбором из генеральной совокупности, то определение выборки надо расширить.
Определение 3.1.2(2). Выборка значений случайной величины, имеющая объем n, это результат n последовательных независимых испытаний случайной величины.
Определение 3.1.2(3). Средним выборочным значением (коротко — выборочным средним) называется среднее арифметическое значений, составляющих выборку.
Если выборка представляет собой реализацию испытаний случайной величины с известным распределением, то выборочное среднее будет лежать вблизи теоретического среднего — математического ожидания. Говорят, что выборочное среднее оценивает математическое ожидание соответствующей случайной величины.
Поскольку частоты появления исходов испытаний приближаются по мере увеличения объема выборки к вероятностям, постольку и выборочное среднее приближается к математическому ожиданию.
Хотя случайность дает свои коррективы и количества результатов каждого вида будут несколько отличаться от ожидаемых, все же с помощью теории вероятностей можно рассчитать, что практически всегда выборочное среднее по 1000 испытаний для описанной выше игры с автоматом будет лежать в интервале от 1.42 до 1.58 (вероятность такого события равна 0.998, см. параграф 4.2).
Выборка объема n испытаний некоторой случайной величины X обозначается \( \{x_1,x_2,…x_n\} \), а выборочное среднее:
\[ \overline{x}=\frac{1}{n}(x_1+x_2+…+x_n) \]
Следующие важные характеристики случайной величины оценивают разброс колебаний ее значений. Рассмотрим две выборки: {90, 100, 110} и {0, 100, 200}. Как легко видеть, они имеют одно и то же среднее значение — 100. Однако колебания значений первой составляют 20 единиц, а второй — 200 единиц. Наиболее удобной характеристикой разброса оказалась дисперсия.
Определение 3.1.3(1). Выборочная дисперсия, которая обозначается \( s^2 \) рассчитывается для выборки \( \{x_1,x_2,…x_n\} \) по формуле
\[ s^2=\frac{1}{n-1}((x_1-x ̄)^2+(x_2-x ̄)^2+…+(x_n-x ̄)^2) \]
Так же, как и в случае пары «выборочное среднее — математическое ожидание», значение выборочной дисперсии при испытаниях нашей случайной величины располагается вблизи теоретической дисперсии распределения, формулу для расчета которой мы приведем в параграфе 3.2.
3.1.4. Случайная величина и генеральная совокупность
Если интересующий нас параметр в генеральной совокупности принимает какой-то набор значений с соответствующими частотами, то случайный выбор одного представителя из данной совокупности и измерение данного параметра будут тождественны испытанию случайной величины, имеющей то же самое распределение. Рис. 3.1.4(1) одинаковыми графиками отображает распределение параметра (в нашем гипотетическом случае — тревожности) в генеральной совокупности и распределение случайной величины, которая реализуется измерением того же параметра у случайно выбранного представителя генеральной совокупности.
Рис. 3.1.4(1). а) Гистограмма распределения результатов тестирования тревожности у всех граждан РФ (в процентах), б) Диаграмма распределения случайной величины «значение по тесту тревожности случайно выбранного гражданина РФ».
Однако, как мы видим, случайная величина может и не порождаться никакой генеральной совокупностью. Самый простой пример мы рассматривали выше — количество выпадений гербов при подбрасывании монеты. Другой, очень важный пример — выборочное среднее. Даже если мы набираем случайную выборку из генеральной совокупности, распределение возможных значений выборочного среднего не соответствует распределению признака в какой-то простой генеральной совокупности[2].
3.1.5. Непрерывные случайные величины. Распределения и их характеристики
Мы измеряем величины всегда с некоторой точностью. Если длина измеряется рулеткой, на ленте которой нанесены сантиметры, то результатом будет натуральное число, выражающее длину измеряемого предмета в сантиметрах. Более точная рулетка с миллиметровыми делениями даст результаты более точные, но выражающиеся целым числом миллиметров. Если предмет исследования — рост человека, то вариации в генеральной совокупности этого параметра (размах — разность максимального и минимального значения) составят около двух метров. Это значит, что случайная величина «рост в миллиметрах случайно выбранного человека» может принимать любое из примерно 2000 значений. Хотя определения, которые мы ввели выше, позволяют в принципе работать с таким количеством значений, все же это явно неудобно. Если принять во внимание, что точность измерения может увеличиваться неограниченно и при каждом таком увеличении количество значений интересующей нас случайной величины также будет расти, то имеет смысл рассмотреть разумную альтернативу.
Вместо большого количества значений можно рассмотреть сразу бесконечное количество. Эта идеализация вполне наглядна. Предположим, мы, вооружившись ружьем, целимся и стреляем в центр мишени. Нас интересует расстояние от центра мишени до отверстия от пули. Эта случайная величина может меняться от нуля до нескольких метров, а проще всего «с запасом» считать в каких-то случаях возможным, хотя и очень маловероятным, отклонение на любое, как угодно большое расстояние. Мы абстрагируемся от того, что в каждой наличной ситуации обладаем при измерении минимальной единицей, а считаем, что реальное отклонение может быть любым положительным действительным числом, хотя мы и не можем его измерить с точностью, превышающей наши текущие возможности.
Какова в этой идеализации вероятность того, что пуля попадет точно в центр мишени, т.е. случайная величина примет значение в точности 0 при любой точности измерения? Похожий вопрос: какова вероятность того, что пуля отклонится ровно на 1 см? на 3/4 см? на \( \sqrt{2} \) см? На произвольное фиксированное число сантиметров? Такая вероятность не может измеряться положительным числом, поскольку возможных значений слишком (бесконечно) много, поэтому и сумма даже очень маленьких вероятностей в бесконечном числе окажется (бесконечно) больше единицы[3].
Таким образом, вероятность появления каждого значения должна быть равной нулю. Однако нуль нулю рознь. Попасть с пяти метров близко к центру мишени все же вероятнее, чем на миллион километров в сторону или выше. В последнем случае ствол пришлось бы поднять почти вертикально, а такую ошибку не допустит даже очень плохой стрелок.
Для того чтобы различать «большие» нули от «маленьких» вводится функция: так называемая плотность распределения. Рис. 3.1.5(1) показывает плотность распределения для нашего примера. На вопрос «Какова вероятность отклонения пули от центра ровно на 1 см?» плотность распределения дает тривиальный ответ — нуль. Но зато на вопросы типа «Какова вероятность того, что отклонения пули от центра будут лежать между 1 см и 2 см?» ответ будет вполне разумным: эта вероятность измеряется площадью криволинейной трапеции, которая на рисунке заштрихована. Похожим образом вычисляются вероятности отклонения пули от центра в любой интервал между двумя числами[4]. Вся площадь под графиком функции, естественно, должна быть равна единице, поскольку какое-то значение отклонения от центра обязательно будет иметь место, а значит, с вероятностью единица случайная величина примет какое-то неотрицательное значение.
Рис. 3.1.5(1). Плотность распределения случайной величины «Расстояние от точки попадания пули в мишень до центра мишени (в сантиметрах)” . Заштрихована площадь, соответствующая расстоянию от 1 до 2 сантиметров.
Для выборки объема n испытаний непрерывной случайной величины формулы расчета выборочного среднего и выборочной дисперсии те же самые, что и в дискретном случае:
\[ \overline x=\frac{1}{n} (x_1+x_2+…+x_n ), s^2=\frac{1}{n-1}((x_1-x ̄)^2+(x_2-x ̄)^2+…+(x_n-x ̄)^2) \],
хотя формулы расчета теоретических величин — математического ожидания и дисперсии — задаются не суммами, а интегралами. Мы не будем их здесь приводить. Интересующиеся могут обратиться к учебным пособиям по теории вероятностей. Как и в случае дискретных величин, и для непрерывных случайных величин при увеличении объема выборки выборочные среднее и дисперсия стремятся к теоретическим значениям математического ожидания и дисперсии.
3.1.6. Зачем нужны математическое ожидание и дисперсия
Квадратный корень из дисперсии играет важную роль во многих случаях, поэтому введены специальные термины: корень из теоретической дисперсии называется среднеквадратическим отклонением и обычно обозначается строчной греческой буквой \( \sigma\) (читается «сигма»), корень из выборочной дисперсии называется стандартным отклонением и обычно обозначается латинской строчной буквой s. Стандартное отклонение оценивает среднеквадратическое отклонение с тем большей точностью, чем больше выборка. Когда последнее неизвестно, используется эта оценка. Для любой случайной величины с помощью математического ожидания и среднеквадратического отклонения можно рассчитать область наиболее вероятных значений. Если на числовой прямой отложить от математического ожидания вправо и влево отрезки длиной по 3σ, то с вероятностью не меньше чем 8/9 случайная величина будет принимать значения из этой области. Если обозначить математическое ожидание случайной величины \( X \)через \( M_X \), то сказанное выше можно переформулировать так: с вероятностью не меньше 8/9 (т.е. в среднем не реже чем в восьми случаях из девяти) случайная величина \( X \)будет принимать значения из интервала \( [M_X-3σ,M_X+3σ] \) (где \( M_X \) и \( \sigma \) — математическое ожидание и среднеквадратическое отклонение этой случайной величины). Эта оценка верна для любой случайной величины[5], но для тех, с которыми мы обычно имеем дело, вероятность получить значение внутри этого интервала еще значительно ближе к единице.
3.1.7. Простейшие операции над случайными величинами и выборками. Стандартизация
Если на каждой грани игральной кости вырезать еще по одной точке, т.е. увеличить каждое выпадающее значение на единицу, то в терминах случайных величин это будет означать прибавление к случайной величине единицы. Аналогично операция прибавления/вычитания постоянного числа может быть проведена для любой случайной величины: все значения надо изменить на данное число, а вероятности оставить прежними. Математическое ожидание новой случайной величины будет равно прежнему плюс/минус добавляемое число:
\[ M_{(X\pm a)}=M_X\pm a \]
Если к каждому члену выборки \( \{x_1,x_2,…,x_n\} \) составленной из испытаний случайной величины \( X \), прибавить число \( a \), то новое среднее значение будет равно \( \overline{x}+a \). Эту выборку можно считать испытаниями случайной величины \( X +a\), и выборочное среднее будет близко к математическому ожиданию новой величины в том же смысле, в каком близки среднее и математическое ожидание \( M_X \).
При изменении случайной величины на константу ее дисперсия не меняется.
Чтобы умножить/поделить случайную величину на константу, надо умножить/поделить на эту константу каждое её значение, а вероятности оставить прежними. Для игральной кости операция выглядит похоже на операцию прибавления, но вместо вырезания новых точек удобнее будет выгравировать на гранях новые числа, равные соответствующим произведениям.
При умножении случайной величины на константу ее дисперсия умножается на квадрат этой константы. При делении случайной величины на константу ее дисперсия делится на квадрат этой константы.
Есть более полезные примеры этой операции. Вместо количества выпавших гербов при 15-кратном бросании симметричной монеты можно рассчитывать частоты выпадения гербов, деля количество гербов на 15. Математическое ожидание также поделится на 15 и станет равным 0.5, как и в случае одной монеты. В этом нет ничего удивительного: средняя частота выпадения герба в пятнадцати бросаниях и должна колебаться вокруг 0.5.
Если вычесть из случайной величины ее математическое ожидание, то математическое ожидание результата станет равным нулю. Аналогично, если вместо выборки \( \{x_1,x_2,…,x_n\} \) рассмотреть выборку \( \{(x_1-x ̄),(x_2-x ̄),…,(x_n-x ̄)\} \), т.е. вычесть из каждого члена среднее выборочное, то среднее новой выборки будет равно нулю. Такая выборка называется центрированной, а операция вычитания среднего центрированием.
Если поделить случайную величину на среднеквадратическое отклонение, то у новой случайной величины дисперсия будет равна единице (математическое ожидание также поделится на среднеквадратическое отклонение). Аналогично, если вместо выборки \( \{x_1,x_2,…,x_n\} \) рассмотреть выборку \( \{x_1/s,x_2/s,…,x_n/s\} \), т.е. поделить каждый член выборки на стандартное отклонение, то выборочная дисперсия новой выборки станет равной единице, а среднее значение поделится на s.
Объединяя эти две операции, можно получить стандартизованную случайную величину: сначала вычесть математическое ожидание, затем поделить на среднеквадратическое отклонение. Полученная случайная величина будет иметь математическое ожидание равное нулю и дисперсию равную единице. Аналогично можно получить стандартизованную выборку: сначала из всех членов выборки вычесть среднее значение, затем поделить на стандартное отклонение. Полученная выборка
\[ \{\frac{x_1-\overline{x}}{s},\frac{x_2-\overline{x}}{s},\dots,\frac{x_n-\overline{x}}{s}\} \]
будет иметь среднее значение равное нулю и выборочную дисперсию равную единице. Все доказательства приведены в параграфе 3.2.
Стандартизация важна как составная часть разнообразных операций. Поясним ее смысл. В параграфе, посвященном измерению, сообщалось, что для интервальных шкал допустимо линейное преобразование \( x’=ax+b \). Поскольку ни нуль шкалы, ни единица измерения не имеют чаще всего определенного смысла, то предпочтительной единицей оказывается стандартное отклонение генеральной совокупности (или ее выборочная оценка). В самом деле, что значит оценка двенадцать баллов по шкале тревожности некоторого нового теста? Если же окажется, что среднее значение тестовых баллов, оцененное по достаточно большой выборке, т.е. с достаточной точностью, равно шести, а стандартное отклонение равно четырем, то респондент, получивший двенадцать сырых баллов, имеет стандартизованную оценку \( (12-6)/4=1.5 \), а это означает, что он входит в 10 процентов наиболее тревожных людей в генеральной совокупности. Вывод опирается на тот почти повсеместный факт, что тестовые оценки распределены в генеральной совокупности по закону, близкому к нормальному (см. следующую главу), а для него вероятности, относимые к стандартизованным баллам, постоянны и записаны в хорошо известных таблицах. Стандартизованные баллы называются также Z-баллами или Z-оценками (по-английски Z-scores). Ими измеряют не только оценки конкретных лиц, но и разности средних оценок по группам и многое другое.
>> следующий параграф>>
[1] Заметим, что первоначально теория вероятностей развивалась прежде всего на примерах задач о разумных ставках в аналогичных играх.
[2] В этом случае генеральная совокупность все же может быть определена, но как весьма абстрактный математический объект.
[3] Ситуация на самом деле несколько сложнее. Для обоснования утверждения надо сослаться на то, что точки на плоскости в каком-то смысле равноправны: например, вероятности попадания в точки окружности, равноотстоящие от центра прицеливания, равны. Тогда окажется бесконечно много точек с некоторой определенной вероятностью, и сумма будет заведомо бесконечной.
[4] В области отрицательных значений аргумента (левее начала координат) случайная величина значений принимать не может, поскольку отрицательных расстояний не бывает. Плотность распределения в этой области равна нулю. В отличие от положительных значений аргумента, вероятность также равна нулю и для попадания отклонения пули в интервал между любыми отрицательными числами.
[5] Она следует из неравенства Чебышева. Доказательство можно найти в (Кричевец, Шикин, Дьячков, 2003).