4.3. Нормальное распределение. Практикум

Пример 4.3(1). Рассмотрим пример нормального распределения в психологическом исследовании. Допустим, мы измерили коэффициент интеллекта (по стандартной шкале IQ) у нормальных взрослых испытуемых. Модельные данные такого исследования представлены в файле NormIQ.sav. В единственной переменной IQ содержатся баллы IQ 150 испытуемых. Известно, что шкала IQ строилась так, что средний балл этого показателя равен 100, а стандартное отклонение — 15 баллам[1].

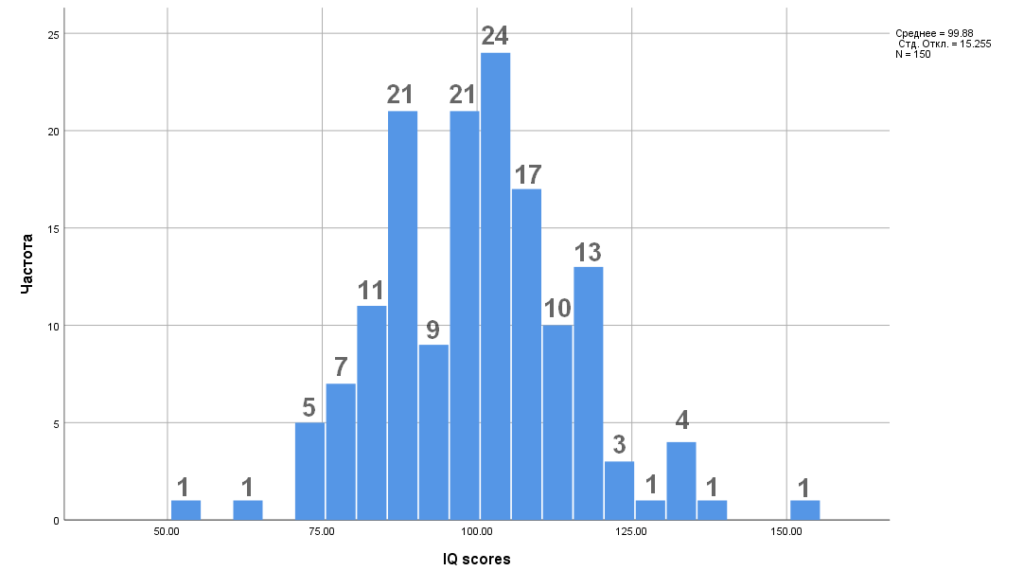
Сначала рассмотрим распределение полученных данных. Нарисуем гистограмму данных с помощью меню Графика — Устаревшие диалоговые окна — Гистограмма (Graphics — Legacy Dialogs — Histogram). Полученный результат представлен на рис. 4.3(2).

Рис. 4.3(2). Распределение баллов IQ у 150 испытуемых. Для удобства читателя мы надписали частоты появления значений над столбиками гистограммы

Можно заметить, что выборочное среднее практически совпадает со средним по генеральной совокупности, равным 100, и стандартное отклонение также слабо отличается от 15. Будем, тем не менее, пользоваться выборочными оценками для упражнений.

Теперь мы сравним выборочные частоты отклонений с теоретически предсказанным нормальным распределением.

Можно видеть, что имеется семь наблюдений меньше или равных 75. Для оценки возьмем значение 75.5, лежащее в середине отрезка (75, 76). Отклонение от выборочного среднего, измеренное в стандартных отклонениях, равно ​ (75.5 — 99.88)/15.26 = -1.53​.

В таблице распределения стандартной нормальной величины (см. 4.1.3) против 1.4 стоит значение 0.419, числу 1.43 можно считать соответствующим значение 0.41. На долю больших, чем 1.43 значений случайной величины (а значит и меньших, чем -1.43) приходится доля 0.09 от выборки. Наша выборка дает 12 из 150 (см. гистограмму), что составляет 0.08 — довольно близкое к 0.09 значение.

Упражнение 4.3(3). Проведите аналогичные оценки для значений 125, 110, 90.

Пример 4.3(4). В подпараграфе 4.2.1. рассматривается пример случайной величины — отклонения брошенного шара для боулинга от центральной кегли, измеренного в дециметрах. В файле Bouling.sav в переменной distance содержатся модельные данные такой случайной величины (результаты 1000 бросков шара). Оценим по этим данным частоту наблюдения события «шар отклонится от центральной кегли больше, чем на 1 дециметр». Для этого в SPSS можно вычислить новую переменную, которая будет принимать значение 1 при условии, что расстояние меньше единицы. Для этого надо зайти в меню Преобразование — Вычислить переменную (Transform — Compute Variable). В появившемся диалоговом окне зададим в поле Целевая переменная (Target Variable) имя новой переменной less1, а в поле Цифровое выражение (Numeric Expression) — значение переменной «1». Затем, в дополнительном окне Если (If) выберем пункт Выбрать наблюдения, удовлетворяющие условию (Include if case satisfies condition) и зададим условие ABS(distance) <= 1 (абсолютное значение переменной distance меньше или равно нулю). После выполнения расчета в таблице данных появится новая переменная less1.

Упражнение 4.3(5). Рассчитайте количество единиц в этой переменной (с помощью знакомого нам расчета частот) и сравните с теоретической вероятностью, полученной в упражнении 4.2.1(1).

Пример 4.3(6). Этот пример призван проиллюстрировать сходимость к нормальному распределению сумм независимых случайных величин В файле CenLimTh.sav содержатся результаты испытаний пяти очень разных случайных величин (переменные V1, V2, V3, V4 и V5).

Упражнение 4.3(7). Постройте гистограммы каждой из них. Вычислите их сумму  и постройте гистограмму суммы. Чтобы сравнить с нормально распределенной случайной величиной, присвойте переменной SN с помощью генератора случайных чисел, имеющих нормальное распределение N(24, 5), случайные значения и постройте гистограмму. Сравните две гистограммы.

Пример 4.3(1)j. Рассмотрим пример нормального распределения в психологическом исследовании. Допустим, мы измерили коэффициент интеллекта (по стандартной шкале IQ) у нормальных взрослых испытуемых. Модельные данные такого исследования представлены в файле NormIQ.sav. В единственной переменной IQ содержатся баллы IQ 150 испытуемых. Известно, что шкала IQ строилась так, что средний балл этого показателя равен 100, а стандартное отклонение — 15 баллам[1].

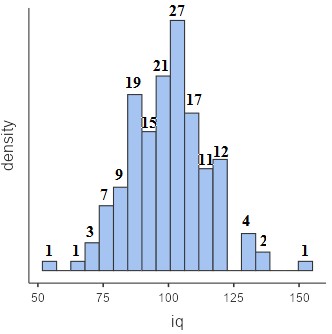
Сначала рассмотрим распределение полученных данных. Нарисуем гистограмму данных с помощью меню Analyses – Exploration – Descriptives, затем во вкладке Plots поставим галочку в квадрат Histogram. Полученный результат представлен на рис. 4.3(2)j.

Рис. 4.3(2)j. Распределение баллов IQ у 150 испытуемых. Для удобства читателя мы надписали частоты появления значений над столбиками гистограммы

Можно заметить, что выборочное среднее практически совпадает со средним по генеральной совокупности, равным 100, и стандартное отклонение также слабо отличается от 15. Будем, тем не менее, пользоваться выборочными оценками для упражнений.

Теперь мы сравним выборочные частоты отклонений с теоретически предсказанными нормальным распределением.

Можно видеть, что имеется 12 наблюдений меньше или равных 78 (правая граница столбика над числом 75). Отклонение от выборочного среднего, измеренное в стандартных отклонениях, равно (78 − 99.88)/15.26 = -1.43.

В таблице распределения стандартной нормальной величины (см. 4.1.3) против 1.4 стоит значение 0.419, числу 1.43 можно считать соответствующим значение 0.41. На долю больших, чем 1.43 значений случайной величины (а значит и меньших, чем -1.43) приходится доля 0.09 от выборки. Наша выборка дает 12 из 150 (см. гистограмму), что составляет 0.08 — довольно близкое к 0.09 значение.

Замечание 4.3(3)j. Вероятности нормального распределения для любых квантилей можно рассчитывать непосредственно в Jamovi, если установить модуль distrACTION (это делается с помощью меню modules в правом верхнем углу рабочего экрана программы). Этот модуль позволяет рассчитывать вероятности разных распределений, в том числе нормального:

В диалоговом окне нужно внести параметры нормального распределения (по умолчанию указаны стандартные параметры — математическое ожидание 0 и стандартное отклонение 1), затем выбрать тип расчёта — вероятности по квантилю (compute probability) или наоборот, квантиль по вероятности (compute quantile). Нас интересует расчёт вероятности, поэтому выбрав первый пункт при стандартных параметрах можно указать квантиль -1.43, и  мы получим следующий результат:

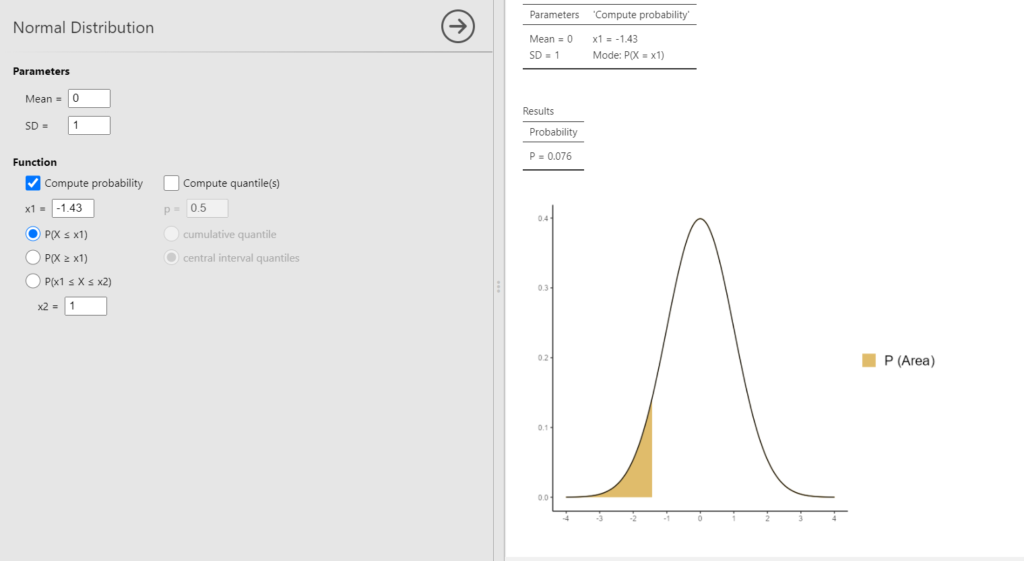
Как видим, результат расчета вероятности в (P в таблице Results) равен 0.076 и  совпадает с точностью до округления с  полученным с помощью таблиц (и даже несколько точнее)  и также близок к полученной оценке, полученной выше на основе распределения данных. Меняя варианты типов расчёта ниже поля x1, c  помощью модуля disrtACTION можно рассчитывать и вероятности типа ​\( p(N(\mu, \sigma)\geq x) \)​ или ​\( p(x_1\le N(\mu, \sigma)\le x_2) \)​. При выборе пункта Compute quantile решается обратная задача — рассчитывается квантиль, соответствующий заданной вероятности (по умолчанию — двухсторонний). Например, если задать вероятность 0.95б то будет рассчитан двухсторонний квантиль нормального распределения, отсекающий с двух сторон хвосты с площадью 0.025 (то есть в сумме — 0.05).

Упражнение 4.3(4)j. Проведите аналогичные оценки для значений 125, 110, 90.

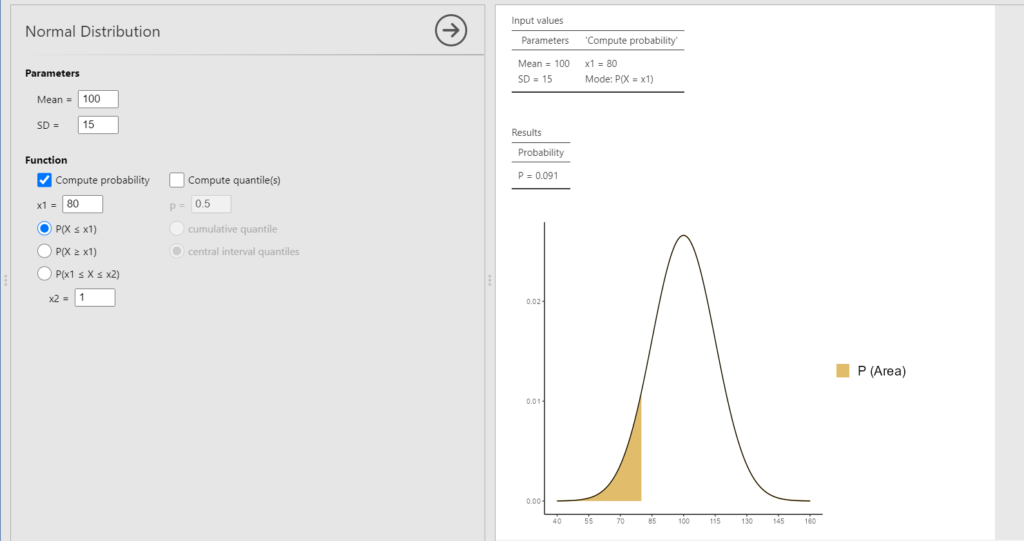
Замечание 4.3(5)j. С помощью модуля distrACTION можно оценивать вероятности не переводя исходные данные в стандартное значение, указав значение полей Mean и SD равными математическому ожиданию и стандартному отклонению теоретического нормального распределения (установленные априорно или оцененные по выборке с помощью выборочного среднего и стандартного отклонения). Например, при математическом ожидании IQ 100 и стандартном отклонении 15 оценка вероятности ​\( p(N(100, 15) \leq 80) \)​ будет выглядеть так:

Пример 4.3(6)j. В подпараграфе 4.2.1. рассматривается пример случайной величины — отклонения брошенного шара для боулинга от центральной кегли, измеренного в дециметрах. В файле Bouling.sav  в переменной distance содержатся модельные данные такой случайной величины (результаты 1000 бросков шара). Оценим по этим данным частоту наблюдения события «шар отклонится от центральной кегли больше, чем на 1 дециметр». Для этого в Jamovi можно вычислить новую переменную, которая будет принимать значение 1 при условии, что расстояние меньше единицы. Для этого надо зайти в меню Data — Compute. В появившемся диалоговом окне зададим в верхнем поле (Computed Variable) имя новой переменной less1, а в правом нижнем окне формулу IF(ABS(distance)<1, 1, 0) — программа для каждой строки проверит, лежит ли значение переменной distance в интервале от -1 до 1, и в случае утвердительного ответа присвоит переменной less1 значение 1, в противном случае 0). После выполнения расчета в таблице данных появится новая переменная less1.

Упражнение 4.3(7)j. Рассчитайте количество единиц в этой переменной (с помощью знакомого нам расчета частот) и сравните с теоретической вероятностью, полученной в упражнении 4.2.1.

Пример 4.3(8)j. Этот пример призван проиллюстрировать сходимость к нормальному распределению сумм независимых случайных величин В файле CenLimTh.sav содержатся результаты испытаний пяти очень разных случайных величин (переменные V1, V2, V3, V4 и V5).

Упражнение 4.3(9). Постройте гистограммы каждой из них. Вычислите их сумму S = V1+V2+V3+V4+V5 и постройте гистограмму суммы. Чтобы сравнить с нормально распределенной случайной величиной, присвойте переменной SN с помощью генератора случайных чисел, имеющих нормальное распределение N(23, 5), случайные значения и постройте гистограмму (при вычислении с помощью пункта Data — Compute вставьте в правое нижнее окно выражение NORM (23, 5)). Сравните две гистограммы.

Пример 4.3(1)r. Рассмотрим пример нормального распределения в психологическом исследовании. Допустим, мы измерили коэффициент интеллекта (по стандартной шкале IQ) у нормальных взрослых испытуемых. Модельные данные такого исследования представлены в файле NormIQ.sav. В единственной переменной IQ содержатся баллы IQ 150 испытуемых. Известно, что шкала IQ строилась так, что средний балл этого показателя равен 100, а стандартное отклонение — 15 баллам[1].

Сначала рассмотрим распределение полученных данных. Загрузив данные в таблицу data_IQ нарисуем гистограмму данных с помощью функции hist, указав в качестве дополнительного аргумента breaks число интервалов, для которых будут рассчитаны и отображены частоты, а также подписав заголовок (main) и оси (xlab и ylab).

library(foreign)
data_IQ <- read.spss("NormIQ.sav", to.data.frame = T, reencode = "utf8")
hist(data_IQ$iq, breaks = 20, main = "Частотный график распределения IQ", xlab = "IQ", ylab = "Частота")

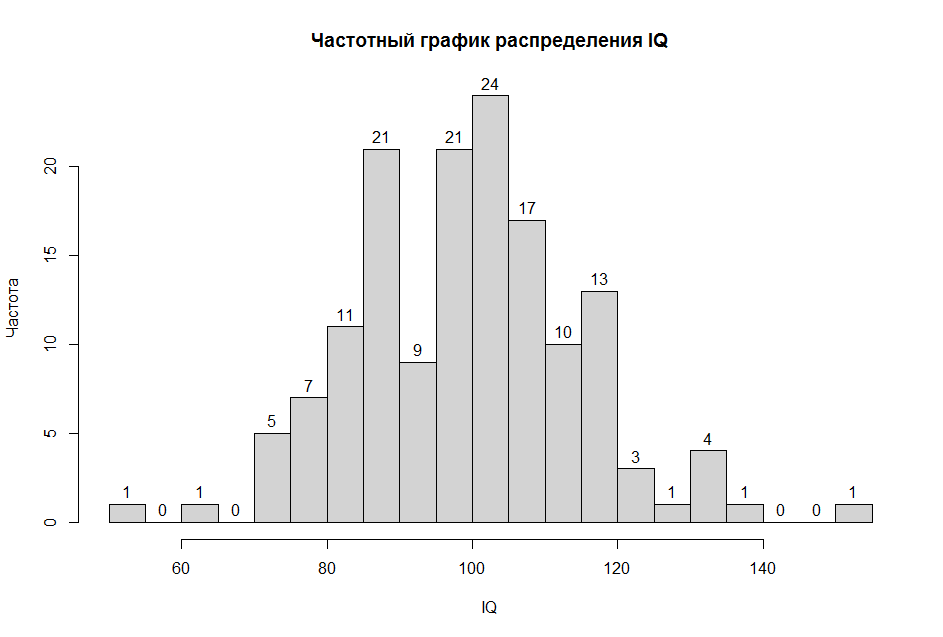
Полученный результат представлен на рис. 4.3(2)r.

Рис. 4.3(2). Распределение баллов IQ у 150 испытуемых. Для удобства читателя мы надписали частоты появления значений над столбиками гистограммы[2]

Также рассчитаем описательную статистику для этой переменной с помощью функции describeиз пакета psych:

require("psych")
describe(data_IQ$iq)

vars   n  mean    sd median trimmed   mad min max range skew kurtosis   se
X1    1 150 99.88 15.26   99.5   99.72 15.57  53 151    98 0.15     0.44 1.25

Можно заметить, что выборочное среднее практически совпадает со средним по генеральной совокупности, равным 100, и стандартное отклонение также мало отличается от 15. Будем, тем не менее, пользоваться выборочными оценками для упражнений.

Теперь мы сравним выборочные частоты отклонений с теоретически предсказанными нормальным распределением.

Можно видеть, что имеется семь наблюдений меньше или равных 75. Для оценки возьмем значение 75.5, лежащее в середине отрезка (75, 76). Отклонение от выборочного среднего, измеренное в стандартных отклонениях, равно (75.5 — 99.88)/15.26 = -1.53.

В таблице распределения стандартной нормальной величины (см. 4.1.3) против 1.5 стоит значение 0.433, числу 1.53 можно считать соответствующим значение 0.44. На долю больших, чем 1.53 значений случайной величины (а значит и меньших, чем -1.53) приходится доля 0.06 от выборки. Наша выборка дает 7 из 150 (см. гистограмму), что составляет 0.047 — довольно близкое к 0.06 значение.

Упражнение 4.3(3)r. Проведите аналогичные оценки для значений 125, 110, 90.

Пример 4.3(4)r. В подпараграфе 4.2.1. рассматривается пример случайной величины — отклонения брошенного шара для боулинга от центральной кегли, измеренного в дециметрах. В файле Bouling.sav в переменной distance содержатся модельные данные такой случайной величины (результаты 1000 бросков шара). Загрузив данные в таблицу data_bouling, оценим по этим данным частоту наблюдения события «шар отклонится от центральной кегли больше, чем на 1 дециметр». В R это можно сделать, разными способами. Самый очевидный, но относительно длинный вариант – это рассчитать новую переменную, которая будет принимать значение 1 при условии, что расстояние меньше единицы. Для этого зададим новую переменную в таблице данных и присвоим её значение 1 при выполнении условия, что абсолютной значение переменной distance (вычисляемое с помощью функции abs) меньше либо равно единице. Затем посчитаем частоту встречаемости единицы, а для получения относительной частоты (статистической оценки вероятности) поделим на общее число наблюдений (вычисляемое как число строк в таблице с помощью функции nrow):

data_bouling$less1 <- NA
data_bouling$less1[abs(data_bouling$distance) <= 1] <- 1
table(data_bouling$less1)/nrow(data_bouling)
Полученный результат – 0.671.

Тот же результат можно получить, использовав следующую более компактную конструкцию:

prop.table(table(abs(data_bouling$distance) <= 1))

и получить следующий результат:

FALSE  TRUE
0.329 0.671

Логика использованной конструкции такова: выражение abs(data_bouling) <= 1возвращает логический вектор, состоящий из значений TRUE и FALSE в зависимости от выполнения условия, затем рассчитывается таблица абсолютных частот с помощью функции table, а затем – относительные частоты с помощью функции prop.table.

Упражнение 4.3(5)r. Сравните полученную частоту с теоретической вероятностью, полученной в упражнении 4.2.1(1).

Пример 4.3(6)r. Этот пример призван проиллюстрировать сходимость к нормальному распределению сумм независимых случайных величин В файле CenLimTh.sav содержатся результаты испытаний пяти очень разных случайных величин (переменные V1, V2, V3, V4 и V5).

Упражнение 4.3(7)r. Постройте гистограммы каждой из них. Вычислите их сумму и постройте гистограмму суммы. Чтобы сравнить с нормально распределенной случайной величиной, создайте новую переменную SN  и заполните её значениями с помощью генератора случайных чисел, имеющих нормальное распределение N(24, 5). Это можно сделать с помощью функции rnorm(n, mean, sd), где n – требуемая длина вектора, mean – математическое ожидание, а sd – стандартное отклонение требуемого нормального распределения (по умолчанию равны 0 и 1 соответственно). Таким образом, надо использовать следующую конструкцию (при условии, что таблица называется data_frame):

data_frame$SN <- rnorm(nrow(data_frame, 24, 5).

Постройте гистограмму полученной переменной. Сравните её с гистрограммой суммы переменных V1-V5.