При расчете вероятностей по «классическому» определению мы используем отношение количества благоприятных исходов к общему количеству возможных исходов. Здесь мы научимся считать эти количества исходов, как бы велики они ни были. Для того чтобы считать биномиальные (см. подпараграф 2.1.4) вероятности, мы должны освоить комбинаторные понятия и соответствующие им формулы.
Наш первый модельный пример, с которым будут соотноситься другие примеры, таков.
Пример П6.1(1). Сколькими способами можно разложить k пронумерованных шаров в n пронумерованных корзин (\( n≥k \) ) так, чтобы в каждой корзине оказалось не больше одного шара?
Решим задачу сначала для \( n=4,k=2 \). Всего возможно 12 различных размещений (рис. П6.1(2), справа). Следующее рассуждение показывает, почему вариантов именно 12.
Первый шар мы можем положить в любую из четырех имеющихся корзин, после чего второй шар может быть размещен в любой из оставшихся трех корзин. Можно представить выбор в виде дерева, каждая ветка которого оканчивается одним из вариантов размещения (рис. П6.1(2), слева).
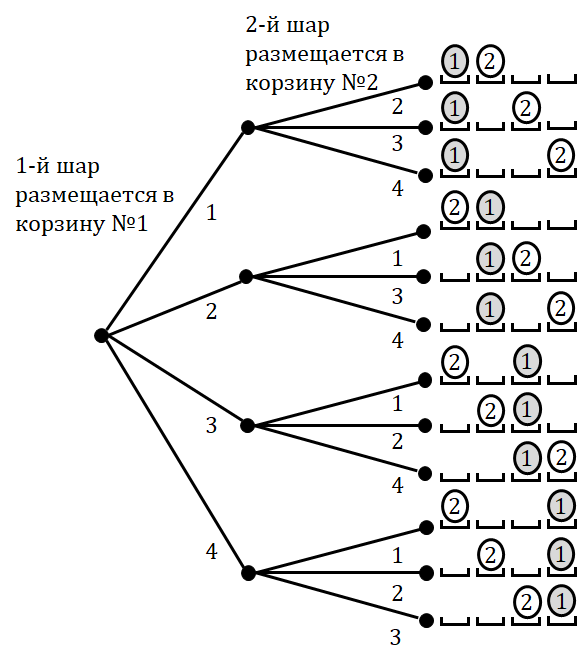Рис. П6.1(2). Размещения двух различимых шаров по четырем корзинам
Это рассуждение легко распространяется на случай произвольных n и k:
первый шар может быть положен в любую из n корзин,
второй шар — в любую из оставшихся корзин,
третий шар — в любую из оставшихся корзин,
…
k-й шар в любую из оставшихся \( n-(k-1) \) корзин.
Всего получается \( n\cdot(n-1)⋅(n-2)⋅…⋅(n-(k-1)) \) размещений.
Количество размещений k элементов в n ячеек обозначается \( A^k_n \). Мы вывели формулу числа размещений:
\[ A_n^k=n⋅(n-1)⋅(n-2)⋅…⋅(n-(k-1))=n⋅(n-1)⋅(n-2)⋅…⋅(n-k+1). \]
Если \( n=k \), то последняя строка будет оканчиваться словами «в любую из одной корзины». Этот последний частный случай размещений называется перестановками совокупности n элементов. Количество перестановок n элементов равно в точности n!. Напомним, что \( n!=1⋅2⋅…⋅n \) — (читается «эн факториал») есть произведение натуральных чисел от 1 до n.
Следующий вопрос, который вплотную подводит нас к формуле бинома Ньютона, звучит так: сколькими способами можно выбрать из n различимых предметов k штук?
Пример П6.2(1). Сколькими способами можно выбрать из четырех пронумерованных корзин две?
Мы свяжем этот пример с предыдущим следующим образом: выбранные корзины будем отмечать тем, что положим в них шары. Тот же рис. П6.1(2) дает первый шаг решения — в первой строке обозначен выбор первой и второй корзин, во второй строке — первой и третьей и т.д.
Однако можно заметить, что каждый выбор пары корзин встречается в списке из двенадцати размещений дважды. Первый выбор можно найти также в четвертой строке, второй выбор — в шестой и т.д. В случае размещений нам существенно, какой шар оказался в данной корзине, в случае сочетаний — не существенно.
Это значит, что каждый случай выбора пары корзин считается столько раз, сколькими способами можно поменять местами шары в уже отмеченных корзинах. В данном случае таких перемен мест (перестановок) всего две.
Итак, выбрать две корзины из четырех можно шестью способами.
Пример П6.2(2). Сколькими способами можно выбрать из четырех пронумерованных корзин три?
Решим сначала задачу о размещениях. По нашей формуле имеется 24 способа размещения трех шаров в четырех корзинах: каждое из приведенных на рис. П6.1(2) размещений двух шаров может быть дополнено двумя разными размещениями третьего шара в любую из оставшихся пустыми корзин.
Рассмотрим теперь, сколько раз мы считаем один и тот же выбор корзин, различая размещения разных шаров по одним и тем же корзинам (рис. П6.2(3)).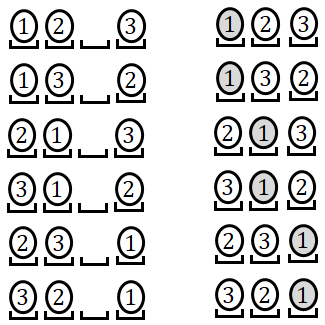
Рис. П6.2(3). Расчет количества перестановок для формулы числа сочетаний
Рассмотрим, например, размещение, изображенное на рис. П6.2(3) в первой строке слева. Под ним перечислены все возможные размещения в тех же самых корзинах, но с другим порядком шаров. В правой колонке приведены соответствующие перестановки из трех элементов. Понятно, что эти же самые перестановки будут соответствовать размещениям трех шаров в любых фиксированных трех корзинах. Это значит, что каждый выбор трех корзин из четырех считается шесть раз в формуле числа размещений. Таким образом, три корзины из четырех можно выбрать \( \frac{24}{6}=4 \) способами.
Замечание П6.2(4). Отметим интересное равенство: точно так же четырем равно количество возможных выборов из четырех корзин по одной. Это очень важное совпадение объясняется тем, что каждый выбор трех корзин оставляет одну корзину «невыбранной», и, наоборот, каждому выбору одной корзины можно поставить в соответствие выбор дополнительных к ней трех. Следовательно, сколькими способами можно выбрать одну корзину из четырех, столькими способами можно выбрать и три из четырех.
Теперь мы можем решить вопрос о выборе из совокупности в общем случае. Для того чтобы посчитать, сколькими способами можно выбрать k корзин из различимых n, надо сначала вычислить количество размещений k различимых шаров в n корзинах и полученное число поделить на количество перестановок различимых k шаров, или, что то же самое, на количество размещений k шаров в k корзинах. Результат, который называется числом сочетаний из n элементов по k и обозначается \( C_n^k \), запишем сначала в следующем виде:
\[ С_n^k=\frac{n⋅(n-1)⋅(n-2)⋅…⋅(n-(k+1))}{k\cdot(k-1)\cdot(k-2)\cdot…\cdot2\cdot1} \]
Эту формулу проще запомнить, если домножить и числитель, и знаменатель на \( (n-k)! \), тогда в числителе окажется n! и формула примет вид
\[ С_n^k=\frac{n⋅(n-1)⋅(n-2)⋅…⋅(n-(k+1))×(n-k)⋅(n-k-1)⋅…⋅2⋅1}{k⋅(k-1)⋅(k-2)⋅…⋅2⋅1×(n-k)⋅(n-k-1)⋅…⋅2⋅1}=\frac{n!}{k!⋅(n-k)!} \].
Замечание П6.2(5). Из последнего варианта формулы сразу понятно, что \( C_n^k=C_n^{(n-k)} \), поскольку если \( a=n-k \), то \( n-a=k \) и знаменатели в обеих формулах совпадут. На уровне нашей подразумеваемой интерпретации в терминах выбора корзин этому равенству соответствует следующий аргумент, повторяющий приведенный в предыдущем замечании: если мы выбрали k корзин из n, то тем самым мы выбрали и дополнительные, оставшиеся корзин. Всякому выбору k корзин соответствует единственный выбор n−k корзин.
Рассмотрим выражение \( (p+q)^n \) (оно называется биномом Ньютона n-й степени). Что получится, если раскрыть скобки? Начнем с выражения \( (p+q)^4=(p+q)(p+q)(p+q)(p+q) \). После раскрытия скобок получатся 16 слагаемых, которые мы не будем сейчас выписывать, потому что нам гораздо важнее сформулировать правило перечисления этих слагаемых. Заметим, что каждое слагаемое — произведение четырех сомножителей — получается так: из каждой из четырех скобок выбирается p или q, затем они перемножаются.
Для того чтобы не потерять ни одного слагаемого, будем использовать так называемое двоичное дерево (рис. П6.3(1)). Каждая ветка дерева заканчивается произведением p и q, которое получается по следующему правилу: если на первом шаге от корня дерева выбирается ветка p, то p становится первым членом произведения, если q, то первым членом произведения становится q. На втором шаге аналогично, в зависимости от выбора ветки, добавляется второй сомножитель p или q. Так же осуществляется выбор на третьем и четвертом шагах.
Легко видеть, что общее количество концевых вершин \( 16=2^4 \) — два в степени, равной степени бинома. Наш следующий вопрос, сколько слагаемых из этих шестнадцати после перегруппировки сомножителей окажутся равными \( p^2 q^2 \). Рис. П6.3(1) показывает, что мы можем дать ответ на этот и подобные вопросы без непосредственного счета — достаточно установить соответствие между каждым из произведений, содержащих p и q во второй степени, и элементами нашей «корзиночной модели»: каждому такому произведению соответствует выбор каких-то двух корзин из четырех. На рисунке справа, рядом с произведениями, содержащими квадраты p и q, изображены соответствующие этим произведениям выборы корзинок. Сколько способов выбора пары корзинок из четырех, столько будет членов, содержащих квадраты p и q, в биноме после раскрытия всех скобок.
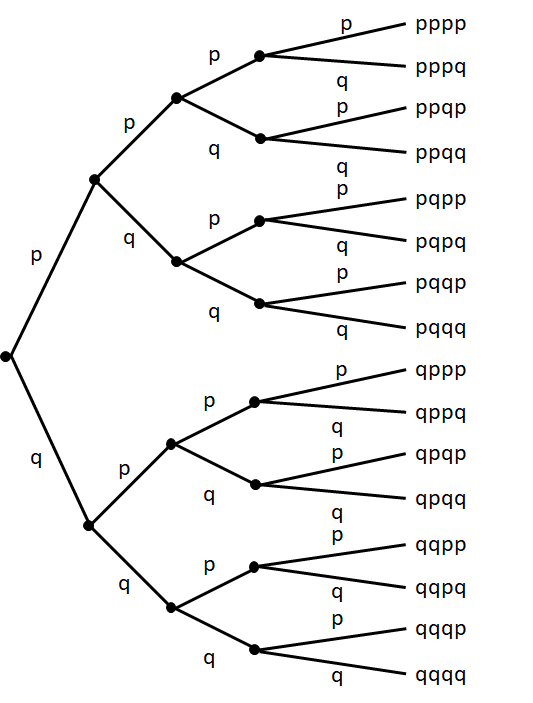Рис. П6.3(1). Дерево слагаемых бинома Ньютона четвертой степени
Совершенно аналогично ведется рассуждение в общем случае: если нам надлежит раскрыть скобки в выражении \( (p+q)^n \), то слагаемых, содержащих \( p^k q^{(n-k)} \) будет столько, сколько существует различных выборов k (или, что то же самое, \( n-k \)) корзин из n возможных.
Таким образом,
\[ (p+q)^n=C_n^0 p^n q^0+C_n^1 p^{(n-1)} q^1+C_n^2 p^{(n-2)} q^2+…+C_n^{(n-1)} p^1 q^{(n-1)}+C_n^n p^0 q^n \]
В этой формуле присутствует член \( C_n^0 \), который словами может быть описан по аналогии со своими соседями: сколькими способами можно выбрать 0 корзин из n. При всей сомнительности такой формулировки, из алгебраической формулы понятно, что \( C_n^0=1 \).
По крайней мере, нет никаких соображений, по которым выбрать из n корзин 0 можно каким-то другим, отличным от единицы количеством способов. В подобных ситуациях математики принимают соглашение[1] считать \( C_n^0 \) равным единице, а заодно равным единице и 0!, который входит в формулу
\[ С_n^0=\frac{n!}{n!\cdot0!} \]
Коэффициенты \( C_n^k \) входящие в формулу бинома Ньютона, называются биномиальными коэффициентами.
[1] Это соглашение никак нельзя считать произвольным, поскольку дальнейшее использование показывает, что соглашение дает реальные удобства, причем не только в той области, в которой первоначально были введены такие конвенциональные определения, а противоречий или других каких-то неприятностей не обнаруживается. Читатель может продумать этот комментарий на примере хорошо ему известной «конвенции» считать произведение отрицательных чисел положительным числом. Такой конвенции невозможно придумать приемлемую альтернативу.