10.2.1. Основные идеи и примеры
Большинство независимых переменных, которые используются в психологии, так или иначе коррелируют между собой. Это означает, что по причинам, рассмотренным в предыдущем параграфе, во множественной регрессии исследователь может основывать свои выводы на показателях значимости модели и коэффициенте детерминации, но ограничен при оценке вклада (эффекта)[1] каждой из независимых переменных. Дальнейшее развитие множественного регрессионного анализа привело к появлению трех новых методов, которые позволили проверять некоторые (довольно узкие) гипотезы о вкладах независимых переменных, с минимальным риском искажений из-за мультиколлинеарности независимых переменных. Все эти методы основаны на проведении нескольких регрессионных анализов и сопоставлении между собой их результатов.
Иерархический регрессионный анализ направлен на проверку гипотезы о независимом вкладе одной из переменных в зависимую переменную, после статистического контроля других переменных. Для иллюстрации вернемся к примеру со «временем выдержки» дошкольников и последующей успеваемостью (подпараграф 9.1.4). Понятно, что успеваемость зависит и от исходного уровня интеллекта, который, вероятнее всего, связан со «временем выдержки» дошкольника наедине с конфетой. Критики могут предположить, что полученная нами связь «время выдержки — успеваемость» полностью объясняется интеллектом дошкольников, и эксперимент с отсрочкой вознаграждения не добавляет нового к нашему знанию об успеваемости. Изменим психологическую гипотезу так, чтобы она отвечала иерархическому регрессионному анализу: умение дошкольника отсрочить вознаграждение связано с последующей успеваемостью, после статистического контроля (или независимо от) его уровня интеллекта. В отличие от множественной регрессии, в иерархической регрессии заданы уровни независимых переменных: переменные первого уровня –- те, эффект которых мы хотим проконтролировать, и переменные второго уровня — те, эффект которых мы хотим установить[2] (рис. 10.2.1(1)).
Рис. 10.2.1(1). Пример модели иерархического регрессионного анализа (НП — независимая переменная, ЗП — зависимая переменная)
Анализ медиации применяется для установления прямого и косвенного (непрямого) эффекта влияния независимой переменной на зависимую. Гипотеза звучит следующим образом: по крайней мере, часть эффекта влияния независимой переменной в отношении зависимой непрямая, а проходит через третью переменную-медиатор. Например, вряд ли «время выдержки» напрямую определяет успеваемость через несколько лет — разумно предположить, что умение ждать вознаграждения в дошкольном возрасте помогает чему-то, что позже определяет успеваемость, — скажем, концентрации внимания в случае монотонной деятельности в классе. Общий эффект независимой переменной на зависимую состоит из двух эффектов — прямого и косвенного (рис. 10.2.1(2)). При этом косвенный эффект состоит в том, что дети, которые дольше не берут конфету, позже лучше и дольше сосредотачиваются на предметах в школе, и именно этот навык помогает их успеваемости. В отличие от множественной регрессии, в анализе медиации установлена последовательность связей между переменными — что и через какие переменные мы пытаемся объяснить. В отличие от иерархической регрессии, в центре внимания здесь не «прирост» после добавления переменной (ведь общий эффект не изменится с добавлением медиатора), а содержание общего эффекта. Как мы покажем в подпараграфе 10.2.3, это означает, что если в иерархической регрессии ключевой интерес представляют коэффициенты детерминации и F-отношения, а также значимость модели, то в анализе медиации — коэффициенты регрессионного уравнения и их значимость.
Рис. 10.2.1(2). Пример модели анализа медиации
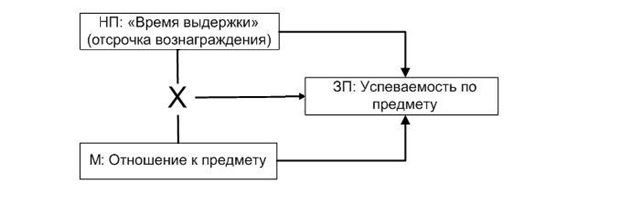
Анализ модерации используется для проверки гипотезы о различиях во вкладе независимой переменной в зависимую при разных уровнях переменной-модератора. Например, можно предположить, что «время выдержки» у дошкольников по-разному сказывается на успеваемости в отношении конкретного предмета (скажем, русского языка и литературы или математики) в зависимости от отношения к этому предмету. Если ребенку предмет нравится, ему интересно, то для освоения предмета ему не требуется заставлять себя длительно концентрироваться на уроке и время, которое он может ждать награждения, не столь важно. Если же предмет не нравится, возможности саморегуляции и терпение крайне важны — без них успеваемость вряд ли будет высока. На рис. 10.2.1(3) показан пример такой модели: всего в ней возможно три эффекта. Во-первых, «время выдержки» может способствовать успеваемости по всем предметам, как любимым, так и не любимым (основной эффект независимой переменной). Во-вторых, очевидно, что отношение к предмету само по себе связано с успеваемостью (основной эффект модератора). В-третьих, «время выдержки» может более сильно сказываться на успеваемости у тех детей, которые данный предмет не любят, и слабее — у тех, для кого этот предмет любимый (эффект взаимодействия независимой переменной и модератора). В анализе модерации исследователя интересует именно этот эффект взаимодействия — эффект модерации. Внимательный читатель, вероятно, заметил, что задачи анализа модерации те же, что и в двухфакторном дисперсионном анализе — в обоих методах речь идет о разделении основных эффектов и эффекта взаимодействия, однако задача эта решается разными способами. В дисперсионном анализе мы могли сравнить внутригрупповые и межгрупповые дисперсии; в регрессионном анализе нам придется создать новую переменную, описывающую взаимодействие независимой переменной и модератора, и проверить, добавляет ли она что-то к объяснению дисперсии зависимой переменной. В отличие от множественной регрессии, анализ модерации сосредоточен на поиске эффектов взаимодействия. Как мы покажем в подпараграфе 10.2.4, по процедуре анализ модерации проводится так же, как и иерархическая регрессия — с той разницей, что на шаге 2 добавляется не другая независимая переменная, а переменная, созданная из переменных шага 1. От анализа медиации анализ модерации отличается тем, что задачей является не разделение прямого и косвенного эффектов независимой переменной, а поиск различий в ее эффектах в зависимости от модератора.
Рис. 10.2.1(3). Пример модели анализа модерации
Далее мы кратко изложим математическую суть иерархического регрессионного анализа и анализа модерации. Подробное описание анализа медиации (и модерации тоже) можно найти на сайте разработчиков современного варианта проведения этих методов Кристофера Причера и Эндрю Хейеса (http://www.quantpsy.org/medn.htm и http://afhayes.com/), которые содержат не только материалы, но и программы (в том числе для SPSS), позволяющие рассчитать косвенный эффект и оценить его значимость.
10.2.2. Иерархическая регрессия (расчеты)
Процедура иерархической регрессии требует проведения анализа несколько раз и сопоставления каждого следующего шага с предыдущим. Для примера на рис. 10.2.1(1) таких шага два: на первом шаге проводится простая линейная регрессия для выявления связи «IQ — успеваемость», на втором шаге — множественная регрессия с двумя независимыми переменными IQ и «время выдержки». Результаты сравниваются, т.е. и нуль-гипотеза, и альтернативная гипотеза являются гипотезами о значимости различий: «изменение объясняемой моделью дисперсии зависимой переменной на шаге 2 не отличается от нуля» и «изменение объясняемой моделью дисперсии зависимой переменной на шаге 2 отличается от нуля» соответственно. Исходные данные и основные формулы остаются неизменными: измерения заданы тройками значений:
\[ (x_1,y_1,z_1),…,(x_n,y_n,z_n). \]
а формула регрессии
\[ z=a_x+a_y+b. \]
На первом шаге регрессии мы полагаем , что превращает формулу в уравнение простой линейной регрессии. Иными словами, мы ищем наилучшую в смысле наименьших квадратов плоскость, параллельную оси y. На втором шаге мы рассчитываем, какое «улучшение» в отношении наименьших квадратов дает возможность расположить плоскость «под углом» к оси y. Изменение коэффициента детерминации характеризует изменение (улучшение) процента дисперсии зависимой переменной, объясняемой моделью (относительно общей дисперсии):
\[ ΔR^2=R_2^2-R_1^2=\frac{S_{model1}-S_{model2}}{S_{total}} \]
Заметим, что общую дисперсию зависимой переменной теперь можно записать двумя способами: как сумму дисперсии, объясняемой моделью 1, и ее дисперсии ошибки и как сумму дисперсии, объясняемой моделью 2, и ее дисперсии ошибки. Для суммы квадратов (без деления на число степеней свободы):
\[ S_{total}=S_{model1}+S_{error1}=S_{model2}+S_{error2} \]
F-отношение для изменения модели аналогично обычному F-отношению для регрессии, которое обсуждалось выше: но в числителе теперь стоит разность сумм квадратов двух моделей, деленных на разность их степеней свободы, а знаменатель считается по второй модели. Другими словами, F-отношение для изменения модели описывает «выигрыш» в объясняемой дисперсии относительно дисперсии ошибки:
\[ \Delta F=\frac{(S_{model2}-S_{model1})/(df_2-df_1)}{S_{error2}/df_{error2}} \]
Значимость изменения модели можно теперь оценить как вес отсекаемого ΔF хвоста распределения Фишера, первая степень свободы которого равна \( df_2-df_1 \) — разница между числом параметров во второй и первой моделях, а вторая \( df_{error2} \) — общее число испытуемых минус число независимых переменных минус 1. Для нашего примера \( df_2-df_1=2-1=1 \), а \( f_{error2}=n-3 \). Значимость изменения модели позволяет сделать выбор между нуль-гипотезой и альтернативной гипотезой, отвечая на вопрос о том, можно ли считать, что «время выдержки» важно для успеваемости, вне зависимости от исходного уровня интеллекта в дошкольном возрасте. Проблема мультиколлинеарности независимых переменных в иерархическом регрессионном анализе остается, но она перестает влиять на вывод: ведь вся общая дисперсия между независимыми переменными, которая разделена у них с зависимой переменной, приписывается переменным первого уровня («контролируется»). А определяется уникальный вклад переменной второго уровня. Регрессионные коэффициенты в иерархической регрессии не являются центральным предметом интереса для исследователя.
10.2.3. Анализ модерации (расчеты)
На рис. 10.2.1(3) приведен пример, в котором мы предполагаем, что вклад «времени выдержки» в успеваемость выше у тех, кто не любит данный предмет, и ниже у тех, кто любит данный предмет. Это означает, что, если мы рассматриваем тех, кому предмет не нравится, облако точек-измерений на графике «время выдержки — успеваемость» будет более вытянуто вдоль некоторой прямой (связь будет сильнее, а наше предсказание — точнее), а если тех, кому нравится, — оно будет более округлым. Во всех случаях анализа модерации речь идет о том, что линии существенно различаются при разных уровнях модератора.
Во множественной регрессии по тройкам значений \( (x_1,y_1,z_1),…,(x_n,y_n,z_n). \) в трехмерном пространстве подбирается плоскость, лежащая ближе всего к точкам, координаты которых заданы этими наборами значений. В анализе модерации мы, говоря образно, «разрешаем» этой плоскости быть изогнутой, иметь седловину — и оцениваем, дает ли нам это разрешение «выигрыш» в объяснении дисперсии зависимой переменной. Нулевая гипотеза в данном случае такова: эффект независимой переменной в отношении зависимой не различается на разных уровнях (при разных значениях) модератора. Альтернативная гипотеза утверждает, что различие есть. Новая переменная, характеризующая модерацию, несет в себе информацию о сочетании разных значений независимой переменной и модератора: в случае если у испытуемого крайне высокие или крайне низкие значения, показатель по этой переменной должны быть высок. Если же одно из значений крайне низкое, а другое — крайне высокое, показатель должен быть низок. В нашем примере на одном полюсе оказываются школьники, «умеющие ждать и любящие предмет», а также «не умеющие ждать и не любящие предмет», а на другом — «умеющие ждать и не любящие предмет» и «не умеющие ждать, но любящие предмет»[3].
Для вычисления новой переменной независимая переменная и модератор центрируются, а затем для каждого испытуемого (измерения) два его значения по этим переменным перемножаются. Затем проводится иерархическая регрессия: на первом ее шаге в модель добавляются центрированные независимая переменная и модератор, на втором — переменная их взаимодействия (говорят: «их продукт»). Изменение в проценте объясняемой дисперсии зависимой переменной и значимость изменения позволяют выбрать между нулевой гипотезой и альтернативой.
Центрирование необходимо, чтобы избежать проблемы мультиколлинеарности: если перемножить сырые значения, новая переменная может коррелировать с исходными и добавление ее во множественную регрессию исказит регрессионные коэффициенты независимой переменной и модератора (см. параграф 10.1). Коэффициенты детерминации \( R^2 \) и значимость модели и ее изменения останутся теми же, но интерпретировать результаты будет сложно из-за нестабильности коэффициентов. Центрируя переменные, мы достигаем того, что они не коррелируют со своим продуктом (переменной взаимодействия). Уравнение регрессии в анализе модерации выглядит следующим образом:
\[ z=a_x x+a_y y+a_{xy} xy+b. \]
При этом коэффициент \( a_x \) — это то, насколько изменение x на единицу приводит к изменению z, когда y равен нулю (поскольку мы центрировали переменные, нуль — среднее значение). Т.е. при увеличении времени выдержки дошкольника на единицу при нейтральном (среднем) отношении к предмету успеваемость увеличивается на \( a_x \).
Упражнение. Самостоятельно опишите, что означает \( a_y \).
Коэффициент \( a_{xy} \) описывает то, насколько меняется эффект x при изменении y от 0 до 1. Это видно, если переписать уравнение регрессии:
\[ z=(a_x+a_{xy} y)x+a_y y+b. \]
Для удобства понимания и иллюстрации полученного эффекта взаимодействия обычно применяют простые регрессии: разделяя испытуемых на группы с разными уровнями по переменной-модератору (например, любящих предмет школьников, не любящих и относящихся к нему нейтрально) и затем проводя анализ отдельно в этих группах (а графически: рисуя несколько прямых на плоскости). В третьем параграфе мы приведем пример такой иллюстрации.
10.2.4. Медиация, модерация и опосредствование
Медиацию и модерацию нередко путают — в русском языке еще и из-за того, что результаты обоих методов интерпретируется в исследованиях как «опосредствование». Медиацию применяют, если задача — установить природу некоторого эффекта независимой переменной на зависимую. Это поиск «путей»[4], по которым происходит эффект, который можно выразить предложением: «Эффект X в отношении Y обусловлен его общей дисперсией с M». Эффект модерации — это эффект взаимодействия между независимыми переменными, который можно описать так: «Эффект X в отношении Y различается при разных значениях M».
Говоря метафорически, медиатором можно назвать провод между лампочкой и розеткой — именно по нему идет ток, и без этого лампочка не зажжется, а модератором — выключатель. Когда он выключен, связи между розеткой и лампочкой нет, когда включен — есть. Действия психолога в анализе медиации схожи с работой электрика, который в пучке проводов ищет единственный работающий провод («путь», благодаря которому лампочка горит). Анализ модерации же сродни проверке выключателя: изменяется ли освещение, если на него нажать?
Ранее для того, чтобы различить гипотезы о медиации и модерации в своих исследованиях, предлагалось проверить корреляции между переменными. Так, в случае медиации все три переменные коррелируют (чтобы объяснить связь независимых и зависимой переменных, нужно, чтобы она была), а модерацию часто применяют именно в тех случаях, когда ожидаемой корреляции нет или она различна в разных работах. «Эмпирическая» постановка задач для обработки данных действительно имеет место в науке (например, получив связь между независимыми и зависимой переменными, исследователь задается вопросом, чем она объясняется, а отсутствие ожидаемой связи приводит к размышлениям, не зависит ли эта связь от каких-то других переменных). Однако это «правило» применимо далеко не всегда. Косвенный эффект (эффект медиации) может быть предметом исследования и достичь приемлемой значимости, даже если общий и/или прямой эффекты независимой переменной приемлемой значимости не достигают[5]. Модерация также может проводиться и в случае, если связь между независимыми и зависимой переменными установлена.
Обратим внимание, что ни медиация, ни модерация не означают причинно-следственной связи — что характерно для любых методов обработки данных. Делая психологический вывод из исследования, медиацию нередко интерпретируют как свидетельство в пользу механизма действия независимой переменной (термин «опосредствование» употребляется тогда в смысле «путь» и «механизм»), а модерацию — как доказательство разницы в механизмах («опосредствование» в смысле «различий в механизмах», «различий в способах действия»). Однако вывод этот не относится к сфере статистики и не гарантируется ею; теория, дизайн и процедура исследования помогают исследователю быть более или менее уверенным и обосновать свои выводы. Интересно, что некоторые специалисты по статистике предлагают употреблять термин «медиация», только если речь идет об экспериментальном или лонгитюдном исследовании и все переменные измерены как минимум трижды[6] , а в других случаях говорить только о косвенном эффекте.
>> следующий параграф>>
[1] Далее мы используем термины «эффект» и «вклад» независимых переменных в зависимую, говоря о регрессионных коэффициентах и их значимости, для того, чтобы избежать иллюзии причинности, описанной выше (и которая создается при использовании слов «влияние» и «предсказание» в регрессионном анализе).
[2] Уровней переменных может быть больше: на каждом следующем шаге независимая переменная уровня n — переменная, уникальную связь которой с зависимой переменной мы хотим установить, после контроля всех независимых переменных всех предыдущих уровней.
[3] То, что первый полюс включает таких разных школьников, не должно смущать: роль умения ждать и отношения к предмету самих по себе оценивается и учитывается в модели, и новая переменная лишь добавляет информацию о роли их соотношения.
[4] Анализ медиации — наиболее простой пример так называемого путевого анализа, группы методов, направленных на исследование прямых и косвенных эффектов ряда переменных, проверку теоретических моделей, включающих регрессионные связи.
[5] Один из примеров такой ситуации — если действуют другие медиаторы, не учтенные и не измеренные в исследовании, в частности так называемые супрессоры — переменные, подавляющие основной эффект (см. Rucker et al., 2011).
[6] Т.е. можно проверить, как изменения в независимой переменной и медиации с течением времени связаны с последующими изменениями в зависимой переменной (Little, 2013).