11.3.1. Критерий Вилкоксона — непараметрический аналог Т-критерия для парных выборок
В подпараграфе 11.1.1 мы рассматривали результаты гипотетического тренинга оптимизма. Проведем теперь анализ с помощью пакета SPSS. В файле OptimismTraining.sav содержатся результаты оценки оптимизма участников тренинга до (переменная First) и после (переменная Second) тренинга.
Нужная процедура в SPSS вызывается следующим образом: Анализ — Непараметрические критерии — Устаревшие диалоговые окна — Для двух связанных выборок (Analyze — Nonparametric Tests — Legacy Dialogs — 2 Related Tests). По умолчанию предусмотрен расчет критерия Вилкоксона (галочка в соответствующем квадратике). Окно ввода параметров анализа в данном случае устроено практически аналогично описанному выше диалоговому окну задания параметров Т-критерия Стьюдента (см. параграф 5.3). Зададим пару сравниваемых переменных Second — First (для этого в первое поле пары надо ввести имя First, а во второе Second — в отличие от Т-критерия, где порядок должен быть обратным) и нажмем кнопку ОК.
Результаты расчета критерия Вилкоксона представлены двумя таблицами: таблицей рангов разностей первой и второй выборки и собственно статистикой критерия.
| Ранги | ||||
| N | Средний ранг | Сумма рангов | ||
| Second — First | Отрицательные ранги | 2a | 2.00 | 4.00 |
| Положительные ранги | 8b | 6.38 | 51.00 | |
| Связи | 0c | |||
| Всего | 10 | |||
| a. Second < First | ||||
| b. Second > First | ||||
| c. Second = First | ||||
| Статистики критерияa | |
| Second — First | |
| Z | -2.395b |
| Асимпт. знч. (двухсторонняя) | 0.017 |
| a. Критерий знаковых рангов Уилкоксона. | |
| b. Используются отрицательные ранги. | |
Мы видим, что результаты совпадают с полученными ручным расчетом: в первой таблице приведены суммы рангов, а во второй двухсторонняя значимость. Если вы тестируете одностороннюю альтернативу, значимость надо поделить на два.
В подпараграфе 11.1.1 мы рассматривали результаты гипотетического тренинга оптимизма. Проведем теперь анализ с помощью пакета Jamovi. В файле OptimismTraining.sav содержатся результаты оценки оптимизма участников тренинга до (переменная First) и после (переменная Second) тренинга.
Расчет непараметрического критерия для сравнения парных выборок в Jamovi проводится параллельно с параметрическим t-критерием Стьюдента для парных выборок. Соответственно, для его расчета нужно зайти в меню Analysis — T-tests — Paired Samples T-test. Затем надо задать пару сравниваемых переменных аналогично описанному выше диалоговому окну задания параметров Т-критерия Стьюдента (см. параграф 5.3). Зададим пару сравниваемых переменных Second — First (для этого в первое поле пары надо ввести имя First, а во второе Second), после чего по умолчанию программа рассчитывает только t-критерий, но если в разделе Tests дополнительных настроек отметить пункт Wilcoxon rank, то в таблице статистики критериев появится и результат расчета критериев.
Резу
| Paired Samples T-Test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| First | Second | Student’s t | -3.182 | 9.000 | 0.011 | ||||||
| Wilcoxon W | 4.000 | 0.014 | |||||||||
Мы видим, что статистика критерия Вилкоксона в данном случае равна 4, а его значимость оценивается как p=0.014. Эта значимость близка к оценке различий средних с помощью t-критерия, то есть мы получаем согласованный результат с помощью двух критериев и можем достаточно уверенно сделать о различии между группами: так как в обоих случаях значимость достаточно близка к нулю, мы не можем принять нулевую гипотезу об отсутствии различий между двумя срезами. Заметим, что строго говоря, t-критерий проверяет гипотезу о равенстве средних, а Вилкоксон — о равенстве медиан, и при публикации наиболее корректно привести соответствующую выборочную статистику (а лучше обе).
В подпараграфе 11.1.1 мы рассматривали результаты гипотетического тренинга оптимизма. Проведем теперь анализ с помощью R, оценив изменение оптимизма с помощью непараметрического критерия Вилкоксона для парных выборок. В файле OptimismTraining.sav содержатся результаты оценки оптимизма участников тренинга до (переменная First) и после (переменная Second) тренинга.
Загрузив данные, сначала выведем диаграмму, отражающщую распределение интересующего нас признака (уже обсуждавшующся ранее ящичную диаграмму):
library(foreign)
data_optimism <- read.spss("OptimismTraining.sav", to.data.frame = T, reencode = "utf8")
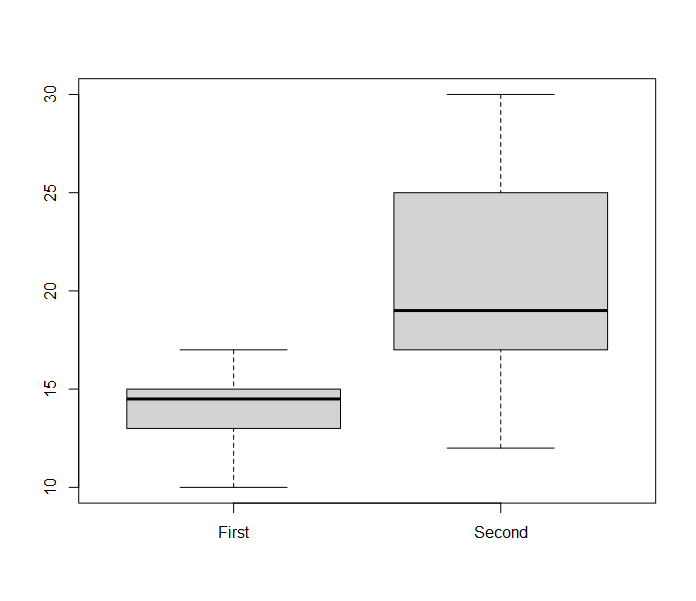
boxplot(data_optimism)boxplot(data_optimism)
Рис. 11.3.1(2)r. Распределение уровня оптимизма до и после тренинга.
Из графика видно, что уровень оптимизма в целом несколько увеличился, об этом можно судить по жирной средней линии, соответствующей медиане. Также обращает на себя внимание изменение разброса данных – после тренинга наблюдается заметное увеличение межквартильного размаха, его отражает высота «ящика». Насколько изменения медианы значимы – можно оценить с помощью критерия Вилкоксона, который в R рассчитывается с помощью функции wilcox.test. В качестве аргументов надо указать две сравниваемые выборки (в нашем случае это переменные First и Second), а также установить значение параметра paired равным TRUE, так как по умолчанию функция оценивает выборки как независимые.
wilcox.test(data_optimism$First, data_optimism$Second, paired = T) Wilcoxon signed rank exact test data: data_optimism$First and data_optimism$Second V = 4, p-value = 0.01367 alternative hypothesis: true location shift is not equal to 0
Мы видим, что статистика критерия Вилкоксона в данном случае равна 4, а его значимость оценивается как p=0.014. Результат совпадает с полученным в результате ручного расчёта в подпараграфе 11.1.1.
Рассчитаем также и t-критерий для проверки согласованности результатов непараметрического и параметрического критериев:
t.test(data_optimism$First, data_optimism$Second, paired = T) Paired t-test data: data_optimism$First and data_optimism$Second t = -3.1824, df = 9, p-value = 0.01114 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -10.607177 -1.792823 sample estimates: mean of the differences -6.2
Можно увидеть, что значимость критерии Вилкоксона близка к оценке различий средних с помощью t-критерия, то есть мы получаем согласованный результат с помощью двух критериев и можем достаточно уверенно сделать о различии между группами: так как в обоих случаях значимость достаточно близка к нулю, мы не можем принять нулевую гипотезу об отсутствии различий между двумя срезами. Заметим, что, строго говоря, t-критерий проверяет гипотезу о равенстве средних, а Вилкоксон — о равенстве медиан, и при публикации наиболее корректно привести соответствующую выборочную статистику (а лучше обе).
Критерий Вилкоксона реализован только как парный, т.е. на «вход» необходимо подать две переменные (в нашем случае результаты двух замеров). Если у вас по каким-то причинам введены разности замеров, а исходные результаты недоступны, можно выйти из положения, введя в качестве пары переменную, тождественно равную нулю. Как легко получить такую переменную, оставляем в качестве упражнения читателю.
Условия применимости критерия Вилкоксона слабее условий применимости Т-критерия — требуется, чтобы распределение разности было симметричным (подробнее см. 11.2). Если распределение разности сильно отличается от нормального, но остается симметричным, большего доверия заслуживает значимость, определенная по Вилкоксону. Чаще всего значимости, полученные двумя методами, различаются мало.
Рекомендация. Если различие велико, то наша рекомендация — постараться найти причины большого различия, проанализировав распределения каждой переменной и их разностей. Это касается всех непараметрических методов и их параметрических аналогов.
Пример 11.3.2(1). В подпараграфе 11.1.2 мы разобрали пример исследования искажений мышления у родственников шизофреников. Данные хранятся в файле Distort.sav (версия для SPSS, версия для Jamovi). Откройте его и произведите обработку методом Манна-Уитни. Первая переменная group содержит номер группы (1 — экспериментальная группа (родственники больных). 1 — контрольная группа (норма)), вторая, distort —количество ошибок.
Для расчета в SPSS надо выбрать в главном меню Анализ — Непараметрические критерии — Устаревшие диалоговые окна — Для двух независимых выборок (Analize — Nonparametric Tests — Legacy Dialogs — 2 Independent Samples). Появившееся окно устроено таким же образом, как и диалоговое окно параметров проведения Т-критерия. В поле Список проверяемых переменных (Test Variable List) следует указать сравниваемую переменную (число ошибок в нашем примере), в поле Группирующая переменная (Grouping Variable) — переменную, обозначающую принадлежность испытуемого к группе (переменная group в нашем примере). Также необходимо задать номера сравниваемых групп (1 и 2).
После нажатия кнопки ОК в окне вывода появляются результаты расчет критерия Манна-Уитни. Первая таблица содержит информацию о рангах сравниваемых переменных в двух экспериментальных группах:
| Ранги | ||||
| group | N | Средний ранг | Сумма рангов | |
| distort | 1.00 | 10 | 11.90 | 119.00 |
| 2.00 | 8 | 6.50 | 52.00 | |
| Всего | 18 | |||
Суммы рангов совпадают с рассчитанными вручную в подпараграфе 11.1.2. Как можно заметить, средний ранг в экспериментальной группе (1) больше, чем в контрольной (2)[1]. Насколько это различие значимо, можно заключить, рассмотрев следующую таблицу, содержащую результат расчета критерия Манна-Уитни.
| Статистики критерияa | |
| mistakes | |
| Статистика U Манна-Уитни | 16.000 |
| Статистика W Уилкоксона | 52.000 |
| Z | -2.132 |
| Асимпт. знч. (двухсторонняя) | 0.033 |
| Точная знч. [2*(1-сторонняя Знач.)] | 0.034b |
| a. Группирующая переменная: group | |
| b. Не скорректировано на наличие связей. | |
В первой строке статистика, рассчитанная способом, описанным в Замечании 11.1.2(2). Во второй строке всегда ставится меньшая из сумм рангов предыдущей таблицы. О том, у кого большие показатели, надо судить по средним рангам из предыдущей таблицы. Значимость можно найти в последней строке таблицы. Для не слишком больших выборок приводится точная значимость, если выборки велики, в последней строке оказывается асимптотическая значимость, а точная не рассчитывается.
Расчет критерия Манна-Уитни в Jamovi возможно в рамках сравнения двух несвязанных выборок, для этого нужно зайти в раздел Analysis — T-tests — Independent Samples T-test. Далее, в поле Dependent Variable следует указать сравниваемую переменную (число ошибок в нашем примере), в поле Grouping Variable — переменную, обозначающую принадлежность испытуемого к группе (переменная group в нашем примере).
По умолчанию в окне результатов появляется расчет t-критерия Стьюдента, а чтобы рассчитать критерий Манна-Уитни надо отметить в разделе Tests пункт Mann-Whitney U. После этого в окне вывода появляются результаты расчет критерия Манна-Уитни:
| Independent Samples T-Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| distort | Student’s t | 2.421 | 16.000 | 0.028 | |||||
| Mann-Whitney U | 16.000 | 0.034 | |||||||
Статистика U в данном рассчитана способом, описанным в Замечании 11.1.2(2).
Оценить, как именно различаются группы, можно, рассчитав описательную статистику, которая включает медиану в двух группах. Для этого в Jamovi надо отметить пункт Descriptives в разделе Additional Statistics. После этого в результатах появится таблица описательной статистики:
| Group Descriptives | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | N | Mean | Median | SD | SE | ||||||||
| distort | 1 | 10 | 18.400 | 18.500 | 5.441 | 1.720 | |||||||
| 2 | 8 | 12.500 | 12.000 | 4.721 | 1.669 | ||||||||
Как видно, медианное значение числа ошибок выше в первой, экспериментальной группе, таким образом, можно заключить, что в этой группе обнаружено значимо больше ошибок мышления.
Как и в предыдущем примере прежде, чем рассчитывать статистику критерия Манна-Уитни, после загрузки данных выведем график соотношения распределений искажений мышления в двух группах. Так как это несвязанные выборки, это можно сделать, используя формулу в качестве аргумента функции boxplot:
library(foreign)
data_distort <- read.spss("Distort.sav", to.data.frame = T, reencode = "utf8")
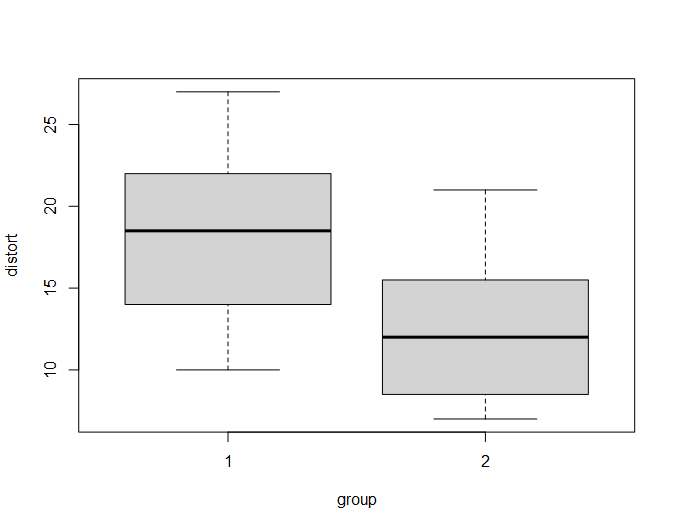
boxplot(distort ~ group, data= data_distort)
Рис. 11.3.1(2)r. Распределение числа искажений мышления в двух экспериментальных группах.
Видно, что медиана анализируемого показателя ниже во второй (контрольной) группе. Насколько значимо это различие между двумя группами можно оценить с помощью критерия Манна-Уитни, который рассчитывается в R с помощью с уже использовавшейся в предыдущем примере функции wilcox.test, но с значением аргумента paired = FALSE (это значение по умолчанию, поэтому явно его указывать необязательно).
wilcox.test(distort ~ group, data = data_distort) Wilcoxon rank sum exact test data: distort by group W = 64, p-value = 0.03428 alternative hypothesis: true location shift is not equal to 0
Статистика W в данном рассчитана способом, описанным в Замечании 11.1.2(2), причём по наибольшей сумме рангов, которая в примере равна 119 для группы 1, состоящей из 10 человек (см. пример 11.1.2). Оценка значимости при этом совпадает с симметричной оценкой по меньшей сумме рангов. Таким образом, в итоге можно сказать, что при статистике W=64 p=0.034. Как видно, медианное значение числа ошибок выше в первой, экспериментальной группе, таким образом, можно заключить, что в этой группе обнаружено значимо (при границе решения p<0.05) больше ошибок мышления.
Аналогичное сравнение средних в группах с помощью t-критерия Стьюдента дают сходный результат:
t.test(distort ~ group, data = data_distort) Welch Two Sample t-test data: distort by group t = 2.4614, df = 15.856, p-value = 0.0257 alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0 95 percent confidence interval: 0.814778 10.985222 sample estimates: mean in group 1 mean in group 2 18.4 12.5
Условия применимости Т-критерия и критерия Манна-Уитни обсуждались в подпараграфе 11.2.1. Практические рекомендации даны в конце подпараграфа 11.3.1.
11.3.3. Критерии Краскелла-Уоллиса и Джонкхиера
Упражнение 11.3.3(1). В подпараграфах 11.1.3 и 11.1.4. мы разбирали пример, описывающий исследование изменения уровня статистических знаний у студентов университета. Данные содержатся в файле StatKnowledge.sav. Обе статистики будем рассчитывать одновременно. Для этого выберем последовательность пунктов меню Анализ — Непараметрические критерии — Устаревшие диалоговые окна — Для К независимых выборок (Analize — Nonparametric Tests — Legacy Dialogs — K Independent Samples).
В отличие от дисперсионного анализа для группирующей переменной (class) здесь требуется задать диапазон изменения (от 1 до 3 в нашем случае). По умолчанию в окне задания параметров помечен квадратик H Крускала-Уоллеса (Kruskal—Wallis H). Поставьте галочку также в пункте Джонкхиера-Терпстры (Jonckheere—Terpstra). Это и есть наш критерий Джонкхиера.
Результаты расчета критерия Краскелла-Уоллиса размещаются в двух таблицах. В первой приведены суммы рангов по группам, во второй нормированная сумма квадратов отклонений от среднего ранга, имеющая распределение Хи-квадрат при условии отсутствия систематического сдвига групповых средних. Асимптотическая значимость результата приводится в последней строке второй таблицы:
| Ранги | |||
| class | N | Средний ранг | |
| Knowledge | 1.00 | 5 | 5.60 |
| 2.00 | 5 | 8.40 | |
| 3.00 | 5 | 10.00 | |
| Всего | 15 | ||
| Статистики критерияa,b | |
| Knowledge | |
| Хи-квадрат | 2.480 |
| ст.св. | 2 |
| Асимпт. знч. | 0.289 |
| a. Критерий Краскела-Уоллеса | |
| b. Группирующая переменная: class | |
Результаты расчета статистики Джонкхиера приводятся в единственной таблице:
| Критерий Джонкхиера-Терпстраa | |
| Knowledge | |
| Число уровней в class | 3 |
| N | 15 |
| Наблюденная статистика Джонкхиера-Терпстра | 52.000 |
| Среднее статистики Джонкхиера-Терпстра | 37.500 |
| Стд. отклонение статистики Джонкхиера-Терпстра | 9.465 |
| Нормир. статистика Джонкхиера-Терпстра | 1.532 |
| Асимпт. знч. (двухсторонняя) | 0.126 |
| a. Группирующая переменная: class | |
В отличие от таблицы результатов Манна-Уитни, о направлении изменения показателя надо судить по строкам Наблюденная статистика и Среднее статистики. Если первая больше второй, то групповые средние растут с возрастанием номера группы, если меньше, то, наоборот, убывают. Значимость оценивается асимптотически, поскольку распределение статистики похоже на нормальное с параметрами (мы приводим формулы для равных по объему групп)
\[ MJ=\frac{K(K-1)n^2}{4},DJ=\frac{Kn(2Kn+3)-Kn^2 (2n+3)}{72} \]
где\( n \) — объем групп, а \( K \) — их количество.
В нашем случае \( MJ=3*2*5*5/4=37.5 \), а дисперсия равна \( ((15*15)*(33)-3*(5*5)(13))/72=(7425-975)/72=89.58 \).
Стандартное отклонение получаем, извлекая из этого числа корень. Оно равно 9.465. Нормированная статистика получается делением разности наблюденного значения и среднего на стандартное отклонение, после чего по нормальному распределению вычисляется значимость.
Как мы и ожидали, на наших данных критерий Джонкхиера оказывается более мощным, чем критерий Краскелла-Уоллиса, для гипотезы о монотонном изменении знаний студентов.
Упражнение 11.3.3(1)j. В подпараграфах 11.1.3 и 11.1.4. мы разбирали пример, описывающий исследование изменения уровня статистических знаний у студентов университета. Данные содержатся в файле StatKnowledge.sav. Jamovi Позволяет рассчитать только критерий Краскелла-Уоллиса. Для этого выберем последовательность пунктов меню Analises — ANOVA — Non-Parametric — One-Way ANOVA (Kruskal-Wallis).
Для проведения анализа в данном случае надо указать группирующую переменную в окне Grouping variable (class), а в окне Dependent Variable — зависимую переменную (Knowledge).
Результаты расчета критерия Краскелла-Уоллиса размещаются в таблице:
| Kruskal-Wallis | |||||||
|---|---|---|---|---|---|---|---|
| χ² | df | p | |||||
| Knowledge | 2.480 | 2 | 0.289 | ||||
Таблица показывает, что различия между группами в данном случае незначима. Для оценки направлений этих различий (что становится важно при получении значимого результата) можно рассчитать медианы зависимой переменной в разделе Descriptives.
Упражнение 11.3.3(1)r. В подпараграфах 11.1.3 и 11.1.4. мы разбирали пример, описывающий исследование изменения уровня статистических знаний у студентов университета, учащихся на разных курсах. Данные содержатся в файле StatKnowledge.sav. Для оценки различий в уровне знаний у студентов из разных групп (т.е. курсов) рассчитаем два непараметрических критерия — Крускала-Уоллеса и Джонкхиера-Терпстры (для краткости будем далее её называть статистикой Джонкхиера). Загрузим данные, а также конвертируем группирующую переменную class, которая в исходном файле считывается как числовая, в упорядоченный фактор (это необходимо для расчёта критерия Джонкхиера):
library(foreign)
data_statKnow <- read.spss("StatKnowledge.sav", to.data.frame = T, reencode = "utf8")
data_statKnow$class <- factor(data_statKnow$class, ordered = T)
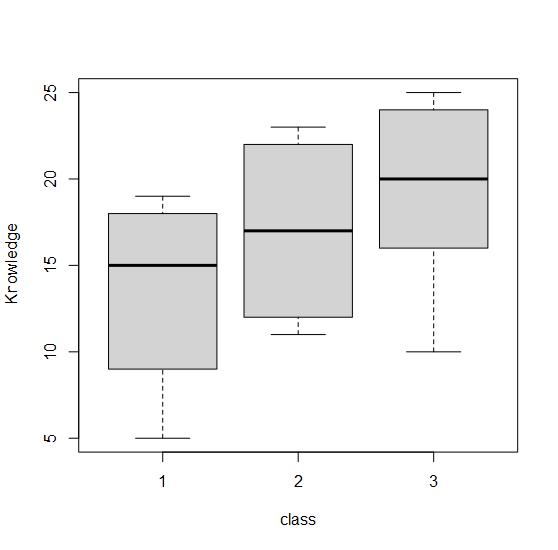
Прежде, чем рассчитывать критерии, рассмотрим график распределения уровня знаний в трех группах:
Рис. 11.3.3(2)r. Распределение уровня знаний в трех группах студентов.
Из полученного графика видно, что уровень знаний несколько увеличивается от первого ко второму и от второго к третьему курсу. То есть, в данном случае можно говорить об ожидаемом монотонном росте уровня знаний от младших куров к старшим. Однако, насколько это значимый рост из рисунка неочевидно, проверим гипотезу о неравенстве медиан уровня знаний в трех курсах с помощью критерия Крускалла-Уоллиса. В R это можно сделать с помощью функции kruskal.test, указав как аргументы формулу соотношения зависимой и независимой переменной и имя таблицы анализируемых данных:
kruskal.test(Knowledge ~ class, data = data_statKnow) Kruskal-Wallis rank sum test data: Knowledge by class Kruskal-Wallis chi-squared = 2.48, df = 2, p-value = 0.2894
Статистика критерия Краскелла-Уоллиса представляет собой нормированную сумму квадратов отклонений от среднего ранга, имеющая распределение Хи-квадрат при условии отсутствия систематического сдвига групповых средних. Асимптотическая значимость этого результата приводится в конце. Как видно, в данном случае результат таков: χ2(2) = 2.48, p = 0.289. Значимость достаточно далека от нуля, что не позволяет нам отклонить гипотезу о равенстве медиан зависимой переменной в трех сравниваемых группах.
Попробуем рассчитать статистику Джонкхиера. В R она не входит в базовый набор тестов и её расчет требует подключения дополнительных пакетов (существует несколько вариантов), мы воспользуемся одним из них – DescTools. В нем есть функция JonckheereTerpstraTest, которая рассчитывает нужный нам критерий, формат аргументов – аналогичен используемому выше:
library(DescTools) JonckheereTerpstraTest(Knowledge ~ class, data = data_statKnow) Jonckheere-Terpstra test data: Knowledge by class JT = 52, p-value = 0.1416 alternative hypothesis: two.sided
Как мы видели из рисунка Рис. 11.3.3(2)r, уровень знаний от младшего к старшим курсам растёт. В силу этого, как мы и ожидали, на наших данных критерий Джонкхиера оказывается более мощным, чем критерий Краскелла-Уоллиса, для гипотезы о монотонном изменении знаний студентов.
Ещё более «сильный» с точки зрения оценки значимости результат мы можем получить, если будем проверять направленную гипотезу о возрастании уровня знания. По умолчанию функция JonckheereTerpstraTestоценивает двухстороннюю гипотезу, которая допускает как монотонное возрастание, так и убывание зависимой переменной. Если мы, исходя из содержательных соображений, уверены в том, что изменения в уровне студентов при обучении могут быть только положительными, то мы можем проверять направленную гипотезу. В этом случае аргументами функции нужно указать сначала зависимую переменную, затем независимую (группирующую), а затем – параметр , alternative = «increasing»:
JonckheereTerpstraTest(data_statKnow$Knowledge, data_statKnow$class, alternative = "increasing") Jonckheere-Terpstra test data: data_statKnow$Knowledge and data_statKnow$class JT = 52, p-value = 0.07079 alternative hypothesis: increasing.
Как мы видим, в этом случае значимость критерия уменьшается в 2 раза и становится ближе к нулю.
11.3.4. Коэффициент корреляции Спирмена
Упражнение 11.3.4(1). Как мы разъясняли в подпараграфа 11.3.2, непараметрические критерии работают на порядковых шкалах, в отличие от параметрических, которые требуют интервальности шкал. С этим связано их преимущество в ситуациях, когда мы сталкиваемся с выбросами, т.е. значениями показателя, аномально отличающимися от среднего по генеральной совокупности значения. Мы разберем сейчас пример, когда выброс меняет результат исследования кардинально. Предположим, школьникам предложили выполнить сразу два задания ЕГЭ в ограниченное время. В файле CorrelationPS.sav (версия для SPSS, версия для Jamovi) даны результаты. Переменная RL представляет оценку по русскому языку, а GG — по географии. Один из учеников почти все время потратил на sms-переписку, поэтому показал плохой результат по обоим предметам, однако его истинное занятие не было замечено преподавателем.
Рассчитайте коэффициенты корреляции Пирсона и Спирмена и сравните их.
Напомним, что для этого в SPSS надо выбрать пункты меню Анализ — Корреляции — Парные (Analyze — Correlation — Bivariate). Чтобы рассчитать обе корреляции, отметьте галочкой квадраты, подписанные Пирсон (Pearson) и Спирман (Spearman). В Jamovi, аналогично, надо вызвать анализ корреляций в меню Analyses — Regression — Correlation Matrix. Для добавления к корреляции Пирсона расчет коэффициента Спирмена надо выбрать пункт Spearman в разделе Correlation Coefficients. В R можно использовать любую из рассмотренных ранее функций – cor, cor.test из базового набора или corr.test из пакета psych (см. пример 9.3(3)r) , указав дополнительный аргумент method = «spearman».
В результате получаем корреляции разных знаков — положительную по Пирсону и отрицательную по Спирмену. В данном случае у нас нет оснований удалить выброс, однако его влияние корреляция по Спирмену минимизирует.
Упражнение 11.3.4(2). Постройте график рассеяния и скажите, в каких пределах можно изменять данные последнего испытуемого, чтобы корреляция по Спирмену не менялась. Сделайте какие-то из этих изменений и посмотрите, как ведет себя корреляция по Пирсону.
Упражнение 11.3.5(1)s. Проведем расчеты подпараграфа 11.1.6 о решении творческих задач. Откройте файл PolyakovExp.sav. Переменная Diagnosis кодирует принадлежность группе больных или здоровых, переменная TaskSolving содержит информацию о решении задачи.
Для того чтобы построить таблицы сопряженности и рассчитать критерий Хи-квадрат Пирсона, выберем пункт меню Анализ — Описательные статистики — Таблицы сопряженности (Analysis — Descriptive statistics — Crosstabs). В появившемся окне одну из переменных нужно указать в поле Строки (Rows), другую — в поле Столбцы (Columns). Для того чтобы ориентация таблицы совпадала с приведенной в предыдущем параграфе, перенесите переменную Diagnosis в окно Строки, вторую переменную — в Столбцы. Для того чтобы рассчитать ожидаемые частоты, нажмите на кнопку Ячейки (Cells) справа и поставьте галочку на Ожидаемые частоты (Expected Frequencies). Чтобы рассчитать Хи-квадрат Пирсона нажмите на кнопку Статистики (Statistics) справа и поставьте галочку в клетке Хи-квадрат (Chi—square). Обратите внимание, что, если этот пункт не выбран, в выводе не будет оцениваться значимость.
Первая таблица результатов — «Сводка обработки наблюдений» — содержит вспомогательную информацию о количестве испытуемых и пропущенных результатов. Вторая таблица приведена ниже:
| Таблица сопряженности Контрольная группа / шизофрения * Решение задачи | |||||
| Решение задачи | Итого | ||||
| Не решил | Решил | ||||
| Контрольная группа / шизофрения | Норма | Частота | 30 | 25 | 55 |
| Ожидаемая частота | 22.0 | 33.0 | 55,0 | ||
| Шизофрения | Частота | 10 | 35 | 45 | |
| Ожидаемая частота | 18.0 | 27.0 | 45.0 | ||
| Итого | Частота | 40 | 60 | 100 | |
| Ожидаемая частота | 40.0 | 60.0 | 100.0 | ||
Она повторяет нашу таблицы наблюдаемых и ожидаемых частот подпараграфа 11.1.6. Наконец, третья таблица предоставляет нам оценки значимости результата.
| Критерии хи-квадрат | |||||
| Значение | ст.св. | Асимпт. значимость (2-стор.) | Точная значимость (2-стор.) | Точная значимость (1-стор.) | |
| Хи-квадрат Пирсона | 10.774a | 1 | 0.001 | ||
| Поправка на непрерывностьb | 9.470 | 1 | 0.002 | ||
| Отношение правдоподобия | 11.138 | 1 | 0.001 | ||
| Точный критерий Фишера | 0.001 | 0.001 | |||
| Линейно-линейная связь | 10.667 | 1 | 0.001 | ||
| Кол-во валидных наблюдений | 100 | ||||
| a. В 0 (0,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 18,00. | |||||
| b. Вычисляется только для таблицы 2×2. | |||||
Для небольших выборок рассчитывается точная значимость результата по соответствующему (так называемому гипергеометрическому) распределению. В данном случае это двухсторонняя значимость 0.001. Вверху слева значение статистики Хи-квадрат, отличающееся от полученного нами ошибкой округления. Однако значимость по критерию Хи-квадрат (если выборка велика и нет точной значимости) надо брать из второй строки, где вводится необходимая для таблиц только размера 2×2 поправка.
Значимость близка к нулю, гипотеза исследования довольно надежно подтверждается.
Упражнение 11.3.5(2)s. Проведем расчеты примера 11.1.7(1) о стрессе сотрудников банка. Данные записаны в файл BankStress.sav. Переменная Period кодирует начало, середину и конец недели, переменная StressGroup кодирует уровень стресса. Расставьте самостоятельно переменные в соответствующих полях в окне задания таблицы сопряженности так, чтобы ориентация таблицы совпадала с таблицами из примера 11.1.7(1). Поставьте также необходимые знаки, чтобы получить ожидаемые значения и статистику.
Таблица вывода, касающаяся значимости, в данном случае проще, чем в предыдущем: нужная нам значимость проставлена в первой строке, альтернатив нет.
Упражнение 11.3.5(3)s. На самом деле данные о стрессе получены первоначально в виде показателя, изменяющегося от 1 до 60 (переменная StressScore в том же файле BankStress.sav). Переменная StressGroup представляет собой некоторое «огрубление» балла. Разберитесь, как именно перекодированы данные StressScore в StressGroup.
Технически такую перекодировку можно выполнить только почти вручную. Мы предложим вам сделать похожую, но требующую минимум усилий перекодировку. Выберите пункты меню Преобразовать — Ранжировать (Transform — Rank cases). В полученном окне переведите в поле Переменные (Variables) имя StressScore, а затем нажмите кнопку Типы рангов (Rank types). В полученном окне выберите N-разбиение (Ntiles) на 3 группы. Другие галочки можно убрать. В результате получается переменная NStressS, в которой кодируется, к какой из третей выборки принадлежит результат данного испытуемого.
Проделайте анализ с помощью таблицы сопряженности и сопоставьте результаты с предыдущим анализом.
Упражнение 11.3.5(4). Проведите дисперсионный анализ с зависимой переменной StressScore и фактором Period. Сравните результаты. Корректен ли такой вид анализа для таких данных?
Упражнение 11.3.5(1)j. Проведем расчеты подпараграфа 11.1.6 о решении творческих задач. Откройте файл PolyakovExp.sav. Переменная Diagnosis кодирует принадлежность группе больных или здоровых, переменная TaskSolving содержит информацию о решении задачи.
Для того чтобы построить таблицы сопряженности и рассчитать критерий Хи-квадрат Пирсона, выберем пункт меню Frequencies – Independent Samples ( test of association) В появившемся окне одну из переменных нужно указать в поле Rows, другую — в поле Columns. В принципе, не важно, какая переменная будет отображаться по строкам, а какая — по столбцам, но для того, чтобы ориентация таблицы совпадала с приведенной в предыдущем параграфе, перенесите переменную Diagnosis в окно Rows, вторую переменную — в Columns. Для того чтобы рассчитать ожидаемые частоты, откройте раздел Cells и поставьте галочку на Expected counts. Если размерность вашей таблицы 2*2, то в подменю Statistics надо поставить галочку на continuity correction.
В окне результатов вы увидите две таблицы. Первая:
| Contingency Tables | |||||||||
| TaskSolving | |||||||||
| Diagnosis | Не решил | Решил | Total | ||||||
| Норма | Observed | 30 | 25 | 55 | |||||
| Expected | 22.0 | 33.0 | 55.0 | ||||||
| Шизофрения | Observed | 10 | 35 | 45 | |||||
| Expected | 18.0 | 27.0 | 45.0 | ||||||
| Total | Observed | 40 | 60 | 100 | |||||
| Expected | 40.0 | 60.0 | 100.0 | ||||||
Она повторяет нашу таблицы наблюдаемых и ожидаемых частот подпараграфа 11.1.6. Вторая таблица предоставляет нам оценки значимости результата.
| χ² Tests | |||||||
| Value | df | p | |||||
| χ² | 10.8 | 1 | 0.001 | ||||
| χ² continuity correction | 9.47 | 1 | 0.002 | ||||
| N | 100 | ||||||
Для небольших выборок рассчитывается точная значимость результата по соответствующему (так называемому гипергеометрическому) распределению. В данном случае это двухсторонняя значимость 0.001. Вверху слева значение статистики Хи-квадрат, отличающееся от полученного нами ошибкой округления. Однако значимость по критерию Хи-квадрат (если выборка велика и нет точной значимости) надо брать из второй строки, где вводится необходимая только для таблиц размера 2×2 поправка.
Значимость близка к нулю, гипотеза исследования довольно надежно подтверждается.
Упражнение 11.3.5(2)j. Проведем расчеты примера 11.1.7(1) о стрессе сотрудников банка. Данные записаны в файл BankStress.sav. Переменная Period кодирует начало, середину и конец недели, переменная StressGroup кодирует уровень стресса. Расставьте самостоятельно переменные в соответствующих полях в окне задания таблицы сопряженности так, чтобы ориентация таблицы совпадала с таблицами из примера 11.1.7(1). Поставьте также необходимые знаки, чтобы получить ожидаемые значения и статистику.
Таблица вывода, касающаяся значимости, в данном случае проще, чем в предыдущем: таблица имеет размерность 3*3 и поправку вводить не надо.
Упражнение 11.3.5(3)j. На самом деле данные о стрессе получены первоначально в виде показателя, изменяющегося от 1 до 60 (переменная StressScore в том же файле BankStress.sav). Переменная StressGroup представляет собой некоторое «огрубление» балла. Разберитесь, как именно перекодированы данные StressScore в StressGroup.
Технически такую перекодировку можно выполнить только почти вручную. Мы предложим вам сделать похожую, но требующую минимум усилий перекодировку. Выберите переменную StressScore и во вкладке Data нажмите пункт меню Transform. В полученном окне в подменю using transform выберите Create New Transform и, добавляя условия перекодирования (add recode condition), введите необходимые условия. Не забудьте выставить правильный тип шкалы в выпадающем списке Measure type.
Проделайте анализ с помощью таблицы сопряженности и сопоставьте результаты с предыдущим анализом (он должен быть идентичным).
Упражнение 11.3.5(4)j. Проведите дисперсионный анализ с зависимой переменной StressScore и фактором Period. Сравните результаты. Корректен ли такой вид анализа для таких данных?
Упражнение 11.3.5(1)s. Проведем расчеты подпараграфа 11.1.6 о решении творческих задач. Откройте файл PolyakovExp.sav. Переменная Diagnosis кодирует принадлежность группе больных или здоровых, переменная TaskSolving содержит информацию о решении задачи.
Для того чтобы построить таблицы сопряженности в R есть много различных инструментов, мы предлагаем читателю использовать один из наиболее удобных – это функция crosstabиз пакета descr . У этой функции много различных параметров, которые можно изучить в описании, здесь мы остановимся на наиболее важных для нас. Минимально, для получения таблицы нужно указать две переменные, одну – в аргументе dep (от dependent, она будет выведена в таблице по строкам), а вторую – в аргументе indep (от independent, она будет выведена по столбцам). Также в качестве дополнительных параметров можно установить значение параметра expected = TRUE (для отображения ожидаемых частот), а для расчета статистики Хи-квадрат Пирсона также нужно установить значение параметра chisq = TRUE:
library(foreign)
library(descr)
data_PolyakovExp <- read.spss("PolyakovExp.sav", to.data.frame = T, reencode = "utf8")crosstab(dep = data_PolyakovExp$TaskSolving, indep = data_PolyakovExp$Diagnosis, expected = TRUE, chisq = TRUE)
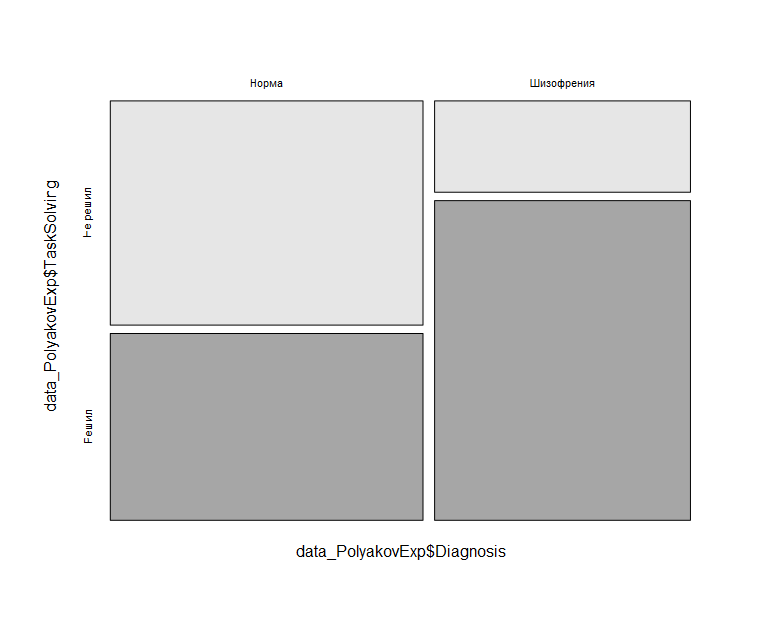
В результате функция выводит таблиу сопряженности, значение критерия хи-квадрат Пирсона и графическое отображение результата:
Cell Contents |-------------------------| | Count | | Expected Values | |-------------------------| ========================================================== data_PolyakovExp$Diagnosis data_PolyakovExp$TaskSolving Норма Шизофрения Total ---------------------------------------------------------- Не решил 30 10 40 22 18 ---------------------------------------------------------- Решил 25 35 60 33 27 ---------------------------------------------------------- Total 55 45 100 ========================================================== Statistics for All Table Factors Pearson's Chi-squared test ------------------------------------------------------------ Chi^2 = 10.77441 d.f. = 1 p = 0.00103 Pearson's Chi-squared test with Yates' continuity correction ------------------------------------------------------------ Chi^2 = 9.469697 d.f. = 1 p = 0.00209 Minimum expected frequency: 18
Как можно заметить, таблица сопряженности с точностью до поворота повторяет нашу таблицы наблюдаемых и ожидаемых частот подпараграфа 11.1.6. Графическое отображение может быть удобно для лучшего понимая результата – на ней достаточно хорошо видно, что среди больных шизофренией доля решивших задачу заметно больше, чем в группе контрольной группе.
Для небольших выборок рассчитывается точная значимость результата по соответствующему (так называемому гипергеометрическому) распределению, которая содержится в строке Pearson’s Chi-squared test. В данном случае это двухсторонняя значимость 0.001. Значение этой статистики Хи-квадрат совпадает с полученным при ручном расчете с точностью до округления. Однако при увеличении выборки в случае таблиц 2×2 более точно значимость оценивается по критерию Хи-квадрат с поправкой на непрерывность (строка Pearson’s Chi-squared test with Yates’ continuity correction).
Значимость близка к нулю, гипотеза исследования довольно надежно подтверждается.
Упражнение 11.3.5(2)s. Проведем расчеты примера 11.1.7(1) о стрессе сотрудников банка. Данные записаны в файл BankStress.sav. Переменная Period кодирует начало, середину и конец недели, переменная StressGroup кодирует уровень стресса. Распределите самостоятельно переменные в аргументы функции crosstab (не забудьте загрузить пакет descry при необходимости) так, чтобы ориентация таблицы совпадала с таблицами из примера 11.1.7(1). Укажите также дополнительные параметры, чтобы получить ожидаемые значения и статистику.
Упражнение 11.3.5(3)s. На самом деле данные о стрессе получены первоначально в виде показателя, изменяющегося от 1 до 60 (переменная StressScore в том же файле BankStress.sav). Переменная StressGroup представляет собой некоторое «огрубление» балла. Разберитесь, как именно перекодированы данные StressScore в StressGroup.
Решим задачу разделения выборки на три равные части по параметру StressScore.Технически такую перекодировку можно выполнить в R можно провести различными способами. Мы прилагаем сделать это с помощью функции ntileиз пакета dplyr. При этом предлагаем сразу конвертировать полученную переменную в упорядоченный фактор:
library(dplyr) data_BankStress$StressGroup_3 <- factor(ntile(data_BankStress$StressGroup, 3), ordered = T)
В результате в таблицу добавляется переменная StressGroup_3, в которой кодируется, к какой из третей выборки принадлежит результат данного испытуемого.
Проделайте анализ с помощью таблицы сопряженности и сопоставьте результаты с предыдущим анализом.
Упражнение 11.3.5(4). Проведите дисперсионный анализ с зависимой переменной StressScore и фактором Period. Сравните результаты. Корректен ли такой вид анализа для таких данных?
Заключительное упражнение 11.3.5(5). Это последнее упражнение нашего учебника можно считать итоговым тестом. Откройте файл LastExersize.sav. Данные описывают динамику результативности юных спортсменов, тренирующихся в школе, ориентированной на высокие спортивные достижения и практикующей очень жесткий режим поощрений и наказаний, однако без отчисления за плохие показатели. Переменная Year кодирует год тренировки (оценивались разные учащиеся первого, второго и третьего года тренировок, по 60 человек каждого года). Переменная Results кодирует отнесенные к возрастным нормам спортивные результаты учеников, т.е. рост результатов означает прогресс более быстрый, чем средний прогресс в спортивных школах данного профиля.
Нарисуйте график рассеяния, примените уместные известные вам методы и опишите результаты. После завершения самостоятельной работы наше описание вы можете найти в файле LastExersizeDescription.pdf.
>> следующий параграф>>
[1] Обратите внимание, что сумма рангов зависит от количества испытуемых в группах. Если в группах разное количество испытуемых, делать содержательные выводы о различии между группами по этому показателю нельзя и следует анализировать показатель «средний ранг».