9.1.1. Коэффициент корреляции Пирсона
Задача о связи характеристик изучаемого предмета — одна из наиболее часто встречающихся в психологических исследованиях.
Типичная задача такого рода возникает в исследованиях, где каждый испытуемый характеризуется двумя или бóльшим числом показателей. Пусть, например, 70 детей разного возраста решают задачи некоторого теста на запоминание несложного вербального материала. Результат оценивается в процентах воспроизведенного материала. Каждый испытуемый характеризуется парой чисел — возрастом и оценкой успешности воспроизведения материала, которые позволяют отобразить его характеристики на диаграмме рассеяния (рис. 9.1.1(1)), которая получается следующим образом. На плоскости в системе координат «возраст» (горизонтальная ось) — «успешность воспроизведения» (вертикальная ось) каждый испытуемый отображается точкой, координаты которой — это его показатели по указанным переменным.
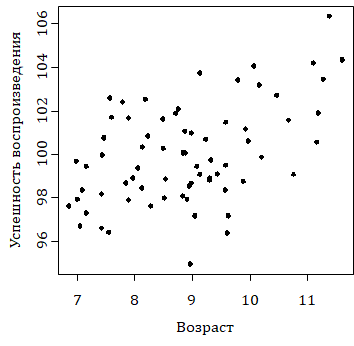
Рис. 9.1.1(1). Диаграмма рассеяния. По оси абсцисс отложен возраст испытуемого, по оси ординат — оценки по тесту
Мы видим по диаграмме, что имеется тенденция повышения результата тестирования при увеличении возраста испытуемого.
Другой пример: те же 70 испытуемых взвешены на весах. Диаграмма для этого показателя и возраста выглядит так:
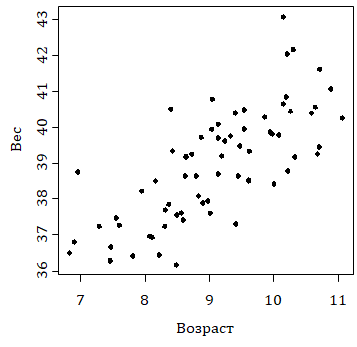Рис. 9.1.1(2). Диаграмма рассеяния. По оси абсцисс отложен возраст испытуемого, по оси ординат — вес
На этой диаграмме наблюдается естественная тенденция увеличения веса при увеличении возраста испытуемого, однако мы видим различие в степени выраженности этих тенденций на двух диаграммах. Показатели, к изучению которых мы теперь переходим, предназначены для оценивания именно этой степени выраженности. В данной главе мы будем предполагать, что все переменные измерены в интервальной шкале. Поскольку речь идет о связи переменных, то показатель этой связи не должен зависеть от единиц, в которых мы измеряем, например, вес: связь веса и возраста должна быть описана независимо от того, измеряется ли вес в килограммах или фунтах. Таким инвариантным показателем связи является коэффициент корреляции Пирсона.
Вычислим сначала выборочные оценки \( \overline{x}, s_x, \overline{y},s_y \) по уже знакомым нам формулам \( \overline{x}=\frac{1}{n}(x_1+x_2+\dots+x_n \)) и \( s_x=\sqrt{\frac{1}{n-1}((x_1-\overline{x})^2+(x_2-\overline{x})^2+\dots+(x_n-\overline{x})^2)} \) (и аналогично для y).
Коэффициент корреляции Пирсона вычисляется по формуле
\[ r_{xy}=\frac{\frac{1}{n-1}((x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+\dots+(x_n-\overline{x})(y_n-\overline{y})}{s_xs_y} \]
Формулу можно преобразовать:
\[ r_{xy}=\frac{1}{n-1}(\frac{(x_1-\overline{x})}{s_x}\cdot\frac{(y_1-\overline{y})}{s_y}+\dots+\frac{(x_n-\overline{x})}{s_x}\cdot\frac{(y_n-\overline{y})}{s_y}) \]
Если обозначить \( x^{‘}_i=\frac{x_i-\overline{x}}{s_x} \), \( y^{‘}_i=\frac{y_i-\overline{y}}{s_y} \) (стандартизованные переменные), то формула корреляции принимает простой вид
\[ r_{xy}=\frac{1}{n-1}(x^{‘}_1y^{‘}_1+x^{‘}_2y^{‘}_2+\dots+x^{‘}_ny^{‘}_n) \]
На рис. 9.1.1(3) показаны диаграммы, соответствующие различным значениям коэффициента корреляции. При изменении единиц измерения коэффициент Пирсона не меняется, поэтому мы не указывали единицы измерения на осях.
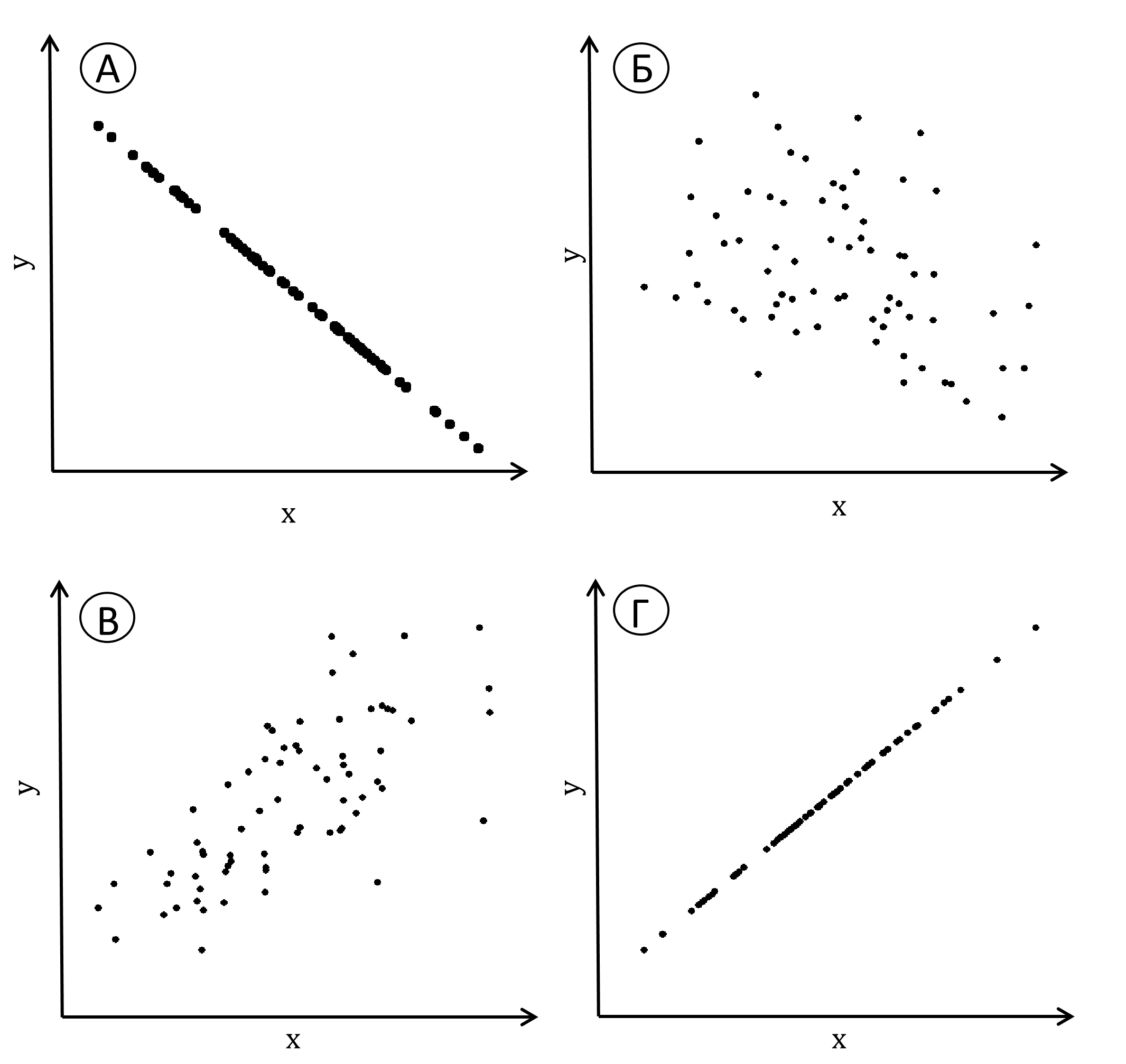Рис. 9.1.1(3). Диаграммы рассеяния при некоторых значениях коэффициента корреляции Пирсона: а) r=−1; б) r=−0.35; в) r=0.7; г) r=1
Самая большая положительная корреляция, равная единице, соответствует линейной связи с положительным коэффициентом при \( y_i=a\cdot x_y+b \) при \( a>0 \) (это не значит, что y зависимая переменная, а x независимая; для корреляции переменные совершенно равноправны; корреляция сама по себе вообще ничего не говорит о причинно-следственных связях между переменными — см. 9.1.6 ). На другом полюсе — равная минус единице корреляция для линейно связанных выборочных значений с отрицательным коэффициентом: \( y_i=a\cdot x_y+b \) при \( a<0 \). Коэффициент корреляции не может превышать единицу и быть меньше минус единицы. При наличии линейной связи он равен по модулю единице при любых значениях a и b. Если сопоставляемые переменные на самом деле независимы, то выборочный коэффициент корреляции будет приблизительно равен нулю, а облако точек на диаграмме рассеяния будет более или менее округлым или вытянутым вдоль одной или другой оси.
Если в первом примере вместо процента запомненных стимулов характеризовать испытуемых количеством не запомненных, то новая переменная будет связана с исходной соотношением «процент не запомненных стимулов» = 100 — «процент запомненных стимулов». Это допустимое для интервальных шкал преобразование меняет знак коэффициента корреляции, сохраняя его модуль.
Коэффициент корреляции Пирсона измеряет так называемую линейную связь переменных, которая на графиках выражается вытянутостью облака точек на диаграмме рассеяния вдоль не параллельной осям прямой линии. Для изображенных на рис. 9.1.1(4) конфигураций коэффициент корреляции Пирсона будет близким к нулю, несмотря на очевидность связи переменных.
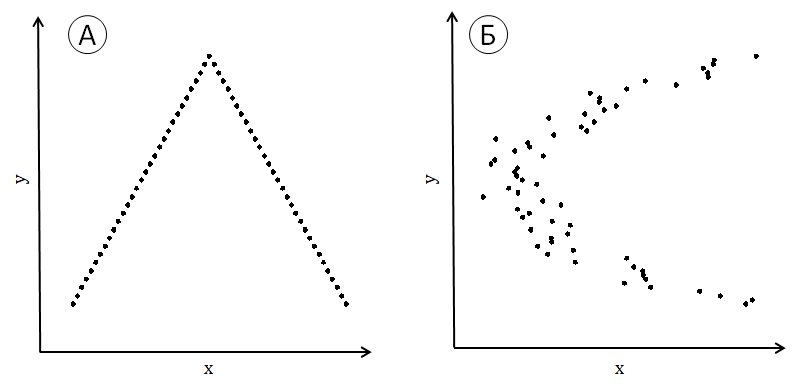Рис. 9.1.1(4). Примеры пар выборок с очевидной связью значений, но близкой к нулю корреляцией
Числитель формулы корреляции Пирсона иногда представляет отдельный интерес и имеет собственное название — коэффициент ковариации:
\[ r_{xy}=\frac{1}{n-1}((x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+\dots+(x_n-\overline{x})(y_n-\overline{y})) \]
При изменении единиц измерения он, в отличие от коэффициента корреляции, изменяется пропорционально выборочным значениям. Соответственно последним, коэффициент ковариации может принимать значения от минус до плюс бесконечности.
9.1.2. Проверка статистических гипотез о связи переменных
Выборочный коэффициент корреляции оценивает подразумеваемую исследователем реальную связь между переменными. Как и в случае оценки среднего значения, нас интересуют два вопроса: (1) Насколько сильна связь между переменными; (2) Насколько надежна наша оценка. Сила связи между переменными по всей генеральной совокупности существует объективно. Если ее измерять корреляцией, то она будет выражаться числом от −1 до 1. Выборочная корреляция этих переменных будет колебаться вокруг истинного показателя силы связи. Трудность состоит в том, что, получив выборочную корреляцию, мы не можем знать, ни насколько она отклоняется от истинного значения, ни даже в какую сторону. В случае корреляции оценка обычно выражается в терминах значимости.
Проделаем небольшое упражнение.
Упражнение 9.1.2(1). Возьмите две симметричные монеты достоинством в один рубль и один евро. Проведите серию четырех подбрасываний пары монет и запишите результаты в виде \( (x_1, y_1),\dots,(x_4, y_4) \) , полагая
\( x_i=0 \), если рубль выпал цифрой;
\( x_i=1 \), если рубль выпал гербом;
\( y_i=0 \), если евро выпал цифрой;
\( y_i=1 \), если евро выпал гербом.
Подсчитайте коэффициент корреляции Пирсона. Истинная корреляция между результатами двух монет равна, разумеется, нулю. Повторите процедуру несколько раз и убедитесь, что нулевое значение выборочного коэффициента корреляции выпадает примерно один раз из трех. При многократном повторении опыта можно убедиться, что его результат имеет некоторое распределение, симметричное относительно нуля. Это распределение зависит от объема выборки n: чем больше n, тем меньше дисперсия распределения, тем ближе к нулю ее вероятные значения.
В таблице 9.1.2(2) приведены двухсторонние квантили распределения выборочного коэффициента корреляции по Пирсону для \( n=10 \). Они рассчитаны для выборок, полученных испытаниями двух нормально распределенных случайных величин, теоретическая корреляция между которыми равна нулю. Дихотомический результат подбрасывания монеты не распределен нормально, однако некоторое представление о возможных результатах наших испытаний табличный квантиль все же дает.
Таблица 9.1.2(2) Двусторонние квантили распределения коэффициента Пирсона для n = 10
| \( \alpha \) | 0.05 | 0.025 | 0.01 | 0.005 |
| \( r_\alpha(10) \) | 0.497 | 0.576 | 0.658 | 0.709 |
Обычно при исследовании связи переменных статистической гипотезой \( H_0 \) будет гипотеза об отсутствии связи, т.е. о независимости переменных. Альтернативная гипотеза \( H_1 \) (т.е. гипотеза, к которой мы склоняемся, получив большие по модулю значения выборочной корреляции) будет утверждать только наличие связи [1]. Можно оценить значимость относительно данного результата (полученной парной выборки) гипотез о других значениях теоретической корреляции, но это требует некоторых дополнительных усилий (см. подпараграф 9.2.3). Если истинна гипотеза \( H_0 \), то выборочный коэффициент корреляции будет принимать значения, более или менее близкие к нулю. Если выборочная корреляция принимает достаточно большое по модулю значение, которому соответствует значимость, измеряемая маленьким числом, то мы склоняемся к гипотезе \( H_1 \) о наличии связи, но без указания точного значения теоретической корреляции.
Можно заметить, что если верна гипотеза об отсутствии зависимости между случайными величинами, то выборочный коэффициент при \( n=10 \) может принимать тем не менее довольно большие значения, так что уровень значимости 0.05 для принятия гипотезы о зависимости случайных величин требует, чтобы выборочный коэффициент корреляции достигал почти 0.5 (см. 9.1.2(2)). В связи с этим надо иметь в виду, что даже выборочная корреляция, например 0.6, вполне может согласовываться с истинной корреляцией, равной 0.2 [2].
9.1.3. Простая линейная регрессия
Применение линейного регрессионного анализа имеет специфические черты по сравнению с другими методами обработки данных. Его непосредственное употребление ограничено, в основном, задачами о предсказании значений зависимой переменной по известным значениям аргумента (или аргументов), что в психологии задача не слишком востребованная. Однако, во-первых, линейная регрессия входит как часть во многие другие методы (например, анализ медиации и модерации, о которых речь пойдет в следующей главе), и, во-вторых, служит простым примером отыскания наилучших параметров для модели определенного типа, и психологу полезно понимать суть этого метода. Качество каждого набора параметров, а затем и модели в целом, оценивается процентом дисперсии, который остался вне предсказаний, сделанных моделью по данным значениям аргументов. Замечательным результатом для читателя будет здесь улавливание аналогий с двухфакторным дисперсионным анализом.
9.1.4. Определение регрессионной прямой
Простая линейная регрессия имеет дело с данными того же типа, что и корреляция, но придает им несколько иной смысл. Вот пример: в эксперименте шестилетнего ребенка оставляли на 15 минут одного в комнате перед вкусной шоколадной конфетой, пообещав дать две, если эту конфету он не тронет. Через два года оценивалась его успеваемость в школе. Оказалось, что время, в течение которого ребенок удерживался от соблазна, предсказывает его успеваемость во втором классе с точностью 60%. Уточним, что стоит за этим числом.
Пусть в результате эксперимента с участием n детей получены n пар чисел
\[ (x_1,y_1),(x_2,y_2),\dots,(x_n,y_n) \]
Линейный регрессионный анализ исходит из гипотезы, что интегральный показатель успеваемости данного ребенка представляет собой сумму детерминированного вклада линейной функции от «времени терпения» и случайного вклада, зависящего от его неучтенных индивидуальных особенностей.
Таким образом, предполагается зависимость \( y_i=ax_i+b+\alpha_i \), где a и b некоторые коэффициенты, а \( \alpha_i \) случайная добавка (она называется «остаток»), для каждого испытуемого своя. Ясно, что задача не имеет очевидного однозначного решения. Всякая прямая может фигурировать в правой части равенства, от ее выбора будет зависеть только совокупность компенсирующих «остатков» \( \alpha_i \). «Лучшей» из этих прямых будем считать ту прямую, для которой эта совокупность в каком-то смысле минимальна, т.е. ту, которая «ближе» к точкам, представляющим испытуемых. С точки зрения математики это «ближе» разумнее всего понимать так: надо найти такую прямую, чтобы сумма квадратов «остатков» \( \alpha^2_1+\alpha^2_2+\dots+\alpha^2_i \) была минимальна [3].
Каждую пару чисел из \( (x_i,y_i) \) можно рассматривать как точку на плоскости в системе координат \( (x,y) \).
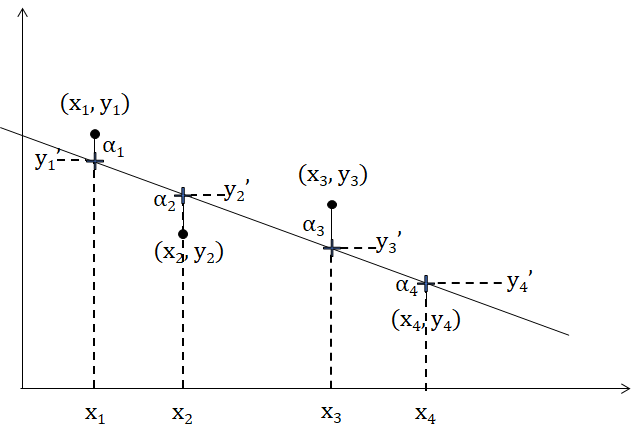Рис.9.1.4(1). Выборочные значения, регрессионная прямая и ошибки регрессионной модели.
На рис. 9.1.4(1) изображены четыре точки, отображающие выборку \( (x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4) \), и регрессионная прямая с уравнением \( y=ax+b \). Крестиками отмечены на прямой точки, которые имеют предсказанные регрессионным уравнением ординаты (т.е. ординаты \( y^{‘}_1=ax_1+b,y^{‘}_2=ax_2+b,y^{‘}_3=ax_3+b,y^{‘}_4=ax_4+b \) соответственно). Вертикальное расстояние\( y_i-y^{‘}_i \) от точки выборки, до точки, помеченной крестиком, и есть \( \alpha_i \) — ошибка данной модели для данной точки. Сумма квадратов ошибок и будет характеризовать качество данной прямой как модели для данной выборки.
Операция по нахождению наилучшей в этом смысле прямой, описывающей подобную зависимость, называется линейным регрессионным анализом, а метод, обеспечивающий решение, которое характеризуется минимумом дисперсии случайной составляющей, называется методом наименьших квадратов (Гаусса).
Наилучшая в указанном смысле прямая всегда проходит через точку \( (\overline{x}, \overline{y}) \) и имеет угловой коэффициент и свободный член, соответственно
\[ a=\frac{r_{xy}\cdot s_y}{s_x}, b=\overline{y}-\overline{x}\cdot a, \]
где \( r_{xy} \) — коэффициент корреляции. Т.е. наилучшей в смысле минимума суммы квадратов отклонений является прямая
\[ y=a⋅x+\overline{y}-\overline{x}\cdot a. \]
Прикладной смысл регрессионной прямой заключается в том, что ордината точки на прямой над данным значением аргумента x и есть предсказание успеваемости для ребенка, показавшего x минут терпения. Что означает 60% точности, мы разъясним по рис. 9.1.4(1).
Общая дисперсия результатов детей есть дисперсия выборки \( (y_1,\dots,y_4) \). Дисперсия предсказанных результатов есть дисперсия выборки \( \{y^{‘}_1,\dots,y^{‘}_4\} \), состоящей из проекций на регрессионную прямую. Для расчетов вместо дисперсий будем использовать (как и в дисперсионном анализе) суммы квадратов, не деля их на \( 4-1)\). Результат не изменится, поскольку качество предсказания будет измеряться отношением: \( R^2=S_{model}/S_{total} \), где \( S_{total} \) — сумма квадратов для выборки [4] \( \{y_1, \dots, y_4\} \), а \( S_{model} \) — сумма квадратов для выборки \( \{y^{‘}_1, \dots, y^{‘}_4\} \). Роль остатков в \( R^2 \) более понятна, если учесть, что \( S_{model}=S_{total}-S_{error} \) , где \( S_{error} \) — сумма квадратов остатков. Тогда \( R^2=1-S_{error}/S_{total} \).
\( R^2 \)— доля дисперсии выборки, приходящаяся на предсказанные регрессионным уравнением значения y, называется коэффициентом детерминации. Говоря «предсказывается с точностью 60%», мы имели в виду \( R^2 = 0.6 \).
Для простой линейной регрессии \( R^2 \) можно вычислить также, возведя в квадрат коэффициент корреляции: \( R^2=r^2_{xy} \). Доказательство этого факта мы здесь приводить не будем. Для множественной регрессии, о которой речь пойдет дальше, напротив, первичным оказывается \( R^2 \), а множественная корреляция определяется через него.
9.1.5. Стандартизованный регрессионный коэффициент. Значимость
Если в задаче простой линейной регрессии стандартизовать зависимую и независимую переменные, т.е. преобразовать переменные так, чтобы их дисперсии стали равными единице, то регрессионный коэффициент a совпадет с коэффициентом корреляции, а свободный член будет равен нулю, что видно непосредственно из вышеприведенных формул. Статистическая оценка значимости не меняется при допустимом преобразовании шкал, описывающих переменные, поэтому мы будем вести речь о значимости для стандартизованных переменных, поскольку это наиболее удобно.
Во-первых, заметим, что оценка \( R^2 \) не меняется при стандартизации, как и при любом другом линейном преобразовании переменных, поскольку на одинаковые константы умножаются все суммы квадратов \( S_{total} \), \( S_{model} \) и \( S_{error} \). Для оценки значимости аналогично тому, как это делали в дисперсионном анализе, составляется F-отношение:
\[ F=\frac{S_{model}/df_{model}}{S_{error}/df_{error}} \]
Чем больше это отношение, тем больше у нас оснований склониться к тому, что наша модель надежна, и тем уже доверительный интервал вокруг полученного углового коэффициента [5]. Для числителя число степеней свободы равно единице, а для знаменателя n — 2, где n объем выборки (подробнее о степенях свободы в следующем параграфе). Далее — знакомая уже процедура: по полученному значению F находится вес верхнего хвоста соответствующего распределения Фишера, который отсекается данным значением.
Разумеется, значимость регрессионного коэффициента в простой линейной регрессии совпадет со значимостью коэффициента корреляции.
9.1.6. Корреляция, регрессия и причинность
Корреляция и регрессия — инструменты исследования связи, или согласованности двух переменных. Их возможности ограниченны. Сами по себе они никогда не смогут ничего сказать о направлении связи между переменными. Влияет ли уровень оптимизма на продолжительность жизни или, напротив, прогноз состояния организма, каким-то образом воспринимаемый его владельцем, влияет на уровень оптимизма — вопрос, на который нельзя ответить исходя только из корреляционных и регрессионных коэффициентов. Если ответ и возможен, то только с опорой на тонкие аспекты экспериментального дизайна.
>> следующий параграф>>
[1] Здесь также можно различать двухсторонние и односторонние гипотезы, как в случае Т-критерия (см. подпараграф 7.1.5).
[2] Для коэффициента корреляции так же, как и для других статистик, возможен расчет доверительных интервалов, показывающих, какие возможные значения истинной корреляции согласуются с выборочным. Смысл доверительного интервала тот же, что и в разобранных выше случаях, но техника расчета сложнее, поэтому мы не будем ее здесь давать.
[3] В подпараграфе 9.3.1 практикума мы разберем эти операции на конкретном примере. Мы рекомендуем читателю сначала выполнить практическое задание, а затем вернуться к данному пункту.
[4] В главе 7 \( S_{total} \) обозначала у нас сумму квадратов, включая сумму константы, здесь же \( S_{total} \) ее не включает. Это не наш недосмотр, так обозначаются суммы в соответствующих таблицах SPSS, на которые мы здесь ориентируемся. Чтобы уменьшить риск путаницы, мы в первом случае используем заглавную букву ’T’.
[5] Не будем забывать, что наши данные содержат вклад случайных обстоятельств, поэтому при повторении исследования мы можем получить иные коэффициенты.