5.2.1. Среднее выборочное как случайная величина
Напомним, что для случайной величины, заданной таблицей[1]
| X | a1 | a2 | … | an |
| p1 | p2 | … | pn |
математическое ожидание и дисперсия задаются формулами:
\[ M_X=a_1p_1+a_2p_2+\dots+a_np_n \]
\[ D_X=(a_1-M_X)^2p_1+(a_2-M_X)^2p_2+\dots+(a_n-M_X)^2p_n \]
.
Напомним также формулы выборочного среднего и выборочной дисперсии:
\[ \overline{x}=\frac{1}{n}(x_1+x_2+\dots+x_n) \]
\[ S^2_x=\frac{1}{n-1}((x_1-\overline{x})^2+(x_2-\overline{x})^2+\dots+(x_n-\overline{x})^2) \]
В предыдущем параграфе мы говорили, что стандартная ошибка среднего для X, которой измеряется точность оценок, есть стандартное отклонение s, деленное на \( \sqrt{n} \).
Теперь мы разъясним смысл сказанного.
Когда мы планируем оценить средний рост томичей по выборке объема 100, мы заранее заготавливаем форму обработки выборки, которую еще предстоит получить. Можно сказать, что мы предполагаем совершить испытание случайной величины
\[ \overline{X}=\frac{X_1+X_2+\dots+X_{100}}{100} \]
которая представляет собой среднее арифметическое 100 экземпляров случайной величины X: «рост случайного взрослого мужчины-жителя Томска» (обратите внимание, что формула составлена из заглавных букв, которыми мы обозначаем случайные величины). По теореме о сложении дисперсий для суммы независимых случайных величин (см. подпараграф 3.2.5 и приложение 2), дисперсия числителя в правой части в 100 раз больше дисперсии X. Легко также увидеть непосредственно из вида формулы математического ожидания и дисперсии случайной величины, что для любой случайной величины Y/n (в том числе и для стократной суммы одинаковых случайных величин, которая помещена в числителе последней формулы)
\[ M_{Y/n}=\frac{1}{n}M_Y \]
и
\[ D_{Y/n}=\frac{1}{n^2}D_Y \]
Первая формула достаточно очевидна. Используя ее, выводим вторую:
\[ D_{Y/n}=\frac{1}{n-1}[(a_1/n-M_{Y/n})^2p_1+(a_2/n-M_{Y/n})^2p_2+\dots+(a_n/n-M_{Y/n})^2p_n)]= \]
\[ =\frac{1}{n-1}[(\frac{1}{n}(a_1-M_Y))^2p_1+(\frac{1}{n}(a_2-M_Y))^2p_2+\dots+(\frac{1}{n}(a_n-M_Y))^2p_n)]= \]
\[ =\frac{1}{n^2}\frac{1}{n-1}[(a_1-M_Y)^2p_1+(a_2-M_Y)^2p_2+\dots+(a_n-M_Y)^2p_n)]=\frac{1}{n^2}D_Y \]
В таком случае \( M_{\overline{X}}=M_X \) и \( D_{\overline{X}}=\frac{1}{n}D_X \), а следовательно, среднеквадратическое отклонение делится на корень из n: \( \sigma_{\overline{X}}=\sigma_X/\sqrt{n} \) т.е. среднеквадратическое отклонение среднего по n испытаниям случайной величины в \( \sqrt{n} \) раз меньше, чем среднеквадратическое отклонение данной случайной величины. Мы можем сказать теперь, что стандартная ошибка среднего оценивает среднеквадратическое отклонение случайной величины \( \overline{X} \).
Поскольку для любого нормального распределения с математическим ожиданием M и среднеквадратическим отклонением α вероятность попадания в интервал \( (M-\alpha;M+\alpha) \) постоянна (как и вероятности попадания в интервалы с радиусом, равным любому другому фиксированному кратному среднеквадратического отклонения), то среднее арифметическое при увеличении выборки стягивается сужающейся рамкой \( (M-\sigma/\sqrt{x};M+\sigma/\sqrt{x}) \) к реальному математическому ожиданию M.
5.2.2. Доверительный интервал для среднего и значимость. Точные формулы
Пусть для некоторой выборки объема n мы получили \( \overline{x}=a \) и стандартное отклонение, равное s. Чтобы вычислить радиус доверительного интервала, надо сначала найти соответствующий квантиль распределения Стьюдента с \( n-1 \) степенями свободы \( t^{n-1}_\alpha \) (\( \alpha=1-0.95 \) для 95%-го интервала, аналогично для интервалов других «номиналов»). Затем квантиль надо умножить на стандартную ошибку.
Итак, доверительный интервал уровня \( 1-\alpha \) для среднего по выборке объема n это интервал \( (\overline{x}-R_\alpha; \overline{x}+R_\alpha) \), где
\[ R_\alpha=t^{n-1}_\alpha\cdot se=t^{n-1}_\alpha\cdot \frac{s_x}{\sqrt{n}}=t^{n-1}_\alpha\cdot \frac{\sqrt{\frac{1}{n-1}\sum{(x_i-\overline{x})^2}}}{\sqrt{n}} \]
Для оценки значимости гипотезы «истинное среднее равно a» необходимо рассчитать t-статистику по формуле
\[ t=\frac{\overline{x}-a}{se}=\frac{\overline{x}-a}{\sqrt{\frac{1}{n-1}\sum{(x_i-\overline{x})^2}}{}}\sqrt{n} \]
и оценить вес отсекаемого полученным результатом хвоста распределения Стьюдента с n−1 степенями свободы (и затем его удвоить, чтобы получить двухстороннюю значимость)[2].
Упражнение 5.2.2(1). Убедиться, что если \( \overline{x}-a=R_\alpha \), то значимость соответствующей гипотезы «истинное среднее равно a» равна в точности α.
5.2.3. Доверительный интервал для среднего. Точный смысл
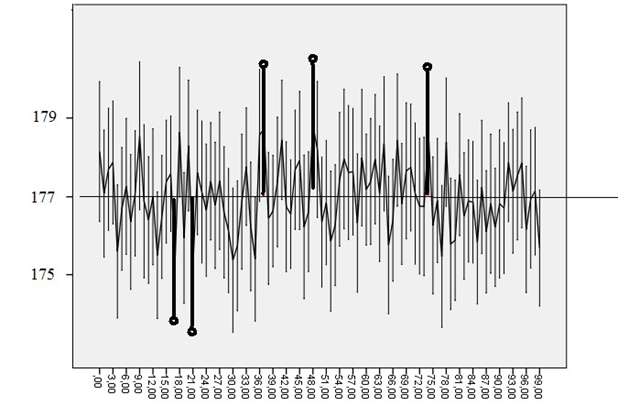
Возьмем выборку объема 121 испытаний нормально распределенной случайной величины с математическим ожиданием 177 и среднеквадратическим отклонением 11. 5-процентный квантиль распределения Стьюдента для 120 степеней свободы равен 1.98 (почти не отличаясь от квантиля нормального распределения, как мы говорили). Стандартная ошибка для получаемых случайных выборок будет колебаться около \( 11/\sqrt{121} \), т.е. вокруг единицы. Таким образом, радиус доверительного интервала будет колебаться около 1.98. На рис. 5.2.3(1). показаны результаты 100 испытаний такой процедуры: порождалась выборка объема 121, оценивалось стандартное отклонение, вычислялся доверительный интервал и он изображался вертикальным отрезком. Жирными линиями выделены те экземпляры доверительных интервалов, которые не накрыли математическое ожидание 177.
Рис. 5.2.3(1). Результат моделирования последовательного порождения выборок объема 121 испытаний нормальной случайной величины с математическим ожиданием 177 и среднеквадратическим отклонением 11. Построено 100 доверительных интервалов. Жирной линией выделены те, которые не накрывают математическое ожидание 177
В литературе встречаются следующие интерпретации доверительного интервала (не все они правильные):
- 95%-й доверительный интервал для среднего с вероятностью 0.95 накрывает истинное математическое ожидание.
- Истинное математическое ожидание с вероятностью 0.95 содержится в доверительном интервале.
- 95% средних значений новых выборок попадут в полученный нами интервал.
Истинность первого утверждения мы можем проиллюстрировать нашим примером на рис. 5.2.3(1). Действительно, если математическое ожидание нам известно, то 95%-й доверительный интервал будет накрывать его в среднем в 95% случаев.
Вторая формулировка тем не менее не истинна: если мы получили какой-то доверительный интервал, то ничего о вероятности попадания истинного математического ожидания в этот интервал мы сказать не можем. Прежде всего, потому что истинное математическое ожидание не является случайной величиной [3]. Далее, если вы знаете истинное математическое ожидание роста случайно выбранного жителя Томска, а я оцениваю его по выборке, то вы всегда знаете, получил ли я «счастливый» или «несчастливый» интервал, а я не могу этого знать. В «несчастливом» случае на мое заявление «истинное математическое ожидание с вероятностью 0.95 содержится в (полученном мной) доверительном интервале» вы со стопроцентной уверенностью скажете, что оно там не содержится и никогда не будет содержаться.
Третья формулировка ложна в силу тех же обстоятельств. «Несчастливый» интервал накрывает меньше даже той половины оси, в которой он разместился. Вероятность попадания среднего в другую половину оси равна 0.5. Несчастливый интервал не обещает даже 50-процентной вероятности попадания в него будущих средних выборочных.
Итак, верно лишь первое утверждение — в том смысле, который прояснен на рис. 5.2.3(1): известное кому-то (в худшем случае, одному богу) математическое ожидание накрывается доверительным интервалом с соответствующей вероятностью.
Следующая формулировка еще точнее: если мы собираемся оценить истинное среднее по выборке, то вероятность того, что 95%-й доверительный интервал, который мы по выборке построим, накроет истинное среднее, равна 0.95. Здесь важно, что вероятность вообще касается только тех событий, которые еще не произошли.
>> следующий параграф>>
[1] В таблице мы обозначили возможные значения случайной величины буквами a, чтобы отличать их от результатов испытаний этой случайной величины (выборочных значений), по-прежнему обозначаемых буквами x.
[2] Если в последней формуле заменить строчные буквы x заглавными, то полученная формула задаст случайную величину, подобно тому, как в предыдущем параграфе рассматривалась как случайная величина. Напомним: при большом объеме выборки эта случайная величина имеет стандартное нормальное распределение. Если выборка невелика, то распределение «расплывается» (как изображено на рис. 5.1.3(2)) и квантили надо определять по соответствующим распределениям Стьюдента.
[3] Только в искусственных ситуациях можно сделать истинное математическое ожидание случайной величиной, но это потребует задать его априорное распределение.