Рассмотрим пример использования двухфакторного дисперсионного анализа в психологическом исследовании.
Пример 8.3(1). В файле TeacherExp.sav (версия для SPSS, версия для Jamovi) содержатся данные, моделирующие результаты исследования, описанного в подпараграфе 8.1.3.
В файле данных первый столбец (ТeacherExp) содержит информацию об опыте преподавателя, второй (StudMotivation) — о мотивации студента и, наконец, третий — балл, характеризующий уровень знаний после прослушивания курса.
Теперь мы опишем, как проводится двухфакторный дисперсионный анализ в SPSS.
Для вызова этой процедуры следует выбрать пункты меню Анализ — Общая линейная модель — ОЛМ-одномерная (Analyze — General Linear Model — Univariate). В появившемся диалоговом окне в поле Зависимая переменная (Dependent Variable) внесем нашу зависимую переменную (Results), а в поле Фиксированные факторы (Fixed Factor(s)) два фактора: ТeacherExp и StudMotivation[1].
Чтобы построить графики, выбираем Графики (Plots), затем в поле Горизонтальная ось (Horizontal Axis) вносим переменную ТeacherExp. После этого нажимаем кнопку Добавить (Add). Этими действиями задается график вклада фактора опыта преподавателя. Для отображения вклада второго фактора в поле Горизонтальная ось (Horizontal Axis) вносим переменную StudMotivation, после чего нажимаем кнопку Добавить (Add). И наконец, для построения графика, отображающего взаимодействие факторов, в поле Горизонтальная ось (Horizontal Axis) вносим переменную StudMotivation, а в поле Отдельные линии (Separate Lines) — переменную ТeacherExp, после чего нажимаем кнопку Добавить (Add). Для завершения процедуры задания графиков нажмем кнопку Продолжить (Continue).
Заметим, что график взаимодействия факторов можно задать с переменной ТeacherExp в поле Отдельные линии (Separate Lines), а переменную StudMotivation поместить в поле Горизонтальная ось (Horizontal Axis). Вся нужная информация содержится в обоих графиках, но иногда они не одинаково наглядно ее представляют. Можно посоветовать рисовать сначала оба графика, а затем выбрать более наглядный для представления результатов.
Если теперь нажать OK и запустить расчет, мы получим следующие таблицы и графики.
Первая таблица «Межгрупповые факторы» содержит информацию о количестве факторов, их уровнях и количестве испытуемых на каждом из уровней фактора. Она не нуждается в пояснениях.
Вторая таблица (8.3(2)) содержит информацию о суммах квадратов и значимостях.
Таблица 8.3(2). Результат двухфакторного дисперсионного анализа в SPSS
| Оценка эффектов межгрупповых факторов | |||||
| Зависимая переменная: Уровень знаний по предмету | |||||
| Иcточник | Сумма квадратов типа III | ст. св. | Средний квадрат | F | Знч. |
| Скорректированная модель | 648.000a | 8 | 81.000 | 40.500 | 0.000 |
| Свободный член | 2187.000 | 1 | 2187.000 | 1093.500 | 0.000 |
| TeacherExp | 162.000 | 2 | 81.000 | 40.500 | 0.000 |
| StudMotivation | 450.000 | 2 | 225.000 | 112.500 | 0.000 |
| TeacherExp * StudMotivation | 36.000 | 4 | 9.000 | 4.500 | 0.011 |
| Ошибка | 36.000 | 18 | 2.000 | ||
| Всего | 2871.000 | 27 | |||
| Скорректированный итог | 684.000 | 26 | |||
| a. R квадрат = 0.947 (Скорректированный R квадрат = 0.924) | |||||
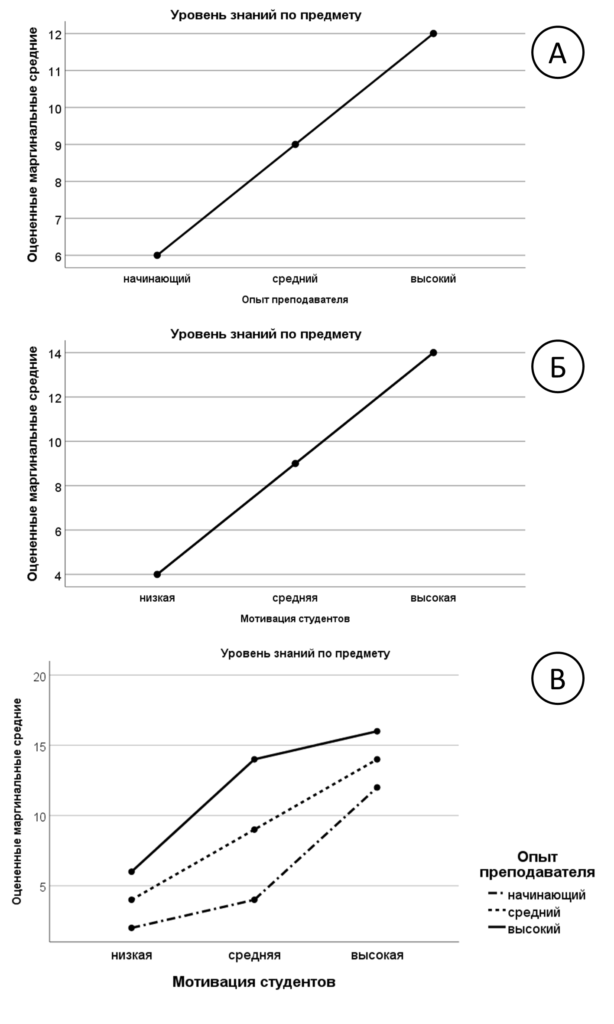
Рис. 8.3(3). Графики среднего для влияния факторов по отдельности (А, Б) и их взаимодействия (В).
Первая строка таблицы — «Скорректированный итог» оценивает общее влияние совокупности всех включенных в анализ факторов (в нашем случае — опыт преподавателя, мотивация студентов и их взаимодействие). Вторая строка «Свободный член» относится к оценке отличия от нуля общего среднего по всей выборке и носит скорее технический характер, содержательно эти данные интерпретируются довольно редко. Нас интересуют, прежде всего, три строка с описанием влияния двух факторов и их взаимодействия. Строка в таблице, описывающая значимость по переменной TeacherExp, соотносится с первым графиком аналогично однофакторному дисперсионному анализу. Надо только иметь в виду, что каждая точка графика отображает усредненные по всем значениям второго фактора StudMotivation, результаты в данной точке. Следующая строка относится ко второму графику, а третья строка, подписанная TeacherExp*StudMotivation относится к третьему графику. Интерпретацию этого графика мы давали в подпараграфе 8.1.3.
Можно добавить к выводу апостериорные сравнения (по каждому фактору в отдельности) аналогично однофакторному анализу, а с помощью дополнительного окна, вызываемого кнопкой Параметры (Options) можно задать расчеты различных показателей зависимой переменной на разных уровнях факторов. Чтобы задать расчет средних значений по всем параметрам на всех уровнях обоих факторов, надо отметить пункт Описательная статистика (Descriptive Statistics) . Выводимая в результате таблица средних проста и не нуждается в пояснениях.
Теперь мы опишем, как проводится двухфакторный дисперсионный анализ в Jamovi.
Для вызова этой процедуры следует выбрать пункты меню ANOVA — ANOVA. В появившемся диалоговом окне в поле Dependent Variable внесем нашу зависимую переменную (Results), а в поле Fixed Factors два фактора: ТeacherExp и StudMotivation[1]. Также сразу для оценки не только уровня значимости F-отношения, но и силы эффекта следует отметить один из типов оценки силы эффекта. В Jamovi реализовано три коэффициента — эта-квадрат\( \eta^2 \), частная эта-квадрат \( \eta^2_p \) и омега \( \omega \). Для многофактороного дисперсионного анализа наиболее распространенным вариантом является \( \eta^2_p \), позволяющий оценить влияние отдельного фактора (то есть долю объясняемой им дисперсии), остающейся после исключения влияния других факторов (дисперсии, объясненной другими факторами). Также при желании, для оценки общего влияния факторов и их взаимодействия можно отметить пункт Overall model test.
После заполнения этих полей программа рассчитает основную базовую таблицу дисперсионного анализа, она представлена ниже.
Таблица 8.3(1)j. Результат двухфакторного дисперсионного анализа в Jamovi.
| ANOVA — Results | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sum of Squares | df | Mean Square | F | p | η²p | ||||||||
| Overall model | 648.0000 | 8 | 81.0000 | 40.5000 | < .001 | ||||||||
| TeacherExp | 162.0000 | 2 | 81.0000 | 40.5000 | < .001 | 0.8182 | |||||||
| StudMotivation | 450.0000 | 2 | 225.0000 | 112.5000 | < .001 | 0.9259 | |||||||
| TeacherExp ✻ StudMotivation | 36.0000 | 4 | 9.0000 | 4.5000 | 0.011 | 0.5000 | |||||||
| Residuals | 36.0000 | 18 | 2.0000 | ||||||||||
Таблица содержит следующие столбцы: Оцениваемый компонент модели, соответствующие им суммы квадратов (Sum of Squares), степени свободы (df), средние квадраты (Mean Square), F-отношение(F), уровень значимости(p) и силу эффекта частного эта-квадрат (η²p).
Первая строка таблицы — «Overall model» оценивает общее влияние совокупности всех включенных в анализ факторов (в нашем случае — опыт преподавателя, мотивация студентов и их взаимодействие). Следующие три строки, которые позволяют оценить влияния двух факторов и их взаимодействия. Строка в таблице, описывающая значимость по переменной TeacherExp относится к влиянию фактора опыта преподавателя — и этот эффект оказывается значимым и сильным, отчёт об этом результате может выглядеть так: \( F(2, 18) = 40.500, p < 0.001,\eta^2_p=0.818 \)). В следующих двух строках находятся оценки влияния второго фактора и взаимодействия.
Следует заметить, что само по себе F-отношение ничего не сообщает о характере влияния фактора, то есть, эта таблица говорит о том, что и оба фактора, и их взаимодействие влияет на зависимую переменную, но ничего не сообщает о том, каково направление этого влияния. Для оценки этого нужно проанализировать соотношение средних значений в группах испытуемых.
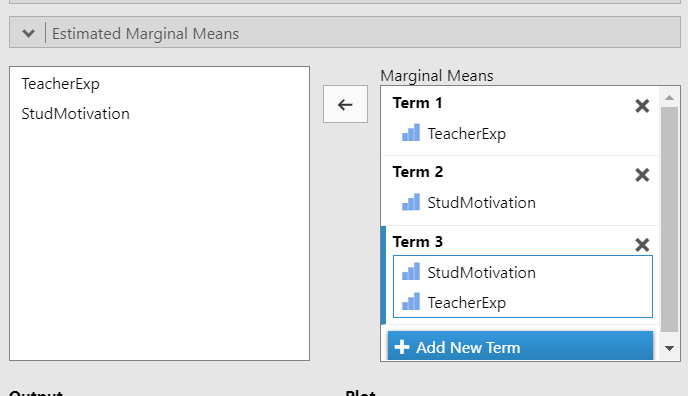
Для этого в Jamovi можно зайти в раздел Estimated Marginal Means. Там, во-первых, можно вывести графики средних с ошибками средних. Так как у нас в примере оценивается три эффекта, можно нарисовать три графика: результаты, усредненные только по группам с преподавателями с разным опытом, затем только по группам с разной мотиваций, и, наконец, для их взаимодействия. Для этого нужно задать первый график, перенеся переменную ТeacherExp в поле Marginal Means, раздел Term 1. Затем, для добавления графика средних в группах по мотивации надо добавить его, нажав кнопку + Add New Term и перенести в появившееся поле второй фактор StudMotivation. Наконец, можно добавить и третий график, включающий в себя оба фактора. Заполненное окно приведено на рис. 8.3.(2)j
Рис. 8.3(2)j. Заполненное окно для отображения графиков средних.
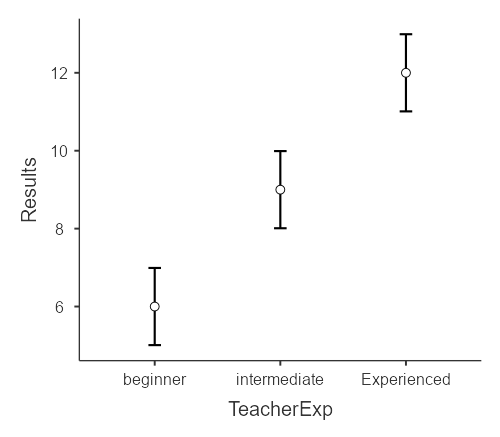
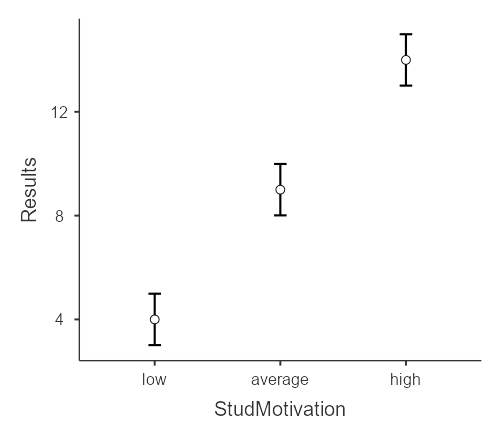
В результаты программа выведет три графика, позволяющих описать, что происходит с зависимой переменной в зависимости от уровней факторов.
Рис. 8.3(3)j. Графики среднего для влияния факторов по отдельности (А, Б) и их взаимодействия (В) в Jamovi.
Опишем, как проводится двухфакторный дисперсионный анализ в R.
Расчёт дисперсионного анализа с двумя и более факторами в R можно провести с помощью уже известной из предыдущей главы функции aov. При наличии нескольких факторов они записываются в формулу анализа через знак * (если в модель включается возможность взаимодействия) или знак + (если оценка взаимодействия влияния факторов не подразумевается и не закладывается в модель). Соответственно, в рассматриваемом примере формула для дисперсионного анализа, включающего оценку влияния факторов «опыт преподавателя (переменная ТeacherExp) и мотивации студентов (переменная StudMotivation) на успеваемость (переменная Result) будет выглядеть так: Results ~ TeacherExp * StudMotivation. Если данные загрузить в таблицу data_teachExp, то провести дисперсионный анализ и получить базовый результат можно используя следующий набор команд:
library(foreign)
data_teachExp <- read.spss("TeacherExp.sav", to.data.frame = T, reencode = "utf8")
model <- aov(Results ~ TeacherExp * StudMotivation, data = data_teachExp)
summary(model)
Результат будет следующим:
Df Sum Sq Mean Sq F value Pr(>F) TeacherExp 2 162 81 40.5 2.17e-07 *** StudMotivation 2 450 225 112.5 6.71e-11 *** TeacherExp:StudMotivation 4 36 9 4.5 0.0107 * Residuals 18 36 2 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Таблица результатов содержит следующие столбцы: в начале указан оцениваемый компонент модели, затем для каждого из них указаны степени свободы (Df), суммы квадратов (Sum Sq), средние квадраты (Mean Sq), F-отношение (F value) и уровень значимости(Pr(>F)).
Первая строка таблицы относится к оценке влияния фактора TeacherExp, то есть опыта преподавателя — и этот эффект оказывается значимым, отчёт об этом результате может выглядеть так: F(2,18)=40.500, p<0.001). В следующих двух строках находятся оценки влияния второго фактора (мотивации студентов) и взаимодействия этих двух факторов.
Следует заметить, что само по себе F-отношение ничего не сообщает о характере влияния фактора, то есть, эта таблица говорит о том, что и оба фактора, и их взаимодействие заметно влияет на зависимую переменную, но ничего не сообщает о том, каково направление этого влияния. Для оценки этого нужно проанализировать соотношение средних значений в группах испытуемых.
Самый простой вариант получения средних значений зависимой переменной в группах можно получить с помощью функции model.tables, указав в качестве первого аргумента имя рассчитанной выше модели, а второго – тип таблицы ‘means’.
model.tables(model, 'means')
В результате будет получены четыре таблицы – с общим средним, усреднёнными оценками в зависимости от каждого фактора по отдельности и с оценками в зависимости от сочетания факторов:
Tables of means Grand mean 9 TeacherExp TeacherExp начинающий средний высокий 6 9 12 StudMotivation StudMotivation низкая средняя высокая 4 9 14 TeacherExp:StudMotivation StudMotivation TeacherExp низкая средняя высокая начинающий 2 4 12 средний 4 9 14 высокий 6 14 16
Таким образом, можно увидеть, что, например, усредненная успеваемость для низкого, среднего и высокого уровня опыта преподавателя (независимо от мотивации студентов) составляет 6, 9 и 12 баллов. Если учитывать оба фактора, то успеваемость студентов с низкой мотивацией, обучающихся у преподавателя с низким уровнем опыта составляет 2 балла, при обучении у преподавателя со средним уровнем опыта такие студенты получают 4 балла, у преподавателя с большим опытом – 6 баллов и так далее.
Полученные таблицы содержат только средние арифметические, в них нет важной информации о вариативности (дисперсии) данных внутри групп. Эту информацию можно поучить с помощью известной нам функции describeByиз пакетаpsych, использовав формулу Results ~ TeacherExp + StudMotivation, так как в синтаксисе этой функции специально указывать на взаимодействие факторов не требуется. Также для удобства чтения результата его лучше выводит в формате матрицы (аргумент mat=TRUE) и не рассчитывать дополнительные статистики, такие как асимметрия и эксцесс (установив аргумент fast=TRUE):
describeBy(Results ~ TeacherExp + StudMotivation, data = data_teachExp, mat=TRUE, fast=TRUE)
Полученный результат будет следующим:
item group1 group2 vars n mean sd min max range se X11 1 начинающий низкая 1 3 2 1 1 3 2 0.5773503 X12 2 средний низкая 1 3 4 1 3 5 2 0.5773503 X13 3 высокий низкая 1 3 6 2 4 8 4 1.1547005 X14 4 начинающий средняя 1 3 4 1 3 5 2 0.5773503 X15 5 средний средняя 1 3 9 2 7 11 4 1.1547005 X16 6 высокий средняя 1 3 14 1 13 15 2 0.5773503 X17 7 начинающий высокая 1 3 12 2 10 14 4 1.1547005 X18 8 средний высокая 1 3 14 1 13 15 2 0.5773503 X19 9 высокий высокая 1 3 16 1 15 17 2 0.5773503
В этой таблице столбец group1 соответствует группировке по опыту учителя, а group2 – группировке по мотивации студентов. Соответственно, средние (столбец mean) совпадают с таблицей средних при учёте обоих факторов, но также далее приведено стандартное отклонение (столбец sd), и стандартная ошибка среднего (столбец se).
Также бывает удобно и полезно визуализировать описательную статистику. Для этого в R можно использовать довольно много различных функций, мы опишем две. Первая – это известная нам из предыдущих глав функция error.bars.by. Ниже приведены три команды, позволяющих вывести графики средних со столбиками ошибок – 95% доверительным интервалом средних – для оценки влияния факторов по отдельности и их взаимодействия:
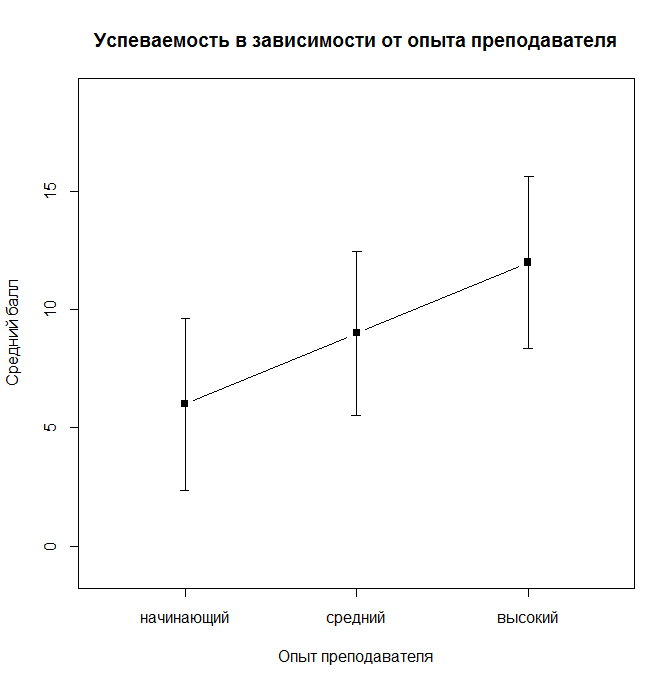
error.bars.by(Results ~ TeacherExp, data = data_teachExp, eyes = F, main = "Успеваемость в зависимости от опыта преподавателя", v.labels = levels(data_teachExp$TeacherExp), xlab="Опыт преподавателя", ylab="Средний балл")
Рис. 8.3(1)j. Средняя успеваемость в зависимости от опыта преподавателя
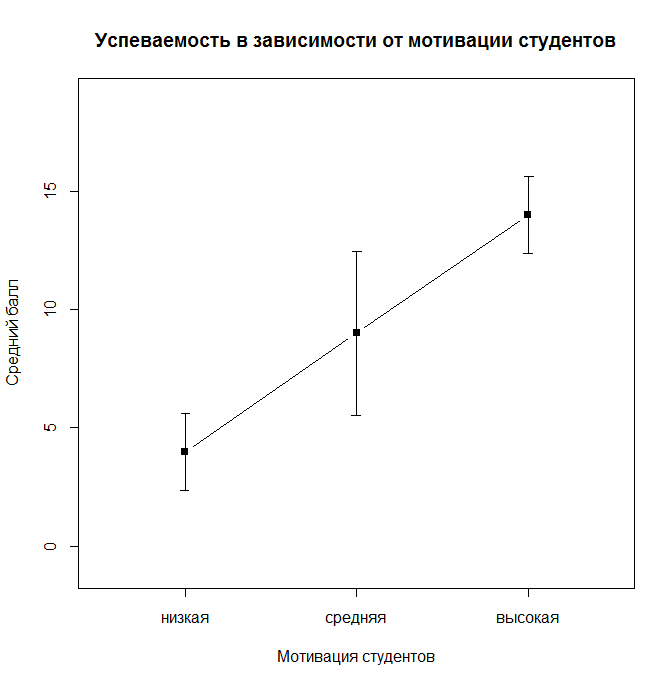
error.bars.by(Results ~ StudMotivation, data = data_teachExp, eyes = F, main = "Успеваемость в зависимости от мотивации студентов", v.labels = levels(data_teachExp$StudMotivation), xlab="Мотивация студентов", ylab="Средний балл")
Рис. 8.3(2)j. Средняя успеваемость в зависимости от мотивации студентов
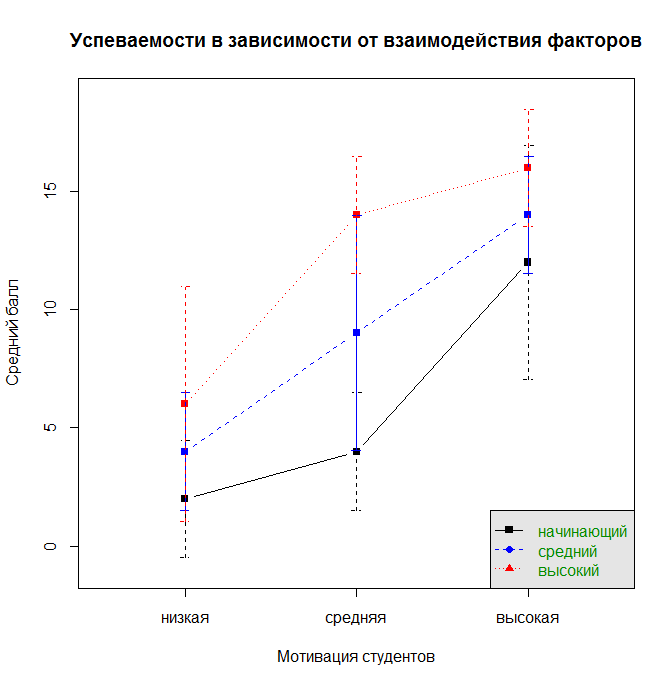
error.bars.by(Results ~ StudMotivation + TeacherExp, data = data_teachExp, eyes = F, main = "Успеваемости в зависимости от взаимодействия факторов", legend = 1, v.labels = levels(data_teachExp$StudMotivation), labels = levels(data_teachExp$TeacherExp), xlab="Мотивация студентов", ylab="Средний балл")
Рис. 8.3(3)j. Средняя успеваемость при совместном учёте опыта преподавателя и мотивации студентов
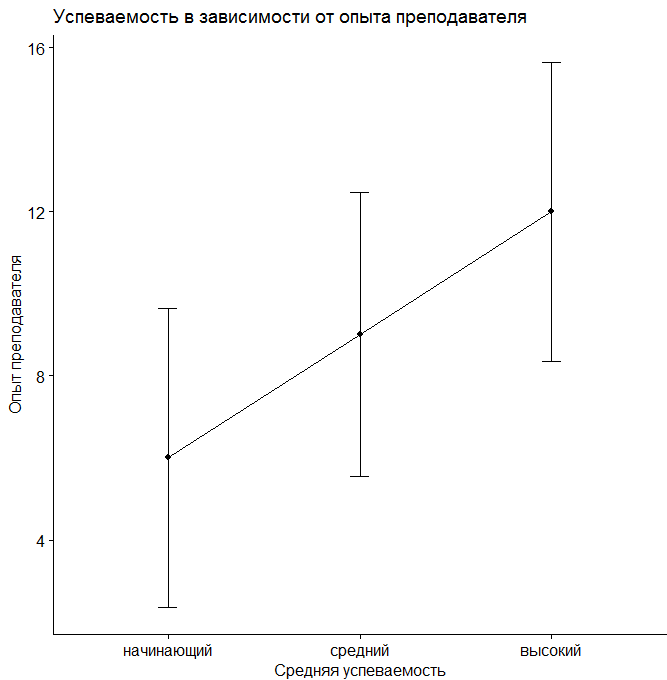
Второй способ построения графиков, который мы кратко опишем – более гибкий, основанный на графической системе ggplot(библиотеки ggplot2). Прямое использование функции ggplotтребует отдельного изучения, в качестве упрощенного варианта мы предлагаем читателю познакомиться с функцией gglineиз пакета ggpubr, предназначенного для подготовки графиков для научных публикаций. В функции ggline надо указать в качестве первого аргумента таблицу данных. Затем аргумент x – название переменной, соответствующей фактору, который будет отображен на оси X, y – название усредняемой (зависимой) переменной. Для отображения 95% доверительного интервала среднего необходимо добавить аргумент add = «mean_ci», затем можно ввести более информативные подписи осей и заглавие (по умолчанию подписи осей – названия переменных, а заголовок отсутствует).
library(ggpubr) ggline(data_teachExp, x = "TeacherExp", y = "Results", add = "mean_ci", xlab="Средняя успеваемость", ylab= "Опыт преподавателя", title = "Успеваемость в зависимости от опыта преподавателя")
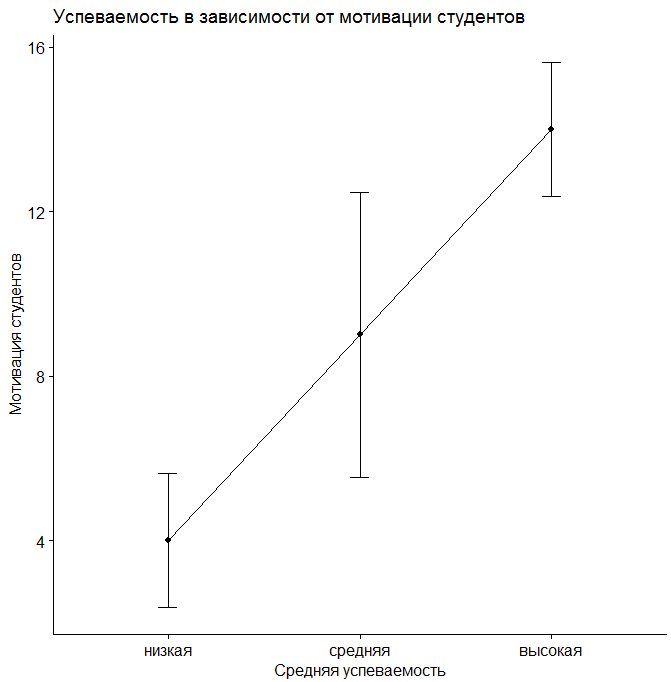
ggline(data_teachExp, x = "StudMotivation", y = "Results", add = "mean_ci", xlab="Средняя успеваемость", ylab= "Мотивация студентов", title = "Успеваемость в зависимости от мотивации студентов")
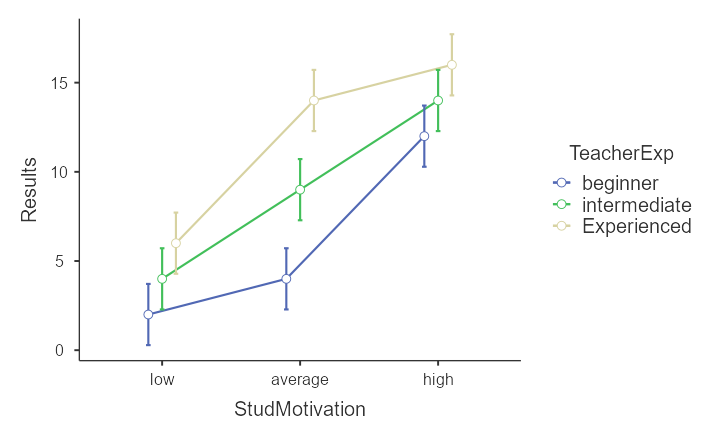
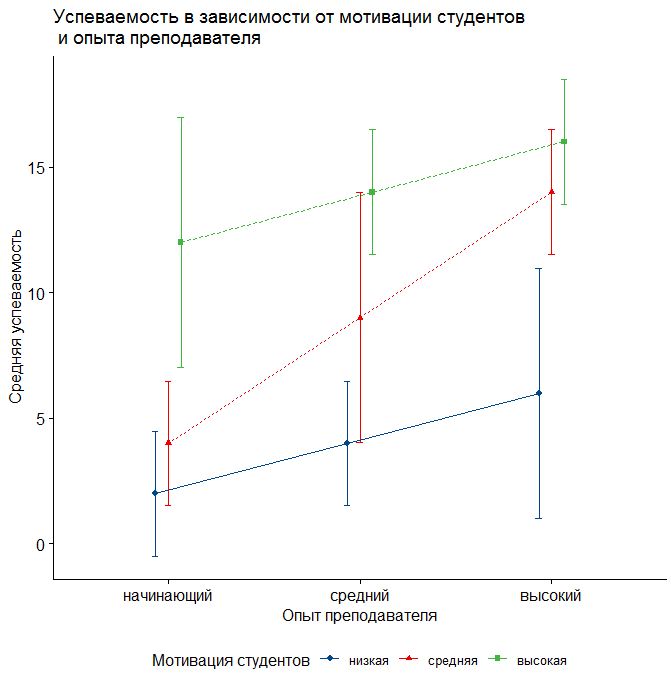
При введении второго фактора, соответствующего отдельным линиям, добавляется аргумент linetype с указанием названия переменной – второго фактора, также можно отобразить средние разными маркерами, указав аналогично аргумент shape, а также отобразить линии разным цветом, использовав аргумент color. Цветовой палитрой можно управлять, напрямую указывая цвета (в виде вектора), либо используя наборы стандартных цветов, в нашем примере мы использовали стандартные цвета для публикации в известном медицинском журнале lancet. Другие варианты палитр (а также множество дополнительных настроек графика) можно найти в документации функции, использовав команду help. Мы добавили ещё аргумент position, присвоив ему функцию position_dodge(0.2), которая «раздвигает» средние по оси X таким образом, чтобы доверительные интервалы не накладывались друг на друга? А также переместили легенду вниз графика. Дополнительно мы изменили заголовок легенды с помощью функцииggpar:
ggline(data_teachExp, x = "TeacherExp", y = "Results", color = "StudMotivation", linetype = "StudMotivation", shape = "StudMotivation", add = "mean_ci", xlab="Опыт преподавателя", ylab= "Средняя успеваемость", title = "Успеваемость в зависимости от мотивации студентов\n и опыта преподавателя", palette = "lancet", position = position_dodge(.2), legend = "bottom") %>% ggpar(legend.title = "Мотивация студентов")
Ещё один вопрос, на котором стоит остановиться в этом примере – это попарные сравнения групп испытуемых. Такое сравнение с поправкой Тьюки можно получить с помощью функции TukeyHSD, указав в качестве аргумента рассчитанную модель. По умолчанию при выполнении этой команды будут выведены попранные сравнения как групп, образованных факторами по отдельности, так и во взаимодействии:
TukeyHSD(model) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = Results ~ TeacherExp * StudMotivation, data = data_teachExp) $TeacherExp diff lwr upr p adj средний-начинающий 3 1.298558 4.701442 7.71e-04 высокий-начинающий 6 4.298558 7.701442 1.00e-07 высокий-средний 3 1.298558 4.701442 7.71e-04 $StudMotivation diff lwr upr p adj средняя-низкая 5 3.298558 6.701442 1.8e-06 высокая-низкая 10 8.298558 11.701442 0.0e+00 высокая-средняя 5 3.298558 6.701442 1.8e-06 $`TeacherExp:StudMotivation` diff lwr upr p adj средний:низкая-начинающий:низкая 2.000000e+00 -2.04591141 6.045911 0.7212884 высокий:низкая-начинающий:низкая 4.000000e+00 -0.04591141 8.045911 0.0540285 начинающий:средняя-начинающий:низкая 2.000000e+00 -2.04591141 6.045911 0.7212884 средний:средняя-начинающий:низкая 7.000000e+00 2.95408859 11.045911 0.0002709 высокий:средняя-начинающий:низкая 1.200000e+01 7.95408859 16.045911 0.0000001 начинающий:высокая-начинающий:низкая 1.000000e+01 5.95408859 14.045911 0.0000023 средний:высокая-начинающий:низкая 1.200000e+01 7.95408859 16.045911 0.0000001 высокий:высокая-начинающий:низкая 1.400000e+01 9.95408859 18.045911 0.0000000 высокий:низкая-средний:низкая 2.000000e+00 -2.04591141 6.045911 0.7212884 начинающий:средняя-средний:низкая -1.332268e-15 -4.04591141 4.045911 1.0000000 средний:средняя-средний:низкая 5.000000e+00 0.95408859 9.045911 0.0093912 высокий:средняя-средний:низкая 1.000000e+01 5.95408859 14.045911 0.0000023 начинающий:высокая-средний:низкая 8.000000e+00 3.95408859 12.045911 0.0000506 средний:высокая-средний:низкая 1.000000e+01 5.95408859 14.045911 0.0000023 высокий:высокая-средний:низкая 1.200000e+01 7.95408859 16.045911 0.0000001 начинающий:средняя-высокий:низкая -2.000000e+00 -6.04591141 2.045911 0.7212884 средний:средняя-высокий:низкая 3.000000e+00 -1.04591141 7.045911 0.2528714 высокий:средняя-высокий:низкая 8.000000e+00 3.95408859 12.045911 0.0000506 начинающий:высокая-высокий:низкая 6.000000e+00 1.95408859 10.045911 0.0015645 средний:высокая-высокий:низкая 8.000000e+00 3.95408859 12.045911 0.0000506 высокий:высокая-высокий:низкая 1.000000e+01 5.95408859 14.045911 0.0000023 средний:средняя-начинающий:средняя 5.000000e+00 0.95408859 9.045911 0.0093912 высокий:средняя-начинающий:средняя 1.000000e+01 5.95408859 14.045911 0.0000023 начинающий:высокая-начинающий:средняя 8.000000e+00 3.95408859 12.045911 0.0000506 средний:высокая-начинающий:средняя 1.000000e+01 5.95408859 14.045911 0.0000023 высокий:высокая-начинающий:средняя 1.200000e+01 7.95408859 16.045911 0.0000001 высокий:средняя-средний:средняя 5.000000e+00 0.95408859 9.045911 0.0093912 начинающий:высокая-средний:средняя 3.000000e+00 -1.04591141 7.045911 0.2528714 средний:высокая-средний:средняя 5.000000e+00 0.95408859 9.045911 0.0093912 высокий:высокая-средний:средняя 7.000000e+00 2.95408859 11.045911 0.0002709 начинающий:высокая-высокий:средняя -2.000000e+00 -6.04591141 2.045911 0.7212884 средний:высокая-высокий:средняя 0.000000e+00 -4.04591141 4.045911 1.0000000 высокий:высокая-высокий:средняя 2.000000e+00 -2.04591141 6.045911 0.7212884 средний:высокая-начинающий:высокая 2.000000e+00 -2.04591141 6.045911 0.7212884 высокий:высокая-начинающий:высокая 4.000000e+00 -0.04591141 8.045911 0.0540285 высокий:высокая-средний:высокая 2.000000e+00 -2.04591141 6.045911 0.7212884
Первый блок результатов ($TeacherExp) содержит сравнение средних групп, выделенных только по опыту учителя, второй ($StudMotivation) – сравнение трех групп студентов, а последняя – все возможные сравнения групп, выделенных при учёте обоих факторов.
Упражнение 8.3(3)j. Найдите две наиболее слабо различающиеся и две максимально различающиеся группы.
Ответ. Минимальное различие средних получено между группой обучающейся у начинающего преподавателя и средней мотивацией и обучающейся у преподавателя со средним опытом и низкой мотивацией (строка начинающий:средняя-средний:низкая, p=1.000). Максимальное отличие получено между группой, обучающихся у начинающего преподавателя с низкой мотивацией и группой, обучающейся у опытного преподавателя с высокой мотивацией (строка высокий:высокая-начинающий:низкая, p < 0.000001).
Пример 8.3(4). В файле Dominance.sav (версия для SPSS, версия для Jamovi) представлены данные, моделирующие результаты, описанные в подпараграфе 8.1.4.
Упражнение 8.3(5). Проведите двухфакторный дисперсионный анализ. Нарисуйте графики. Найдите способ повторить график, изображенный на рис. 8.1.4(1). Найдите соответствующую каждому графику значимость результата.
Пример 8.3(6). В файле YerksDodson.sav (версия для SPSS, версия для Jamovi) приведены модельные данные для эксперимента, описанного в подпараграфе 8.1.5.
Упражнение 8.3(7). Проведите двухфакторный дисперсионный анализ и сопоставьте график рисунка 8.1.5(1) и полученный с помощью используемого статистического пакета. Объясните различия.
>> следующий параграф>>
[1] В поле «Фиксированные факторы» технически можно внести и большее количество переменных, однако на практике в дисперсионный анализ редко включается больше трех факторов. Действительно, уже в случае трех независимых переменных придется рассмотреть семь возможных влияний (каждой переменной в отдельности, попарных взаимодействий и взаимодействия всех факторов). В случае же четырех факторов результаты статистической обработки становится крайне сложно интерпретировать. В рамках нашего учебника мы будем рассматривать примеры только с двумя независимыми переменными, однако при увеличении их числа результаты интерпретируются аналогично.