2.1.1. Что такое «случайность»? Что в психологии может считаться случайным?
Мы легко пользуемся словом «случайность» в обыденной речи. Случайным обычно называется результат влияния неконтролируемых побочных обстоятельств на какой-то интересующий нас процесс.
Иногда случайность специально культивируется. В азартных играх это — перемешивание карт, встряхивание костей в стаканчике и т.п. Бросание жребия — еще один пример организации случайного результата. В таких случаях оказывается, что в массовых процессах, связанных с организованной случайностью, выявляются некоторые закономерные тенденции, которые в принципе можно учитывать при планировании деятельности. Например, используя случайность, можно с достаточной надежностью делать выводы о результатах выборов, опрашивая не всех проголосовавших, а только некоторую часть из них, что и делают социологические службы, чтобы оценить результаты до официального их объявления. Оценки такого рода опираются на относительно узкое понятие случайности, связанное с повторениями одинаково организованных процедур, приводящих к результатам из определенной совокупности возможностей. Именно такое использование случайности в психологических исследованиях мы и будем рассматривать в нашей книге.
Если исследователь хочет узнать, как влияют на время реакции человека различные экспериментальные условия, он берет в качестве испытуемых не всех живущих на Земле людей, а группу «случайных» представителей человеческого рода. Как можно реализовать такой случайный выбор? Можно, например, сделать огромный барабан (похожий на тот, который используется в телеигре «Поле чудес», только несравненно больший по размерам), по краю которого выписать фамилии всех жителей Земли. Раскрутив его достаточно сильно, будем ждать, на кого укажет стрелка. Если список граждан хранится в какой-нибудь компьютерной базе данных, то случайный выбор еще проще организовать, используя специальные компьютерные средства. Однако физическая реализуемость — не главное для нас. Нам важно сейчас представить себе идеальную равновозможность появления имени каждого гражданина по нашему запросу и извлечь статистические следствия из этого представления.
На самом деле исследователю приходится довольствоваться совсем не безупречными процедурами случайного выбора. Например, он может повесить объявление в коридоре университета и привлечь студентов-добровольцев. Если по времени реакции студенты еще могут считаться случайными представителями человечества в данных условиях, то по уровню интеллекта они, разумеется, таковыми считаться уже не могут, так как прошли солидные образовательные процедуры и отбор. Мы не будем в нашем учебнике специально обсуждать эти вопросы, но при проведении исследований и обследований законность и обоснованность выбора испытуемых надо иметь в виду.
Если нам удается приемлемым образом решить вопрос выбора для исследования в удовлетворительном смысле случайных людей, то возникает второй вопрос: какие выводы о психологии человека мы можем тогда делать из наших экспериментальных результатов? Чтобы узнать ответ на этот вопрос, надо изучить статистику.
2.1.2. Генеральная совокупность и распределение
Начнем с уточнений и идеализаций. Пусть у нас есть множество людей, некоторая характеристика которых нас интересует. Например, мы исследуем тревожность россиян, используя определенную тестовую методику.
Определение 2.1.2(1). Будем называть генеральной совокупностью множество значений определенной характеристики, принадлежащей представителям некоторой совокупности индивидов [1].
Если нас интересует тревожность россиян, то генеральной совокупностью будут все граждане России, точнее, их тревожность.
Определение 2.1.2(2). Выборкой будем называть некоторую, обычно относительно небольшую и обозримую часть этого множества.
Определение 2.1.2(3) Будем называть выборку случайной, если члены выборки представляют собой случайно отобранных представителей интересующей нас генеральной совокупности.
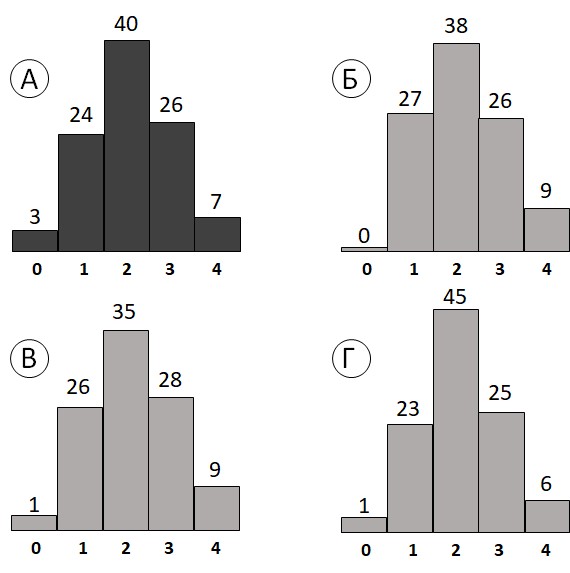
Если бы каким-то образом нам стали известны результаты тестирования каждого представителя генеральной совокупности, каждого нашего согражданина, то с такой информацией нам было бы очень трудно работать — она необозрима. Можно было бы попросить того, от кого мы ее получили, дать более компактное ее представление. Например, если результаты тестирования нашей методикой измерения тревожности могут изменяться от 0 (не тревожный) до 4 (очень тревожный), то одним из таких компактных представлений будет таблица частот, где для каждой из возможных оценок рассчитан процент людей, которые эту оценку получили. Возможный результат представлен в таблице 2.1.2(4).
Таблица 2.1.2(4). Возможный результат тестирования
| Распределение результатов тестирования | |||||
| Результаты тестирования | 0 | 1 | 2 | 3 | 4 |
| Процент получивших оценку | 3 | 24 | 40 | 26 | 7 |
Эти результаты можно представить в графическом виде. Такой способ представления называется гистограммой (Histogram) (рис. 2.1.2(5)а).
Упражнение 2.1.2(6). Пусть мы опросили 100 случайно выбранных граждан России. Что можно было бы назвать гистограммой распределения результатов тестирования тревожности по этой выборке?
Упражнение 2.1.2(7). Насколько гистограмма по выборке была бы похожа на гистограмму распределения результатов у всех граждан РФ?
Ответ на первый вопрос понятен. Надо вычислить проценты получивших те или иные баллы по тесту, нарисовать прямоугольники соответствующей величины и добавить соответствующие надписи.
Второй вопрос гораздо интереснее. Возможность статистической оценки параметров опирается на тот факт, что чаще всего выборочная гистограмма будет похожа на гистограмму по генеральной совокупности. На рис. 2.1.2(5)б, 2.1.2(5)в и 2.1.2(5)г приводятся три результата компьютерного моделирования гистограмм выборок по 100 человек из 100 000 000, имеющих процентное распределение оценок тревожности, отображенное на гистограмме (см. рис. 2.1.2(5)а).
Рис. 2.1.2(5) Гистограмма распределения результатов тестирования тревожности (а) у всех граждан РФ, (б), (в) и (г) — в случайных выборках объема 100 индивидов (в процентах).
Фундаментальный постулат, который хорошо согласуется с опытом, определяет наше отношение к данному сходству: наблюдаемые частоты при увеличении количества испытаний стремятся к частотам в генеральной совокупности. В случае испытаний тревожности граждан РФ постулат можно конкретизировать так: мы видим, что 3% генеральной совокупности характеризуются нулевой оценкой тревожности; если брать все увеличивающиеся выборки из данной генеральной совокупности, то процент минимально тревожных людей в них будет все ближе подходить к этим 3%.
Обычно мы не знаем распределение интересующего нас показателя у всех граждан России, и узнать его точный вид можем, только если проделаем огромную и дорогостоящую работу. Однако если выборочные гистограммы в каком-то смысле похожи на гистограммы распределения по всей генеральной совокупности, то ведь верно и обратное: если мы знаем выборочное распределение, то распределение генеральной совокупности должно быть на него похоже. Чтобы делать выводы о генеральной совокупности на основании выборок, мы должны научиться как-то оценивать «степень возможной похожести».
Пример 2.1.2(8). Предположим, нам надо выяснить, кто показывает более высокий балл по нашему тесту тревожности — мужчины или женщины. Выбрав случайно 50 мужчин и 50 женщин, мы просим их заполнить опросник и убеждаемся, что средний балл мужчин 2.4, в то время как у женщин средний балл 2.2. Мы можем надеяться, что выборочные значения похожи на средние по соответствующим частям генеральной совокупности. Однако не может ли быть, что нам случайно попались женщины спокойные, а мужчины столь же случайно попались очень тревожные, что и обусловило полученный результат?
Мы никогда не застрахованы полностью от принятия ошибочных решений, если опираемся на эмпирические данные, хотя бы часть вариации которых обеспечивается случайностью. Но в таких случаях мы можем оценивать надежность нашего вывода благодаря знанию того, как эта случайность может «себя вести» при многократных испытаниях.
Сделать это можно, изучая ситуации «хорошо организованных случайностей». Это случайности, о которых мы точно знаем нечто очень важное — вероятности событий, а другие важные вещи можем уверенно вывести средствами математики. Таким образом мы узнаем, насколько выборочные характеристики должны быть похожи на характеристики генеральных совокупностей, и сможем судить о вторых на основании первых. Сверх того, мы получим возможность решать разнообразные задачи, не сводимые к генеральным совокупностям, об этом речь пойдет ниже.
2.1.3. Случайность и вероятность
Говоря о случайном выборе из генеральной совокупности, мы использовали обыденное представление о равной возможности исходов некоторого испытания. Например, раскрутив барабан с написанными на нем именами, мы ожидаем, что у этих имен одинаковые шансы быть выбранными.
Классическое определение вероятности использует именно это представление. В простейшем случае двух равновероятных исходов какого-то заранее не определенного события вероятность каждого исхода считают равной 50 процентам. В теории вероятностей обычно не пользуются процентами, а выражают вероятность дробями или десятичными числами от 0 (невозможное событие) до 1 (достоверное событие)[2]. Например, для игральной кости вероятность каждого из 6 равновероятных результатов будет равна 1/6. В виде формулы это записывается так: \( p(1)=p(2)=p(3)=p(4)=p(5)=p(6)=1/6 \) (вероятность выпадения единицы равна вероятности выпадение двойки… равна 1/6). Латинская буква p для обозначения вероятностей предпочитается примерно так же, как буква x в алгебраических уравнениях. Так же, как в алгебре, могут использоваться и другие буквы.
Если нас интересует вероятность сложного события, например, выпадения на игральной кости четного числа, то поскольку три простых равновероятных исхода соответствуют этому сложному событию (выпадение 2, 4 и 6), то и вероятность его вычисляется: \( p(2 \cup 4 \cup 6)=1/6+1/6+1/6=3/6=1/2 \).
Пусть имеется некоторое множество равновозможных исходов какого-то испытания. Пусть некоторые из них выделены как предпочтительные в каком-то смысле (например, при игре в рулетку мы поставили рубль «на красное»), и нас интересует событие «выпадает один из предпочтительных исходов» (т.е. в нашем примере шарик остановился на красной цифре). Тогда вероятность этого события равна отношению числа предпочтительных исходов к общему числу равновероятных исходов (в нашем примере число красных клеток рулетки 18, всего же имеется 37 клеток, следовательно, вероятность выиграть равна 18/37). Это так называемое классическое определение вероятности.
Для такой случайности и связанных с ней представлений о вероятности можно сформулировать свой вариант постулата о частотах: если мы имеем несколько равновероятных исходов какого-то испытания, которое можно повторять неограниченно, то при увеличении количества испытаний частоты появления всех исходов будут стремиться к равенству. Этот постулат является всего лишь уточнением практической интуиции, которой обладают люди до всякого знакомства с теорией вероятностей и статистикой.
Если монету изогнуть или опилить до формы усеченного конуса, она перестанет быть симметричной, и говорить о равных шансах выпадения герба и цифры становится невозможно. Можем ли мы в этом случае считать, что какие-то вероятности все же могут быть приписаны этим возможным событиям — выпадению герба и цифры? Математики считают — да, хотя теоретически рассчитать эти вероятности невозможно. Сформулированный выше постулат относится и к этому случаю: если проводить все более длинные серии подбрасываний подпиленной монеты, то частоты выпадения герба будут сходиться к этой неизвестной вероятности. Таким образом, неизвестные вероятности можно оценивать с помощью длинных серий испытаний.
2.1.4. Выборки и выборочные распределения.
Что будет, если мы подбросим сразу две одинаковые монеты? В результате такого опыта на столе могут оказаться две цифры, цифра и герб либо два герба. Вероятности этих результатов отображаются диаграммой, в которой столбцы подписаны нулем, единицей и двойкой — количеством выпавших гербов (рис. 2.1.4(1)а). Возможны четыре равновероятных исхода: «герб, герб», «цифра, герб», «герб, цифра» и «цифра, цифра» Результат «при двух бросках монеты выпал один герб» является суммой результатов двух из них («герб, цифра» и «цифра, герб»), поэтому соответствующая вероятность равна 1/4+1/4=1/2.
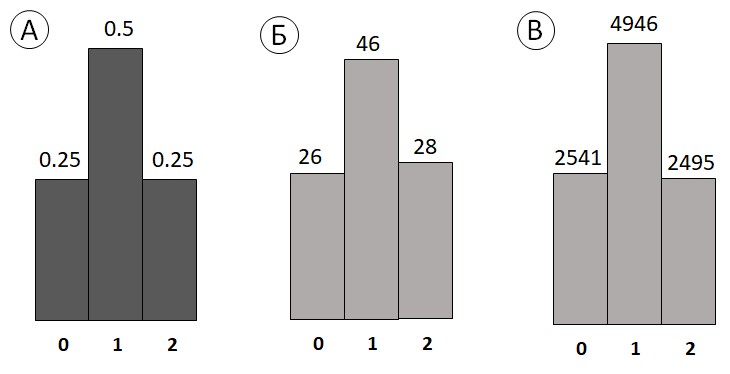Рис 2.1.4(1) Диаграмма распределения вероятностей количества выпавших гербов при двукратном подбрасывании монеты (а), гистограмма частот количества выпавших гербов при 100 испытаниях (б) и при 10000 испытаниях (в) двукратного подбрасывания монеты.
Результаты испытаний похожи на теоретические диаграммы, причем можно сказать, что распределение вероятностей как бы «притягивает» частоты при увеличении числа испытаний. На рис. 2.1.4(1)б приведена гистограмма выборочного распределения результатов 100 подбрасываний пары монет. На рис. 2.1.4(1)в аналогичная гистограмма, полученная по результатам 10 000 подбрасываний[3]. Легко заметить, что вторая гистограмма почти не отличается от диаграммы теоретического распределения.
Замечание. Мы будем всегда использовать слово «диаграмма» для изображений теоретического распределения и «гистограмма» — для выборочного распределения.
>> следующий параграф>>
[1] Иногда для простоты изложения мы будем называть генеральной совокупностью само множество индивидов, а не множество значений интересующей нас характеристики.
[2] Теория, правда, делает оговорки — в некоторых теоретических моделях могут наступать события, имеющие нулевую вероятность (см. параграф 3.1.5).
[3] Мы не подбрасывали настоящие монеты, а смоделировали процесс на компьютере.