3.3.1. Практикум по случайным величинам в SPSS
Пример 3.3(1) Рассмотрим пример, иллюстрирующий смысл выборочного среднего на материале ситуации азартной игры. Допустим, нам предлагают сыграть на игральном автомате, причем одна игра стоит 5 рублей. Выигрыш может составлять 0, 10, 100 и 1000 рублей. Нам точно не известен закон, по которому распределяются выигрыши, но из надежных источников мы получили их статистику. Данные о результатах 1000 игр содержатся в файле Play.sav в переменной profit. Имея эти данные, мы можем оценить, насколько выгодно играть в такую игру. Для этого рассчитаем выборочное среднее по имеющимся у нас данным. Для этого в SPSS надо зайти в меню Анализ — Описательные статистики — Описательные (Analyze — Descriptive statistics — Descriptives). В диалоговом окне в поле Переменные (Variable(s)) перенесем переменную profit. После нажатия кнопки OK в окне вывода появится таблица.
Таблица 3.3.1(2). Описательная статистика выигрышей
| Описательные статистики | |||||
| N | Минимум | Максимум | Среднее | Среднекв. отклонение |
|
| Profit | 1 000 | .00 | 1 000.00 | 6.3600 | 35.58675 |
| N валидных (по списку) | 1 000 | ||||
В столбце «Среднее» находится интересующее нас число — выборочная оценка математического ожидания — в среднем за игру мы будем получать 6.36 рубля, т.е. при достаточно долгой игре, платя за каждую попытку 5 рублей, в среднем мы будем выигрывать 1.36 рубля. Нам эта игра выгодна.
Замечание. Мы не должны забывать, что выборочная оценка не совпадает с истинным математическим ожиданием. Однако в практических случаях мы можем использовать наши оценки, считая их удовлетворительно точными (чем больше выборка, тем точнее). Об оценках точности оценок см. главу 5.
Упражнение 3.3(3). Выведите таблицу частот выигрышей по данной выборке (Описательные статистики — Частоты (Descriptive statistics — Frequences); затем перенести имя profit в поле Переменные (Variables)). Рассматривая частоты как оценки вероятностей, подставьте полученные значения в формулу математического ожидания вместе с величинами соответствующих выигрышей. Убедитесь, что полученный результат совпадает с выведенным средним в предыдущей таблице, равным 6.36.
Пример 3.3(4). Обратимся теперь к использованию оценок математического ожидания и дисперсии случайной величины в рамках простого психологического исследования. Допустим, мы исследуем состояние так называемых управляющих функций у учащихся двух школ: обычной и инклюзивной. Мы измеряем состояние этих функций с помощью нейропсихологического обследования, в рамках которого ребенку дается ряд заданий, оценивающих функции произвольной регуляции деятельности. На основании их выполнения высчитывается интегральный показатель состояния интересующих нас функций. Этот полученный балл для конкретного человека, разумеется, не случаен — он зависит от уровня развития когнитивной сферы, созревания соответствующих мозговых структур и множества других факторов. Однако мы можем предполагать, что две группы наших испытуемых — дети из обычной школы и дети из инклюзивной школы — это случайные выборки из двух разных генеральных совокупностей, которые характеризуются, возможно, разными средними значениями и дисперсиями. Если связать каждую из генеральных совокупностей со случайной величиной, реализующейся случайным выбором представителя из данной совокупности, то наши выборки являются реализациями испытаний этих случайных величин, а мы оцениваем их параметры.
В файле Executive.sav приведены модельные данные такого исследования. В первом столбце index_exec содержатся интегральные оценки управляющих функций 50 детей-первоклассников, 25 из которых учатся в обычной школе, и еще 25 — в инклюзивной школе. Переменная index_exec содержит штрафные баллы при выполнении заданий, поэтому низкие оценки соответствуют хорошему состоянию функций, а высокие — плохому. Принадлежность ученика к школе закодирована переменной school: 1 — учащийся обычной школы, 2 — учащийся инклюзивной школы.
Рассчитаем среднее и дисперсию в двух выборках. Чтобы сделать это отдельно для двух групп испытуемых в SPSS, можно зайти в меню Анализ — Сравнение средних — Средние (Analyze — Compare Means — Means). В диалоговом окне в поле Список зависимых переменных (Dependent List) перенесем оцениваемую переменную index_exec, а в поле Список независимых переменных (Independent List) — переменную school. Далее, в дополнительном меню Параметры (Options) перенесем в поле Статистики в ячейках (Cell Statistics) из полного списка возможных параметров Дисперсию (Variance). Закроем это окно и запустим анализ (кнопка OK). В результате будет получена таблица.
Таблица 2.3(5) Таблица средних по группам.
| Отчет | |||
| index of executive functions | |||
| school | Среднее | N | Стандартная отклонения |
| regular school | -.0749 | 25 | 1.05820 |
| inclusive school | .0520 | 25 | 3.31392 |
| Всего | -.0114 | 50 | 2.43547 |
Из таблицы видно, что выборочные средние в двух группах различаются незначительно (-0.075 и 0.052 в обычной и инклюзивной школе, соответственно). Мы можем надеяться, что реальные математические ожидания случайных величин «индекс управляющих функций учащегося обычной школы» и «индекс управляющих функций учащегося инклюзивной школы» также мало отличаются друг от друга. С другой стороны, дисперсии в двух выборках отличаются очень сильно: 1.03 и 10.982 в обычной и инклюзивной школах соответственно.
Для прояснения ситуации полезно построить гистограммы для двух выборок: Графика — Устаревшие диалоговые окна — Гистограмма (Graphics — Legacy Dialogs — Histogram). Чтобы построить два отдельных графика для каждой выборки, в поле Строки (Rows) следует перенести переменную school. Получившаяся гистограмма приведена на рисунке 3.3(5).
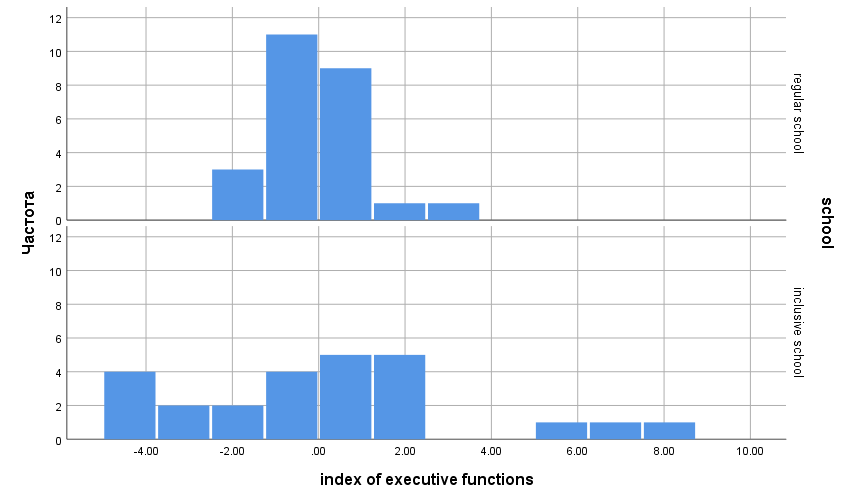Рис. 3.3(5). Гистограмма распределения индекса управляющих функций для обычной и инклюзивной школ
На графиках отчетливо видно, что в обычной школе почти все дети получили баллы, близкие к среднему (-0.075), а в инклюзивной школе при практически таком же среднем разброс данных намного больше. Таким образом, в этом примере различия между выборками проявились не в среднем, а в дисперсии. Мы можем думать, что выборочные оценки отражают характеристики генеральных совокупностей (и связанных с ними случайных величин).
Содержательно различие дисперсий объясняется тем, что в инклюзивной школе состав учеников более разнороден по сравнению с обычной школой, что вполне объяснимо: в инклюзивной школе дети с нарушениями в развитии могут демонстрировать дефицит различных когнитивных функций, а управляющие функции могут быть у них не только не нарушены, но и хорошо развиты — помогая (компенсаторно) справляться с другими трудностями.
Пример 3.3(6). Стандартизация переменных.
В некоторой незадачливой стране перевод школьного образования на единый экзамен происходит поэтапно. В 2016 году знания по математике оценивались традиционно, по пятибалльной шкале, а по русскому языку проводился ЕГЭ, оценивавшийся по стобалльной шкале. На факультете психологии столичного университета школьников принимают по результатам этих двух дисциплин, суммируя оценки.
Вопрос 3.3(7). Какой из предметов окажет большее влияние на суммарный балл в этом университете?
В файле EgeSum.sav содержатся модельные данные результатов 100 школьников. В переменной Math приведены оценки по математике (в шкале от 1 до 5), а в переменной Rus — по русскому зыку (в шкале от 1 до 100).
Упражнение 3.3(8). Вычислите переменную Sum = Math + Rus. Произведите сортировку школьников по переменной Sum (Данные — Сортировать наблюдения (Data — Sort cases), затем перенесите имя Sum в поле Переменные (Variables)).
Убедитесь, что среди лучших двадцати есть несколько школьников, получивших по математике два и три. Таким образом, оценка по русскому языку дает больший вклад.
Есть универсальный способ сделать вклад дисциплин равным — провести стандартизацию данных. Тогда сырые значения окажутся приведены к единому масштабу — со средним значением 0 и дисперсией равной 1. Рассчитаем сначала среднее и стандартное отклонение для двух переменных (Анализ — Описательные статистики — Описательные (Analysis — Descriptive Statistics — Descriptives)). Результат представлен в таблице.
Таблица 3.3(9). Описательная статистика исходных оценок по ЕГЭ.
| Описательные статистики | |||||
| N | Минимум | Максимум | Среднее | Стд. отклонение | |
| Math | 100 | 2.00 | 5.00 | 4.1500 | .85723 |
| Rus | 100 | 61.00 | 86.00 | 74.3400 | 4.68874 |
| N валидных (целиком) | 100 | ||||
Из таблицы видно, что стандартные отклонения двух переменных значительно отличаются и поэтому суммирование и привело к большему влиянию переменной Rus с бóльшим стандартным отклонением. Для того чтобы можно было объединить две оценки, мы стандартизуем обе переменные, т.е. вычтем из значений каждой переменной ее среднее и поделим на ее стандартное отклонение. Деление на стандартное отклонение придаст слагаемым одинаковый масштаб (стандартное отклонение станет равно единице). Сначала стандартизуем переменную Math. Среднее по ней составляет 4.15, стандартное отклонение — примерно 0.86. Выберем в меню пункты Преобразовать — Вычислить (Transform — Compute). В открывшемся окне в строке Вычисляемая переменная (Target variable) слева сверху введем название, которые мы хотим дать новой, стандартизованной переменной — MathSt. Далее справа сверху нам нужно вписать формулу для расчета этой переменной, а именно (Math — 4.15 )/0.86. Нажатие кнопки ОК приведет к появлению нового столбца в файле с данными — стандартизованных значений. Если теперь мы рассчитаем среднее и стандартное отклонение новой переменной MathSt (так же, как описано выше — при помощи описательной статистики), среднее составит 0, а стандартное отклонение 0.99. Тот факт, что стандартное отклонение у нас получилось приблизительно, а не точно, равным единице, объясняется просто: тем, что мы делили на округленное стандартное отклонение.
Вторую переменную Rus мы можем стандартизовать тем же способом. Однако существует и более простой путь: в знакомом нам окне расчета описательных статистик (Анализ — Описательные статистики — Описательные, Analysis — Descriptive Statistics — Descriptives), перенесем в поле Переменные (Variables) те переменные, которые хотим стандартизовать (Math и Rus) и отметим внизу галочкой пункт Сохранить стандартизованные значения в переменных (Save standardized values as variables). После нажатия ОК в таблице данных появятся две колонки: ZMath — стандартизованные значения переменной Math и ZRus — стандартизованные значения переменной Rus. Можно заметить, что значения испытуемых по рассчитанной нами переменной Math.st и рассчитанной компьютером переменной ZMath очень похожи и различаются только из-за того, что мы округлили значения стандартного отклонения.
Рассчитаем средние и стандартные отклонения новых стандартизованных переменных (выберем Анализ — Описательные статистики — Описательные и введем в поле Переменные ZMath и ZRus). Результаты представлены в таблице 3.3(10) Как видим, теперь средние равны 0, а стандартные отклонения 1 — мы привели переменные к единой шкале.
Таблица 3.3(10). Описательная статистика стандартизированных переменных.
| Описательные статистики | |||||
| N | Минимум | Максимум | Среднее | Среднекв. отклонение | |
| Zscore(Math) | 100 | -2.50807 | .99156 | 0.0000000 | 1.00000000 |
| Zscore(Rus) | 100 | -2.84512 | 2.48681 | 0.0000000 | 1.00000000 |
| N валидных (по списку) | 100 | ||||
Теперь, после такого преобразования, мы можем рассчитать итоговый суммарный балл по двум предметам. Используя знакомую процедуру вычисления переменной, вычислим новую переменную, сложив переменные ZMath и ZRus, назваем ее SumZ.
Вопрос 3.3(11). Чему будет равно среднее новой переменной?
Упражнение 3.3(12). Произведите ранжирование по переменным Sum и SumZ (Преобразовать — Ранжировать наблюдения (Transform — Range cases)). В поле переменных можно перенести обе переменных разом. Убедитесь, что ранги не совпадают.
Упорядочите наблюдения по переменной SumZ. Убедитесь, что среди лучших двадцати процентов присутствуют абитуриенты лишь с верхними оценками по русскому языку и математике.
3.3.2. Практикум по случайным величинам в Jamovi
Пример 3.3(1)j Рассмотрим пример, иллюстрирующий смысл выборочного среднего на материале ситуации азартной игры. Допустим, нам предлагают сыграть на игральном автомате, причем одна игра стоит 5 рублей. Выигрыш может составлять 0, 10, 100 и 1000 рублей. Нам точно не известен закон, по которому распределяются выигрыши, но из надежных источников мы получили их статистику. Данные о результатах 1000 игр содержатся в файле Play.sav в переменной profit1. Имея эти данные, мы можем оценить, насколько выгодно играть в такую игру. Для этого рассчитаем выборочное среднее по имеющимся у нас данным. Для этого в Jamovi надо зайти в меню Analyses —Exploration — Descriptives. В диалоговом окне в поле Variables перенесем переменную profit1.В окне вывода появится таблица.
Таблица 3.3(2)j. Описательная статистика выигрышей
| Descriptives | |||
| profit1 | |||
| N | 1000 | ||
| Missing | 0 | ||
| Mean | 6.36 | ||
| Median | 0.00 | ||
| Minimum | 0 | ||
| Maximum | 1000 | ||
В строке Mean находится интересующее нас число — выборочная оценка математического ожидания — в среднем за игру мы будем получать 6.36 рубля, т.е. при достаточно долгой игре, платя за каждую попытку 5 рублей, в среднем мы будем выигрывать 1.36 рубля. Нам эта игра выгодна.
Замечание. Мы не должны забывать, что выборочная оценка не совпадает с истинным математическим ожиданием. Однако в практических случаях мы можем использовать наши оценки, считая их удовлетворительно точными (чем больше выборка, тем точнее). Об оценках точности оценок см. главу 5.
Упражнение 3.3(3)j. Выведите таблицу частот выигрышей по данной выборке (Поставьте галочку в окошко Frequency tables). Интересующий нас результат в столбце % of Total. Надо иметь в виду, что частоты получаются из процентов делением на 100. Рассматривая частоты как оценки вероятностей, подставьте полученные значения в формулу математического ожидания вместе с величинами соответствующих выигрышей. Убедитесь, что полученный результат совпадает с выведенным средним в предыдущей таблице, равным 6.36.
Пример 3.3(4)j. Обратимся теперь к использованию оценок математического ожидания и дисперсии случайной величины в рамках простого психологического исследования. Допустим, мы исследуем состояние так называемых управляющих функций у учащихся двух школ: обычной и инклюзивной. Мы измеряем состояние этих функций с помощью нейропсихологического обследования, в рамках которого ребенку дается ряд заданий, оценивающих функции произвольной регуляции деятельности. На основании их выполнения высчитывается интегральный показатель состояния интересующих нас функций. Этот полученный балл для конкретного человека, разумеется, не случаен — он зависит от уровня развития когнитивной сферы, созревания соответствующих мозговых структур и множества других факторов. Однако мы можем предполагать, что две группы наших испытуемых — дети из обычной школы и дети из инклюзивной школы — это случайные выборки из двух разных генеральных совокупностей, которые характеризуются, возможно, разными средними значениями и дисперсиями. Если связать каждую из генеральных совокупностей со случайной величиной, реализующейся случайным выбором представителя из данной совокупности, то наши выборки являются реализациями испытаний этих случайных величин, а мы оцениваем их параметры.
В файле Executive.sav приведены модельные данные такого исследования. В первом столбце exec_index содержатся интегральные оценки управляющих функций 50 детей-первоклассников, 25 из которых учатся в обычной школе, и еще 25 — в инклюзивной школе. Переменная exec_index содержит штрафные баллы при выполнении заданий, поэтому низкие оценки соответствуют хорошему состоянию функций, а высокие — плохому. Принадлежность ученика к школе закодирована переменной school: 1 — учащийся обычной школы, 2 — учащийся инклюзивной школы.
Рассчитаем среднее и дисперсию в двух выборках. Чтобы сделать это отдельно для двух групп испытуемых в Jamovi можно зайти в меню Analyses — Exploration — Descriptives. В диалоговом окне в поле Variables перенесем оцениваемую переменную exec_index, а в поле Split by — переменную school. Затем, чтобы не выводить лишнюю информацию, в разделе Statistics можно отключить пункты Missing (информацию о пропущенных данных), Median (медианы в группах нас в данный момент не интересуют), Minimum и Maximum. В результате будет получена следующая таблица
Таблица 3.3(5) Таблица средних по группам.
| Descriptives | |||||
| school | exec_index | ||||
| N | regular school | 25 | |||
| inclusive school | 25 | ||||
| Mean | regular school | -0.0749 | |||
| inclusive school | 0.0520 | ||||
В полученной таблице нас интересует пара строк Mean. Из таблицы видно, что выборочные средние в двух группах различаются незначительно (-0.0749 и 0.0520) в обычной и инклюзивной школе, соответственно). Мы можем надеяться, что реальные математические ожидания случайных величин «индекс управляющих функций учащегося обычной школы» и «индекс управляющих функций учащегося инклюзивной школы» также мало отличаются друг от друга. Можно вывести стандартные отклонения (для этого в панели опций поставьте галочки в пункте Std. Deviation) и увидеть, что в двух выборках они отличаются очень сильно: 1.06 и 3.31 в обычной и инклюзивной школах соответственно.
Для прояснения ситуации полезно построить гистограммы для двух выборок: в конце панели опций нажмите на вкладку Plots и поставьте галочку в окно Histogram. Получившиеся гистограммы приведены на рисунке 3.3(6)j.
Рис. 3.3(6)j. Гистограмма распределения индекса управляющих функций для обычной и инклюзивной школ
На графиках отчетливо видно, что в обычной школе почти все дети получили баллы, близкие к среднему (около нуля), а в инклюзивной школе при практически таком же среднем разброс данных намного больше. Таким образом, в этом примере различия между выборками проявились не в среднем, а в дисперсии. Мы можем думать, что выборочные оценки отражают характеристики генеральных совокупностей (и связанных с ними случайных величин).
Содержательно различие дисперсий объясняется тем, что в инклюзивной школе состав учеников более разнороден по сравнению с обычной школой, что вполне объяснимо: в инклюзивной школе дети с нарушениями в развитии могут демонстрировать дефицит различных когнитивных функций, а управляющие функции могут быть у них не только не нарушены, но и хорошо развиты — помогая (компенсаторно) справляться с другими трудностями.
Пример 3.3(7)j. Стандартизация переменных.
В некоторой незадачливой стране перевод школьного образования на единый экзамен происходит поэтапно. В 2016 году знания по математике оценивались традиционно, по пятибалльной шкале, а по русскому языку проводился ЕГЭ, оценивавшийся по стобалльной шкале. На факультете психологии столичного университета школьников принимают по результатам этих двух дисциплин, суммируя оценки.
Вопрос 3.3(8)j. Какой из предметов окажет большее влияние на суммарный балл в этом университете?
В файле EgeSum.sav содержатся модельные данные результатов 100 школьников. В переменной Math приведены оценки по математике (в шкале от 1 до 5), а в переменной Rus — по русскому зыку (в шкале от 1 до 100).
Упражнение 3.3(9). Вычислите переменную Sum = Math + Rus. Для этого выберите пункты Data – Compute и впишите имя Sum в верхнее окно, а выражение Math + Rus в правое нижнее.
Убедитесь, что среди лучших двадцати есть несколько школьников, получивших по математике два и три. Таким образом, оценка по русскому языку дает больший вклад.
Есть универсальный способ сделать вклад дисциплин равным — провести стандартизацию данных. Тогда сырые значения окажутся приведены к единому масштабу — со средним значением 0 и дисперсией равной 1. Рассчитаем сначала среднее и стандартное отклонение для двух переменных (Analyses — Exploration — Descriptives и перенесем переменные в окно Variables). Затем снимем ненужные нам пункты Missing, Median, Minimum и Maximum, включим галочку в пункте Std. deviation. Результат представлен в таблице.
Таблица 3.3(10)j. Описательная статистика исходных оценок по ЕГЭ.
| Descriptives | |||||
| Math | Rus | ||||
| N | 100 | 100 | |||
| Mean | 4.1500 | 74.3400 | |||
| Standard deviation | 0.8572 | 4.6887 | |||
Из таблицы видно, что стандартные отклонения двух переменных значительно отличаются и поэтому суммирование и привело к большему влиянию переменной Rus с бóльшим стандартным отклонением. Для того чтобы можно было объединить две оценки, мы стандартизуем обе переменные, т.е. вычтем из значений каждой переменной ее среднее и поделим на ее стандартное отклонение. Деление на стандартное отклонение придаст слагаемым одинаковый масштаб (стандартное отклонение станет равно единице). Сначала стандартизуем переменную Math. Среднее по ней составляет 4.15, стандартное отклонение — примерно 0.86. Выберем в меню пункты Data – Compute и проведем операцию аналогично предыдущему вычислению суммы. В верхнее окно впишем MathSt, а в правое нижнее (Math — 4.15) / 0.86. Нажатие кнопки ОК приведет к появлению нового столбца в файле с данными — стандартизованных значений. Если теперь мы рассчитаем среднее и стандартное отклонение новой переменной MathSt (так же, как описано выше — при помощи описательной статистики), среднее составит 0, а стандартное отклонение 0.99. Тот факт, что стандартное отклонение у нас получилось приблизительно, а не точно, равным единице, объясняется просто: тем, что мы делили на округленное стандартное отклонение.
Вторую переменную Rus мы можем стандартизовать тем же способом и получить RusSt = (Rus – 74.3) / 4.7. Рассчитаем средние и стандартные отклонения новых стандартизованных переменных (Analyses — Exploration — Descriptives и перенесем переменные MathSt и RusSt в окно Variables). Результаты представлены в таблице 3.3(10)j Как видим, теперь средние близки к нулю, а стандартные отклонения к единиице — мы привели переменные к единой шкале.
Таблица 3.3(11)j. Описательная статистика стандартизированных переменных.
| Descriptives | |||||
| MathSt | RusSt | ||||
| N | 100 | 100 | |||
| Mean | -3.86e−16 | 0.00851 | |||
| Standard deviation | 0.997 | 0.998 | |||
Теперь, после такого преобразования, мы можем рассчитать итоговый суммарный балл по двум предметам. Используя знакомую процедуру вычисления переменной, вычислим новую переменную, сложив переменные MathSt и RusSt, назваем ее SumSt.
Вопрос 3.3(12)j. Чему будет равно среднее новой переменной?
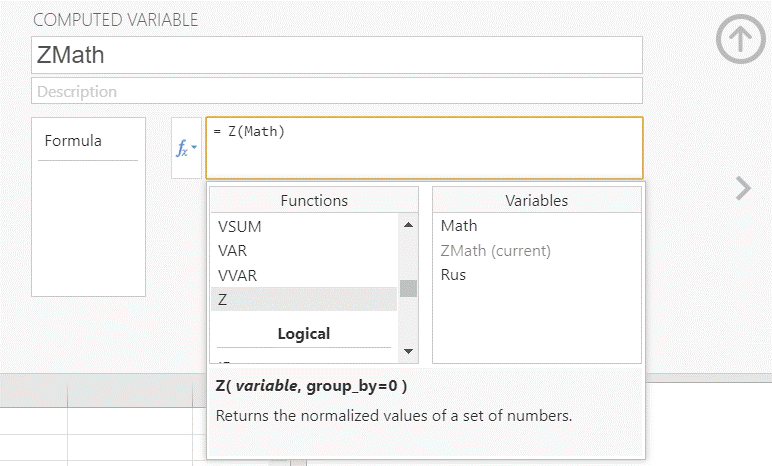
Примечание: достаточно часто используемую при анализе процедуру стандартизации (которая также называется z-преобразованием) в Jamovi также можно проводить с помощью встроенной функции Z. Для этого надо зайти в меню Data – Compute, затем ввести имя новой переменной (например, ZMath), затем в списке функций в разделе Statistical найти функцию Z и в качестве аргумента ввести имя стандартизуемой переменной Math (см. рис. 3.3(13)j. После этого будет рассчитана новая переменная. Убедитесь, что она будет совпадать с переменной MathSt с точностью до округления.
Рис. 3.3(13)jj. Пример расчет стандартизированной переменной в Jamovi
Упражнение 3.3(14)j. Убедитесь, что среди лучших двадцати процентов по переменной SumSt присутствуют абитуриенты лишь с верхними оценками по русскому языку и математике.
3.3.3. Практикум по случайным величинам в Rstudio
Пример 3.3(1)r Рассмотрим пример, иллюстрирующий смысл выборочного среднего на материале ситуации азартной игры. Допустим, нам предлагают сыграть на игральном автомате, причем одна игра стоит 5 рублей. Выигрыш может составлять 0, 10, 100 и 1000 рублей. Нам точно не известен закон, по которому распределяются выигрыши, но из надежных источников мы получили их статистику. Данные о результатах 1000 игр содержатся в файле Play.sav в переменной profit. Имея эти данные, мы можем оценить, насколько выгодно играть в такую игру. Для этого загрузим данные в таблицу data_game и рассчитаем выборочное среднее по имеющимся у нас данным. Для этого можно использовать функцию mean:
data_game <- read.spss("Play.sav", to.data.frame = T, reencode = "utf8")
mean(data_game$profit1)
Как видно из результата среднее (выборочная оценка математического ожидания) равна 6.36, то есть можно сказать, что в среднем за игру мы будем получать 6.36 рубля. Таким образом, при достаточно долгой игре, платя за каждую попытку 5 рублей, в среднем мы будем выигрывать 1.36 рубля. Нам эта игра выгодна.
Замечание. Мы не должны забывать, что выборочная оценка не совпадает с истинным математическим ожиданием. Однако в практических случаях мы можем использовать наши оценки, считая их удовлетворительно точными (чем больше выборка, тем точнее). Об оценках точности оценок см. главу 5.
Упражнение 3.3(2)r. Выведите таблицу относительных частот выигрышей по данной выборке с помощью функций table и prop.table (см. пример 2.3(1)r). Рассматривая частоты как оценки вероятностей, подставьте полученные значения в формулу математического ожидания вместе с величинами соответствующих выигрышей. Убедитесь, что полученный результат совпадает с выведенным средним в предыдущей таблице, равным 6.36.
Пример 3.3(3)r. Обратимся теперь к использованию оценок математического ожидания и дисперсии случайной величины в рамках простого психологического исследования. Допустим, мы исследуем состояние так называемых управляющих функций у учащихся двух школ: обычной и инклюзивной. Мы измеряем состояние этих функций с помощью нейропсихологического обследования, в рамках которого ребенку дается ряд заданий, оценивающих функции произвольной регуляции деятельности. На основании их выполнения высчитывается интегральный показатель состояния интересующих нас функций. Этот полученный балл для конкретного человека, разумеется, не случаен — он зависит от уровня развития когнитивной сферы, созревания соответствующих мозговых структур и множества других факторов. Однако мы можем предполагать, что две группы наших испытуемых — дети из обычной школы и дети из инклюзивной школы — это случайные выборки из двух разных генеральных совокупностей, которые характеризуются, возможно, разными средними значениями и дисперсиями. Если связать каждую из генеральных совокупностей со случайной величиной, реализующейся случайным выбором представителя из данной совокупности, то наши выборки являются реализациями испытаний этих случайных величин, а мы оцениваем их параметры.
В файле Executive.sav приведены модельные данные такого исследования. В первом столбце index_exec содержатся интегральные оценки управляющих функций 50 детей-первоклассников, 25 из которых учатся в обычной школе, и еще 25 — в инклюзивной школе. Переменная index_exec содержит штрафные баллы при выполнении заданий, поэтому низкие оценки соответствуют хорошему состоянию функций, а высокие — плохому. Принадлежность ученика к школе закодирована переменной school: 1 — учащийся обычной школы, 2 — учащийся инклюзивной школы.
Загрузим данные в таблицу data_exec и рассчитаем среднее и дисперсию в двух выборках. Чтобы сделать это отдельно для двух групп испытуемых можно использовать функцию aggregate, которая рассчитывает любую функцию от дельно для групп по указанной формуле x ~ y, где x – анализируемая переменная, а y – группирующая:
data_exec <- read.spss("Executive.sav", to.data.frame = T, reencode = "utf8")
aggregate(exec_index ~ school, data_exec, mean)
aggregate(exec_index ~ school, data_exec, var)
В результате выполнения этих команд получим следующий результат в консоли:
> aggregate(exec_index ~ school, data_exec, mean) school exec_index 1 обычная школа -0.07490352 2 инклюзивная школа 0.05201123 > aggregate(exec_index ~ school, data_exec, var) school exec_index 1 обычная школа 1.119788 2 инклюзивная школа 10.982043
Из таблицы видно, что выборочные средние в двух группах различаются незначительно (-0.075 и 0.052 в обычной и инклюзивной школе, соответственно). Мы можем надеяться, что реальные математические ожидания случайных величин «индекс управляющих функций учащегося обычной школы» и «индекс управляющих функций учащегося инклюзивной школы» также мало отличаются друг от друга. С другой стороны, дисперсии в двух выборках отличаются очень сильно: 1.119 и 10.982 в обычной и инклюзивной школах соответственно.
Для прояснения ситуации полезно построить гистограммы для двух выборок. Так как в данном примере анализируемая переменная числовая, то в данном случае можно использовать стандартную функцию hist. Так как нам необходимо вывести распределения отдельно для двух групп можно выполнить команду два раза, подавая в качестве данных строки, отобранные по условию принадлежности первой или второй группы:
hist(data_exec$exec_index[data_exec$school == "обычная школа"], xlim = c(-6, 10), main="Обычная школа", xlab="Управляющие функции") hist(data_exec$exec_index[data_exec$school == "инклюзивная школа"], xlim = c(-6, 10), , main="Инклюзивная школа", , xlab="Управляющие функции")
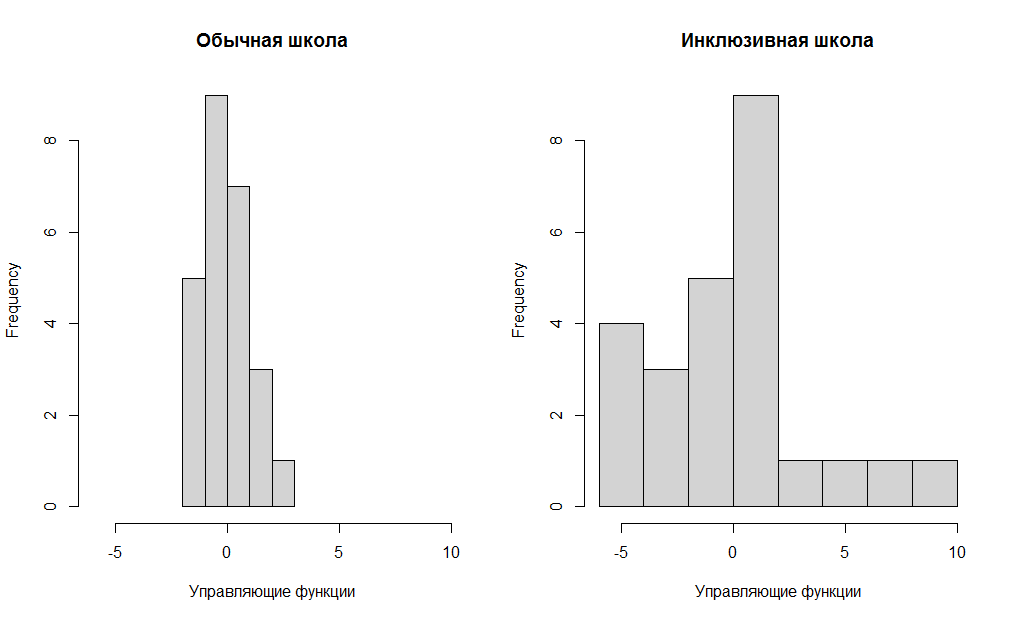
Для удобства сопоставления двух графиков мы выровняли интервал оси X (xlim – пределы оси Х от -6 до 10, эти значения подобраны эмпирически), а также задали понятный заголовок (main) и название оси X (xlab). В результате мы получили два графика, изображенных на рис. 3.3(4)r.
Рис. 3.3(4)r. Гистограмма распределения индекса управляющих функций для обычной и инклюзивной школ
На графиках отчетливо видно, что в обычной школе почти все дети получили баллы, близкие к среднему (-0.075), а в инклюзивной школе при практически таком же среднем разброс данных намного больше. Таким образом, в этом примере различия между выборками проявились не в среднем, а в дисперсии. Мы можем думать, что выборочные оценки отражают характеристики генеральных совокупностей (и связанных с ними случайных величин).
Содержательно различие дисперсий объясняется тем, что в инклюзивной школе состав учеников более разнороден по сравнению с обычной школой, что вполне объяснимо: в инклюзивной школе дети с нарушениями в развитии могут демонстрировать дефицит различных когнитивных функций, а управляющие функции могут быть у них не только не нарушены, но и хорошо развиты — помогая (компенсаторно) справляться с другими трудностями.
Пример 3.3(5)r. Стандартизация переменных.
В некоторой незадачливой стране перевод школьного образования на единый экзамен происходит поэтапно. В 2016 году знания по математике оценивались традиционно, по пятибалльной шкале, а по русскому языку проводился ЕГЭ, оценивавшийся по стобалльной шкале. На факультете психологии столичного университета школьников принимают по результатам этих двух дисциплин, суммируя оценки.
Вопрос 3.3(6)r. Какой из предметов окажет большее влияние на суммарный балл в этом университете?
В файле EgeSum.sav содержатся модельные данные результатов 100 школьников. В переменной Math приведены оценки по математике (в шкале от 1 до 5), а в переменной Rus — по русскому зыку (в шкале от 1 до 100).
Упражнение 3.3(7)r. Загрузив данные в таблицу, вычислите новую переменную Sum = Math + Rus. Произведите сортировку школьников по переменной Sum.
Убедитесь, что среди лучших двадцати есть несколько школьников, получивших по математике два и три. Это связано с тем, то в силу различий в шкалах, оценка по русскому языку дает больший вклад.
Есть универсальный способ сделать вклад дисциплин равным — провести стандартизацию данных. Тогда сырые значения окажутся приведены к единому масштабу — со средним значением 0 и дисперсией равной 1. Рассчитаем сначала среднее и стандартное отклонение для двух переменных:
library(psych)
data_ege <- read.spss("EgeSum.sav", to.data.frame = T, reencode = "utf8")
> describe(data_ege)
и получим следующий результат:
vars n mean sd median trimmed mad min max range skew kurtosis se Math 1 100 4.15 0.86 4 4.24 1.48 2 5 3 -0.67 -0.44 0.09 Rus 2 100 74.34 4.69 75 74.31 4.45 61 86 25 -0.01 -0.08 0.47
Из результата видно, что стандартные отклонения двух переменных значительно отличаются и поэтому суммирование и привело к большему влиянию переменной Rus с бóльшим стандартным отклонением. Для того чтобы можно было объединить две оценки, мы стандартизуем обе переменные, т.е. вычтем из значений каждой переменной ее среднее и поделим на ее стандартное отклонение. Деление на стандартное отклонение придаст слагаемым одинаковый масштаб (стандартное отклонение станет равно единице). Сначала стандартизуем переменную Math и запишем результат в переменную MathSt:
data_ege$ZMath <- (data_ege$Math - 4.15) / 0.86
Если теперь мы рассчитаем среднее и стандартное отклонение новой переменной ZMath (так же, как описано выше — при помощи функции describe), среднее составит 0, а стандартное отклонение 1.00. При более точном выводе результата может обнаружиться небольшое отклонения среднего и стандартного отклонения от этих значений, связанное с округлением.
Вторую переменную Rus мы можем стандартизовать тем же способом. Однако существует и более простой путь, в R стандартизация проводится автоматически с помощью функции scale. Назовём новую переменную ZRus:
data_ege$ZRus <- scale(data_ege$Rus)
Рассчитаем средние и стандартные отклонения новых стандартизованных переменных:
describe((data_ege[, c("ZMath", "ZRus")]))
vars n mean sd median trimmed mad min max range skew kurtosis se
ZMath 1 100 0 1 -0.17 0.10 1.72 -2.50 0.99 3.49 -0.67 -0.44 0.1
ZRus 2 100 0 1 0.14 -0.01 0.95 -2.85 2.49 5.33 -0.01 -0.08 0.1
Как видим, теперь средние равны 0, а стандартные отклонения 1 — мы привели переменные к единой шкале.
Теперь, после такого преобразования, мы можем рассчитать итоговый суммарный балл по двум предметам. Используя знакомую процедуру вычисления переменной, вычислим новую переменную, сложив переменные ZMath и ZRus, назовём ее SumZ.
Вопрос 3.3(8)r. Чему будет равно среднее новой переменной?
Упражнение 3.3(9)r. Произведите ранжирование по переменным Sum и SumZ с помощью функции rank и поместите результат в переменные RSum и RSumZ соответственно. Посмотрите таблицу данные с помощью функции Viewи убедитесь, что ранги не совпадают.
Упорядочите наблюдения по переменной SumZ. Убедитесь, что среди лучших двадцати процентов присутствуют абитуриенты лишь с верхними оценками по русскому языку и математике.