У 40 менеджеров по продажам крупной компании измерялись возраст (переменная Age), интеллект (IQ), опыт работы по специальности (WorkExperience), трудовая мотивация (Motivation), коммуникативные навыки (CommunicationSkills), а затем их начальники оценивали их продуктивность по 100-балльной системе (WorkProductivity). Данные приведены в файле WorkProductivity.sav. Задачи перед практическим психологом на основе этих данных могут стоять разные: выяснить связь продуктивности и психологических факторов, обнаружить индикаторы, по которым можно ее предсказать, разработать систему, ориентируясь на которую можно уже при приеме на работу оценить продуктивность будущих сотрудников, и т.п. В любом случае одна из первых задач — установление связи между переменными.
Корреляции между шестью нашими переменными удобно выводить в виде матрицы. Для этого в открывшемся окне после выбора Анализ — Корреляции — Парные (Analyze — Correlation — Bivariate) переносим в поле Переменные (Variables) все наши переменные. После нажатия ОК получаем матрицу.
Таблица 10.3(2). Матрица корреляций
| IQ | WorkExperience | Motivation | CommunicationSkills | Age | WorkProductivity | ||
| IQ | Корреляция Пирсона | 1 | 0.060 | -0.110 | 0.031 | -0.095 | 0.246 |
| Знач. (двухсторонняя) | 0.696 | 0.472 | 0.838 | 0.535 | 0.125 | ||
| N | 45 | 45 | 45 | 45 | 45 | 40 | |
| WorkExperience | Корреляция Пирсона | 0.060 | 1 | -0.038 | -0.048 | 0.151 | 0.376* |
| Знач. (двухсторонняя) | 0.696 | 0.805 | 0.755 | 0.323 | 0.017 | ||
| N | 45 | 45 | 45 | 45 | 45 | 40 | |
| Motivation | Корреляция Пирсона | -0.110 | -0.038 | 1 | -0.126 | -0.093 | 0.342* |
| Знач. (двухсторонняя) | 0.472 | 0.805 | 0.408 | 0.545 | 0.031 | ||
| N | 45 | 45 | 45 | 45 | 45 | 40 | |
| CommunicationSkills | Корреляция Пирсона | 0.031 | -0.048 | -0.126 | 1 | -0.064 | 0.354* |
| Знач. (двухсторонняя) | 0.838 | 0.755 | 0.408 | 0.677 | 0.025 | ||
| N | 45 | 45 | 45 | 45 | 45 | 40 | |
| Age | Корреляция Пирсона | -0.095 | 0.151 | -0.093 | -0.064 | 1 | -0.024 |
| Знач. (двухсторонняя) | 0.535 | 0.323 | 0.545 | 0.677 | 0.885 | ||
| N | 45 | 45 | 45 | 45 | 45 | 40 | |
| WorkProductivity | Корреляция Пирсона | 0.246 | 0.376* | 0.342* | 0.354* | -0.024 | 1 |
| Знач. (двухсторонняя) | 0.125 | 0.017 | 0.031 | 0.025 | 0.885 | ||
| N | 40 | 40 | 40 | 40 | 40 | 40 | |
| *. Корреляция значима на уровне 0,05 (двухсторонняя) | |||||||
На главной диагонали матрицы проставлены единицы (корреляции переменных с собой), в симметричных относительно главной диагонали клетках стоят равные числа, поскольку при расчете корреляций порядок переменных не важен. Под корреляциями подписаны их значимости, а еще ниже количество учтенных парных данных. Заметим, что корреляции интеллекта, опыта работы, мотивации, коммуникативных навыков и возраста крайне слабы: максимальная корреляция составляет 0.15: более старшие работники имеют немного более длительный опыт работы по специальности, что закономерно. Ни в одном случае коэффициенты корреляции не достигают уровня значимости 0.05. Напротив, средние по силе положительные корреляции связывают продуктивность на рабочем месте с опытом работы, мотивацией и коммуникативными навыками.
Таблица, приведенная выше, называется матрицей корреляций. По ней можно сразу оценить значимость каждой корреляции. Однако оценка эта проводится для каждой пары отдельно, а рассчитывается сразу много корреляций (для n переменных матрица содержит \( n(n-1)/2 \) различных корреляций). В этом случае необходима поправка значимости, похожая на ту, с которой мы знакомились в подпараграфе 7.1.4, посвященном апостериорным сравнениям в дисперсионном анализе. Однако до сих пор согласия в статистическом сообществе о такого рода поправках для корреляций нет[1].
У 40 менеджеров по продажам крупной компании измерялись возраст (переменная Age), интеллект (IQ), опыт работы по специальности (WorkExperience), трудовая мотивация (Motivation), коммуникативные навыки (CommunicationSkills), а затем их начальники оценивали их продуктивность по 100-балльной системе (WorkProductivity). Данные приведены в файле WorkProductivity.sav. Задачи перед практическим психологом на основе этих данных могут стоять разные: выяснить связь продуктивности и психологических факторов, обнаружить индикаторы, по которым можно ее предсказать, разработать систему, ориентируясь на которую можно уже при приеме на работу оценить продуктивность будущих сотрудников, и т.п. В любом случае одна из первых задач — установление связи между переменными.
Корреляции между шестью нашими переменными удобно выводить в виде матрицы. Для этого в разделе Analyses выберем Regression – Correlation matrix. Полученная матрица включает коэффициенты корреляций и значимость для них. Матрица треугольная, потому что на ее диагонали стоят единицы (корреляции переменных с самими собой), а верхняя часть не добавляет нам информации – просто зеркально отображает нижнюю часть.
Таблица 10.3(2). Матрица корреляций
| Correlation Matrix | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IQ | Motivation | CommunicationSkills | Age | WorkExperience | WorkProductivity | ||||||||||
| IQ | Pearson’s r | — | |||||||||||||
| p-value | — | ||||||||||||||
| Motivation | Pearson’s r | -0.110 | — | ||||||||||||
| p-value | 0.472 | — | |||||||||||||
| CommunicationSkills | Pearson’s r | 0.031 | -0.126 | — | |||||||||||
| p-value | 0.838 | 0.408 | — | ||||||||||||
| Age | Pearson’s r | -0.095 | -0.093 | -0.064 | — | ||||||||||
| p-value | 0.535 | 0.545 | 0.677 | — | |||||||||||
| WorkExperience | Pearson’s r | 0.060 | -0.038 | -0.048 | 0.151 | — | |||||||||
| p-value | 0.696 | 0.805 | 0.755 | 0.323 | — | ||||||||||
| WorkProductivity | Pearson’s r | 0.246 | 0.342 | 0.354 | -0.024 | 0.376 | — | ||||||||
| p-value | 0.125 | 0.031 | 0.025 | 0.885 | 0.017 | — | |||||||||
Заметим, что корреляции интеллекта, опыта работы, мотивации, коммуникативных навыков и возраста крайне слабы: максимальная корреляция составляет 0.15: более старшие работники имеют немного более длительный опыт работы по специальности, что закономерно. Ни в одном случае коэффициенты корреляции не достигают уровня значимости 0.05. Напротив, средние по силе положительные корреляции связывают продуктивность на рабочем месте с опытом работы, мотивацией и коммуникативными навыками.
Таблица, приведенная выше, называется матрицей корреляций. По ней можно сразу оценить значимость каждой корреляции. Однако оценка эта проводится для каждой пары отдельно, а рассчитывается сразу много корреляций (для n переменных матрица содержит n(n−1)/2 различных корреляций. В этом случае необходима поправка значимости, похожая на ту, с которой мы знакомились в подпараграфе 7.1.4, посвященном апостериорным сравнениям в дисперсионном анализе. Однако до сих пор согласия в статистическом сообществе о такого рода поправках для корреляций нет[1].
У 40 менеджеров по продажам крупной компании измерялись возраст (переменная Age), интеллект (IQ), опыт работы по специальности (WorkExperience), трудовая мотивация (Motivation), коммуникативные навыки (CommunicationSkills), а затем их начальники оценивали их продуктивность по 100-балльной системе (WorkProductivity). Данные приведены в файле WorkProductivity.sav. При этом данные также содержат данные нескольких кандидатов на должность, у них измерены возраст и психологические показатели, однако пока неизвестна продуктивность их работы. Задачи перед практическим психологом на основе этих данных могут стоять разные: выяснить связь продуктивности и психологических факторов, обнаружить индикаторы, по которым можно ее предсказать, разработать систему, ориентируясь на которую можно уже при приеме на работу оценить продуктивность будущих сотрудников, и т.п. В любом случае одна из первых задач — установление связи между переменными.
Расчёт между двумя переменными в R можно cor.test (см. пример 9.3.3r в предыдущей главе). Однако для одновременной оценки корреляций многих переменных удобно выводить результаты в виде матрицы. В R это можно делать различными способами. Самый простой – это использовать функцию cor, задав в качестве аргумента таблицу анализируемых переменных. При этом надо учесть, что в одной из переменных есть пропущенные значения (нет продуктивности работы кандидатов). Если в данных есть пропущенные значения, но исследователь не хочет исключать переменные, в которых они встречаются из анализа, то в функции corследует указать значение дополнительного параметра use – либо use = "pairwise.complete.obs"(включать в анализ полные данные для каждой пары переменных), либо use = "complete.obs"(считать корреляции только для испытуемых/респондентов, у которых нет пропусков ни по одной из включенных в анализ переменных, то есть по матрице полных данных). Используем первую возможность и получим следующую матрицу корреляций (для компактности представления округлим результат до трех знаков после запятой с помощью функцииround):
library(foreign)
data_workProd <- read.spss("WorkProductivity.sav", to.data.frame = T, reencode = "utf8")
round(cor(data_workProd, use = "pairwise.complete.obs"), 3)
IQ WorkExperience Motivation CommunicationSkills Age WorkProductivity
IQ 1.000 0.060 -0.110 0.031 -0.095 0.246
WorkExperience 0.060 1.000 -0.038 -0.048 0.151 0.376
Motivation -0.110 -0.038 1.000 -0.126 -0.093 0.342
CommunicationSkills 0.031 -0.048 -0.126 1.000 -0.064 0.354
Age -0.095 0.151 -0.093 -0.064 1.000 -0.024
WorkProductivity 0.246 0.376 0.342 0.354 -0.024 1.000
Заметим, что корреляции интеллекта, опыта работы, мотивации, коммуникативных навыков и возраста крайне слабы: максимальная корреляция составляет 0.15: более старшие работники имеют немного более длительный опыт работы по специальности, что закономерно. Напротив, средние по силе положительные корреляции связывают продуктивность на рабочем месте с опытом работы, мотивацией и коммуникативными навыками. Таблица, приведенная выше, называется матрицей корреляций. При этом, однако, нельзя определить значимость корреляций, функция corне имеет такой опции. Для оценки значимости получаемых корреляций можно использовать функцию corr.testиз пакета psych. При её вызове по умолчанию выводится три таблицы: коэффициентов корреляций, числа точек для каждой пары переменных (число полных пар данных) и таблица значимостей[7]:
corr.test(data_workProd) Call:corr.test(x = data_workProd) Correlation matrix IQ WorkExperience Motivation CommunicationSkills Age WorkProductivity IQ 1.00 0.06 -0.11 0.03 -0.09 0.25 WorkExperience 0.06 1.00 -0.04 -0.05 0.15 0.38 Motivation -0.11 -0.04 1.00 -0.13 -0.09 0.34 CommunicationSkills 0.03 -0.05 -0.13 1.00 -0.06 0.35 Age -0.09 0.15 -0.09 -0.06 1.00 -0.02 WorkProductivity 0.25 0.38 0.34 0.35 -0.02 1.00 Sample Size IQ WorkExperience Motivation CommunicationSkills Age WorkProductivity IQ 45 45 45 45 45 40 WorkExperience 45 45 45 45 45 40 Motivation 45 45 45 45 45 40 CommunicationSkills 45 45 45 45 45 40 Age 45 45 45 45 45 40 WorkProductivity 40 40 40 40 40 40 Probability values (Entries above the diagonal are adjusted for multiple tests.) IQ WorkExperience Motivation CommunicationSkills Age WorkProductivity IQ 0.00 1.00 1.00 1.00 1.00 1.00 WorkExperience 0.70 0.00 1.00 1.00 1.00 0.25 Motivation 0.47 0.81 0.00 1.00 1.00 0.40 CommunicationSkills 0.84 0.75 0.41 0.00 1.00 0.35 Age 0.54 0.32 0.54 0.68 0.00 1.00 WorkProductivity 0.13 0.02 0.03 0.03 0.88 0.00
Обращаем внимание, что матрица значимостей асимметрична – снизу под диагональю выводятся обычные оценки значимости, а наверху – с поправкой на множественные корреляции. Рассмотрим сначала корреляции без поправок – видно, что в этом случае ни одна из корреляций между независимыми переменными не оценивается как значимая (на уровне p < .05), а связь эффективности работы может быть связана с опытом работы (p = 0.02), мотивацией (p = 0.03) и коммуникативными навыками (p = 0.03).Однако надо иметь в виду, что оценка значимости проводится для каждой пары отдельно и рассчитывается сразу много корреляций (для n переменных матрица содержит n(n−1)/2 различных корреляций). В этом случае необходима поправка значимости, похожая на ту, с которой мы знакомились в подпараграфе 7.1.4, посвященном апостериорным сравнениям в дисперсионном анализе. С такой поправкой значимости выведены в верхней части таблицы, над главной диагональю, и можно увидеть, что в этом случае ни одна значимость не приближается к нулю настолько, чтобы её можно было обсуждать как указывающую на значимость корреляций. Отметим также, что до сих пор согласия в статистическом сообществе об оптимальном способе использования тех или иных видов поправок для корреляций нет[1].
Пример 10.3(3). Применение множественной регрессии в предсказании
Как говорилось в параграфе 9.1, именно задачи предсказания значений зависимой переменной по значениям независимой и оценки точности этого предсказания — основная сфера прямого применения регрессионного анализа. При этом результаты особенно информативны, если независимые переменные не коррелируют. Данные примера 10.3.1 — удобная иллюстрация такой ситуации. Перед психологом в организации стояло две задачи: выяснить, на основе каких индикаторов и насколько точно можно предсказать продуктивность менеджеров, и отобрать из пяти новых кандидатов на работу (номера 41 — 45) потенциально лучшего.
С теми же данными (файл WorkProductivity.sav) проведите множественный регрессионный анализ по той же схеме, что и в параграфе 9.3, но включив в список независимых переменных все пять индикаторов.
Регрессионная модель объясняет 48.2% дисперсии продуктивности на рабочем месте[2], а статистическая оценка значимости: \( F=6.336,p<0.001 \). Это не идеальное предсказание, но для практической сферы — неплохой результат.
Близость корреляций между независимыми переменными нулю в таблице 10.3(2) позволяет нам рассматривать таблицу коэффициентов регрессии с минимальным риском искажений из-за мультиколлинеарности. Обратите внимание, что значимость модели не означает, что все индикаторы одинаково «хороши»: например, возраст не связан с продуктивностью, а связь интеллекта с продуктивностью не достигает принятого уровня значимости 0.05.
Таблица 10.3(5). Регрессионные коэффициенты
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | т | Значимость | ||
| B | Стандартная ошибка | Бета | ||||
| 1 | (Константа) | -75.813 | 36.791 | -2.061 | 0.047 | |
| IQ | 0.518 | 0.288 | 0.225 | 1.797 | 0.081 | |
| WorkExperience | 3.856 | 1.265 | 0.385 | 3.049 | 0.004 | |
| Motivation | 0.884 | 0.263 | 0.418 | 3.356 | 0.002 | |
| CommunicationSkills | 0.902 | 0.289 | 0.391 | 3.126 | 0.004 | |
| Age | -0.057 | 0.497 | -0.014 | -0.114 | 0.910 | |
| a. Зависимая переменная: WorkProductivity | ||||||
Упражнение 10.3(4)j. С теми же данными (файл WorkProductivity.sav) проведите множественный регрессионный анализ по той же схеме, что и в параграфе 9.3, но включив в список независимых переменных все пять индикаторов. Напомним, что в закладке Model Fit важно задать F test (чтобы оценить значимость модели в целом). Поскольку множество независимых переменных требует поправки на их количество – в том же разделе можно поставить галочку на \( R^2 \) adjusted – \( R^2 \)с поправкой на количество независимых переменных в модели (по сути, это «штраф» за количество независимых переменных).
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.694 | 0.482 | 6.336 | 5 | 34 | < .001 | |||||||
Регрессионная модель объясняет 48.2% дисперсии продуктивности на рабочем месте[2], а статистическая оценка значимости: F(5, 34)=6.336,p<0.001. Это не идеальное предсказание, но для практической сферы — неплохой результат.
Близость корреляций между независимыми переменными нулю в таблице 10.3(2) позволяет нам рассматривать таблицу коэффициентов регрессии с минимальным риском искажений из-за мультиколлинеарности. Обратите внимание, что значимость модели не означает, что все индикаторы одинаково «хороши»: например, возраст не связан с продуктивностью, а связь интеллекта с продуктивностью не достигает принятого уровня значимости 0.05.
Таблица 10.3(5)j. Регрессионные коэффициенты
| Model Coefficients — WorkProductivity | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | |||||
| Intercept | -75.813 | 36.791 | -2.061 | 0.047 | |||||
| Age | -0.057 | 0.497 | -0.114 | 0.910 | |||||
| CommunicationSkills | 0.902 | 0.289 | 3.126 | 0.004 | |||||
| Motivation | 0.884 | 0.263 | 3.356 | 0.002 | |||||
| WorkExperience | 3.856 | 1.265 | 3.049 | 0.004 | |||||
| IQ | 0.518 | 0.288 | 1.797 | 0.081 | |||||
Упражнение 10.3(4)r. С теми же данными (файл WorkProductivity.sav) проведите множественный регрессионный анализ по той же схеме, что и в параграфе 9.3, но включив в список независимых переменных все пять индикаторов. Для введения в модель нескольких предикторов в формуле ЗП ~ НП справа можно указать несколько переменных, объединяя их знаком +. Соответственно, для наших данных вызов функции lm будет выглядеть так (сохраним результаты в переменную model_workProd):
model_workProd <- lm(WorkProductivity ~ IQ + WorkExperience + Motivation + CommunicationSkills + Age, data = data_workProd)
Выведем результат с помощью функции summary:
summary(model_workProd) Call: lm(formula = WorkProductivity ~ IQ + WorkExperience + Motivation + CommunicationSkills + Age, data = data_workProd) Residuals: Min 1Q Median 3Q Max -26.337 -9.902 -2.248 12.396 33.840 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -75.81327 36.79073 -2.061 0.04705 * IQ 0.51813 0.28830 1.797 0.08119 . WorkExperience 3.85603 1.26470 3.049 0.00443 ** Motivation 0.88422 0.26347 3.356 0.00196 ** CommunicationSkills 0.90246 0.28871 3.126 0.00362 ** Age -0.05678 0.49726 -0.114 0.90976 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 15.48 on 34 degrees of freedom (5 пропущенных наблюдений удалены) Multiple R-squared: 0.4823, Adjusted R-squared: 0.4062 F-statistic: 6.336 on 5 and 34 DF, p-value: 0.0002953
Можно начать рассмотрение с оценок качества модели в конце отчёта. Как видно, по коэффициенту R-квадрат, регрессионная модель объясняет 48.2% дисперсии продуктивности на рабочем месте[2], а статистическая оценка значимости по результатам дисперсионного анализ составляет F(5, 34)=6.336,p<0.001. Это не идеальное предсказание, но для практической сферы — неплохой результат.
Близость корреляций между независимыми переменными нулю в таблице 10.3(2) позволяет нам рассматривать таблицу коэффициентов регрессии с минимальным риском искажений из-за мультиколлинеарности. Рассмотрите матрицу коэффициентов модели и обратите внимание, что значимость модели не означает, что все индикаторы одинаково «хороши»: например, возраст не связан с продуктивностью, а связь интеллекта с продуктивностью не достигает принятого уровня значимости 0.05.
Упражнение 10.3(6). Проведите регрессионный анализ повторно, убрав из списка независимых переменных сначала возраст, затем — возраст и IQ. Убедитесь, что знание возраста не помогает в предсказании — его удаление не сказывается на R2. Обоснуйте, почему изменяется F-отношение и скорректированный R2.
Удаление из модели переменной IQ приводит к ухудшению ее точности: R2 = 43.2%, даже если судить по скорректированному коэффициенту детерминации «выигрыш» в одну независимую переменную не «перекрывает» проигрыша в объясняемой дисперсии (скорректированный R2 = 38.5%). Важны ли эти 5% объясняемой дисперсии, по сравнению с затратами на проведение теста на интеллект, — решать практику.
Запишем уравнение регрессии в нестандартизованном виде для модели без учета возраста (обратите внимание, что коэффициенты при удалении из модели возраста изменились совсем незначительно): предсказанную моделью продуктивность каждого менеджера можно рассчитать по формуле
\[ y=0.521x_1+3.832x_2+0.885x_3+0.907x_4−77.791 \]
где \( x_{1-4} \) — баллы каждого из менеджеров по интеллекту, опыту работы, мотивации и коммуникации, соответственно.
Упражнение 10.3(7). Сохраните предсказанные нестандартизованные значения и остатки (ошибки) для каждого менеджера. В SPSS это можно сделать, добавив галочку в пункте Остатки — Нестандартизованные (Residuals — Unstandartized), в Jamovi — в разделе Save – Predicted values и Save – Residuals), а в R использовать функцииpredict, использовав качестве первого аргумента переменную с результатами рассчитанной модели, а аргумент newdata приравняв к названию таблицы исходных данных (для расчёта прогнозируемых значений в случае отсутствия зависимой переменной): predict(model_workProd, newdata = data_workProd)и функцию residualsдля расчёта остатков. В SPSS и Jamovi в таблице данных появились не только предсказанная продуктивность, но и индивидуальные отличия этого предсказания от реальной продуктивности каждого менеджера. В R эти данные будут выведены в консоль или сохранены в переменную, если вы дадите соответствующую команду. Убедитесь, что остатки получаются вычитанием из действительной продуктивности предсказанных значений. Метод наименьших квадратов стремится свести сумму квадратов этих остатков по испытуемым (наблюдениям) к минимуму.
Заметим, что величина остатка, являющаяся для математика «ошибкой», может быть важна для психолога: например, у менеджера под номером 22 предсказанная продуктивность 44.37, а в действительности он работает много лучше — на 78. Вопрос о том, что именно, не учтенное в нашей модели, помогает ему в работе (проясненный, например, в интервью с этим человеком или наблюдении за ним), может помочь развитию и теории, и практики психологии.
Наконец, предсказанные значения новых пяти кандидатов можно взять за основу для сравнения: согласно регрессионному уравнению, лучшим будет кандидат № 44 с предсказанной продуктивностью в 57.299 балла.
В завершение примера еще раз обратим внимание, что такое прямое применение множественной регрессии характерно для узких практических задач (предсказания), а интерпретация коэффициентов регрессионного уравнения не вызывает вопросов, только если корреляции независимых переменных близки к нулю, что в психологической реальности — крайне редкий случай. Далее рассмотрим, что происходит в более сложных, но значительно более распространенных ситуациях.
В примере о конфликтности в браке (пример 9.3(8)) мы не обсудили, как можно интерпретировать результат. Является ли долгое разглядывание картинок в экспериментальной ситуации причиной конфликтности отношений в семье через два года? Очевидно, нет, поскольку считанные минуты взаимодействия с картинками в экспериментальной ситуации не могут произвести значительное долговременное воздействие. Скорее, время разглядывания картинок является индикатором, характеризующим состояние какой-то более существенной характеристики супругов. Претендентом на эту роль может оказаться удовлетворенность браком. В файле ConflictM.sav приведены данные эксперимента о связи времени разглядывания картинок с устойчивостью брака, но с добавлением результата анкетирования, по которому оценивалась удовлетворенность браком.
Мы имеем теперь три переменные: lookingtime, conflictness, satisfaction, измеряющие указанные параметры. Матрица корреляций между ними фактически содержит три корреляции: satisfaction дает корреляцию 0.708 с conflictness и 0.598 с lookingtime. Корреляция между conflictness и lookingtime равна 0.537. Иными словами, можно опасаться искажения регрессионных коэффициентов вследствие мультиколлинеарности.
Проведем регрессионный анализ вновь, добавив в окне регрессии к независимым переменным переменную satisfaction, и нажмем ОК.
Рассмотрим три таблицы. В первой мы находим существенное увеличение показателя R2 (с 0.288 в случае простой регрессии с переменной lookingtime — см. 9.3(8), до 0.521), свидетельствующее о возросшем качестве модели (ее регрессионное уравнение мы давали в подпараграфе 9.1.5).
| Сводка для модели | ||||
| Модель | R | R-квадрат | Скорректированный R-квадрат | Стд. ошибка оценки |
| 1 | 0.722a | 0.521 | 0.489 | 1.47457 |
| a. Предикторы: (конст) satisfaction, lookingtime | ||||
Во второй дана общая оценка значимости модели в целом (см. 10.1.2: F-отношение (16.329) и собственно значимость (0.000, что в силу правил округления говорит о том, что значимость по крайней мере меньше 0.0005).
| Дисперсионный анализa | ||||||
| Модель | Сумма квадратов | ст.св. | Средн. квадрат | F | Знч. | |
| Регрессия | 71.012 | 2 | 35.506 | 16.32 | .000b | |
| Остаток | 65.231 | 30 | 2.174 | |||
| Всего | 136.242 | 32 | ||||
| a. Зависимая переменная: conflictness | ||||||
| b. Предикторы: (конст) satisfaction, lookingtime | ||||||
В третьей таблице сначала даны нестандартизованные коэффициенты (свободный член 6.289 и угловые коэффициенты 0.095 для времени разглядывания изображений и 0.328 для удовлетворенности браком). По этим коэффициентам мы можем составить регрессионное уравнение и с точностью более 50% (R-квадрат равен 0.521) предсказывать конфликтность отношений, которую семья будет иметь через два года. О силе связи независимых и зависимой переменных обычно судят по стандартизованным коэффициентам, однако чем выше корреляция между независимыми переменными (а в нашем случае она достаточно высока), тем меньше смысла в такой интерпретации результатов (см. 10.1.2). Ниже мы рассмотрим вопрос подробнее.
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | ||
| B | Стд. ошибка | Бета | ||||
| 1 | (Константа) | 6.289 | 1.982 | 3.172 | 0.003 | |
| lookingtime | 0.095 | 0.085 | 0.176 | 1.119 | 0.272 | |
| satisfaction | 0.328 | 0.086 | 0.602 | 3.820 | 0.001 | |
| a. Зависимая переменная: conflictness | ||||||
Заметим, что наша регрессионная модель оставляет вопрос о статусе времени разглядывания изображений не проясненным. Как мы говорили, статистика сама по себе не может помочь определить направление и характер связей между переменными[3]. Приблизиться к их пониманию позволяет вовсе не статистическая обработка данных, а дизайн исследования. Например, если при проведении эксперимента исследователь сам управляет независимой переменной и пытается контролировать другие переменные — это дает ему некоторые гарантии, что именно то, на что он повлиял (независимая переменная) — причина тех изменений, которые произошли (зависимая переменная, см. Корнилова, 2005).
В примере о конфликтности в браке (пример 9.3(8)j) мы не обсудили, как можно интерпретировать результат. Является ли долгое разглядывание картинок в экспериментальной ситуации причиной конфликтности отношений в семье через два года? Очевидно, нет, поскольку считанные минуты взаимодействия с картинками в экспериментальной ситуации не могут произвести значительное долговременное воздействие. Скорее, время разглядывания картинок является индикатором, характеризующим состояние какой-то более существенной характеристики супругов. Претендентом на эту роль может оказаться удовлетворенность браком. В файле ConflictM.sav приведены данные эксперимента о связи времени разглядывания картинок с устойчивостью брака, но с добавлением результата анкетирования, по которому оценивалась удовлетворенность браком.
Мы имеем теперь три переменные: lookingtime, conflictness, satisfaction, измеряющие указанные параметры. Матрица корреляций между ними фактически содержит три корреляции: satisfaction дает корреляцию 0.708 с conflictness и 0.598 с lookingtime. Корреляция между conflictness и lookingtime равна 0.537. Иными словами, можно опасаться искажения регрессионных коэффициентов вследствие мультиколлинеарности.
Проведем регрессионный анализ вновь, добавив в окне регрессии к независимым переменным переменную satisfaction.
Рассмотрим две таблицы.
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.722 | 0.521 | 16.329 | 2 | 30 | < .001 | |||||||
<
| Model Coefficients — conflictness | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | |||||
| Intercept | 6.289 | 1.982 | 3.172 | 0.003 | |||||
| lookingtime | 0.095 | 0.085 | 1.119 | 0.272 | |||||
| satisfaction | 0.328 | 0.086 | 3.820 | < .001 | |||||
В первой мы находим существенное увеличение показателя R2 (с 0.288 в случае простой регрессии с переменной lookingtime — см. 9.3(8), до 0.521), свидетельствующее о возросшем качестве модели (ее регрессионное уравнение мы давали в подпараграфе 9.1.5). Здесь же дана общая оценка значимости модели в целом (см. 10.1.2: F-отношение (16.3) и собственно значимость (<0.001).
Во второй таблице сначала даны нестандартизованные коэффициенты (свободный член 6.2888 и угловые коэффициенты 0.0947 для времени разглядывания изображений и 0.3278 для удовлетворенности браком). По этим коэффициентам мы можем составить регрессионное уравнение и с точностью более 50% (R-квадрат равен 0.521) предсказывать конфликтность отношений, которую семья будет иметь через два года. О силе связи независимых и зависимой переменных обычно судят по стандартизованным коэффициентам, однако чем выше корреляция между независимыми переменными (а в нашем случае она достаточно высока), тем меньше смысла в такой интерпретации результатов (см. 10.1.2). Ниже мы рассмотрим вопрос подробнее.
Заметим, что наша регрессионная модель оставляет вопрос о статусе времени разглядывания изображений не проясненным. Как мы говорили, статистика сама по себе не может помочь определить направление и характер связей между переменными[3]. Приблизиться к их пониманию позволяет вовсе не статистическая обработка данных, а дизайн исследования. Например, если при проведении эксперимента исследователь сам управляет независимой переменной и пытается контролировать другие переменные — это дает ему некоторые гарантии, что именно то, на что он повлиял (независимая переменная) — причина тех изменений, которые произошли (зависимая переменная, см. Корнилова, 2005).
В примере о конфликтности в браке (пример 9.3(8)) мы не обсудили, как можно интерпретировать результат. Является ли долгое разглядывание картинок в экспериментальной ситуации причиной конфликтности отношений в семье через два года? Очевидно, нет, поскольку считанные минуты взаимодействия с картинками в экспериментальной ситуации не могут произвести значительное долговременное воздействие. Скорее, время разглядывания картинок является индикатором, характеризующим состояние какой-то более существенной характеристики супругов. Претендентом на эту роль может оказаться удовлетворенность браком. В файле ConflictM.sav приведены данные эксперимента о связи времени разглядывания картинок с устойчивостью брака, но с добавлением результата анкетирования, по которому оценивалась удовлетворенность браком.
Мы имеем теперь три переменные: lookingtime, conflictness, satisfaction, измеряющие указанные параметры. Загрузив файл в R можно убедиться, что корреляции между ними будет таковы: satisfaction дает корреляцию 0.708 с conflictness и 0.598 с lookingtime. Корреляция между conflictness и lookingtime равна 0.537. Иными словами, можно опасаться искажения регрессионных коэффициентов вследствие мультиколлинеарности.
Проведем регрессионный анализ вновь, добавив к независимым переменным переменную satisfaction:
model_conflictM <- lm(conflictness ~ lookingtime + satisfaction, data = data_conflictM)
Рассмотрим основные результаты:
summary(model_conflictM) Call: lm(formula = conflictness ~ lookingtime + satisfaction, data = data_conflictM) Residuals: Min 1Q Median 3Q Max -2.5241 -1.0790 0.1203 0.8497 2.7999 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.28883 1.98250 3.172 0.003479 ** lookingtime 0.09465 0.08459 1.119 0.272057 satisfaction 0.32777 0.08580 3.820 0.000625 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.475 on 30 degrees of freedom Multiple R-squared: 0.5212, Adjusted R-squared: 0.4893 F-statistic: 16.33 on 2 and 30 DF, p-value: 1.593e-05
Мы можем отметить существенное увеличение показателя R2 (с 0.288 в случае простой регрессии с переменной lookingtime — см. 9.3(8)r, до 0.521), свидетельствующее о возросшем качестве модели (ее регрессионное уравнение мы давали в подпараграфе 9.1.5).
Также следует обратить внимание на общую оценку значимости модели в целом (см. 10.1.2: F-отношение (F(2, 30)=16.329) и собственно значимость (которая очень близка к нулю, точно равна 0.00001539, в отчёте или работе можно указать что p < 0.001).
Посмотрим также на нестандартизованные коэффициенты модели в начале отчёта: свободный член равен 6.289, а угловые коэффициенты составляют 0.095 для времени разглядывания изображений и 0.328 для удовлетворенности браком. По этим коэффициентам мы можем составить регрессионное уравнение и с точностью более 50% (R-квадрат равен 0.521) предсказывать конфликтность отношений, которую семья будет иметь через два года. О силе связи независимых и зависимой переменных обычно судят по стандартизованным коэффициентам, которые в R можно рассчитать, используя функцию lm.betaиз одноименного пакета:
library(lm.beta) lm.beta(model_conflictM) Call: lm(formula = conflictness ~ lookingtime + satisfaction, data = data_conflictM) Standardized Coefficients:: (Intercept) lookingtime satisfaction 0.0000000 0.1764421 0.6023810
Однако, отметим, что чем выше корреляция между независимыми переменными (а в нашем случае она достаточно высока), тем меньше смысла в такой интерпретации результатов (см. 10.1.2). Ниже мы рассмотрим вопрос подробнее.
Заметим, что наша регрессионная модель оставляет вопрос о статусе времени разглядывания изображений не проясненным. Как мы говорили, статистика сама по себе не может помочь определить направление и характер связей между переменными[3]. Приблизиться к их пониманию позволяет вовсе не статистическая обработка данных, а дизайн исследования. Например, если при проведении эксперимента исследователь сам управляет независимой переменной и пытается контролировать другие переменные — это дает ему некоторые гарантии, что именно то, на что он повлиял (независимая переменная) — причина тех изменений, которые произошли (зависимая переменная, см. Корнилова, 2005).
Пример 10.3(9). Переименуйте переменную lookingtime, присвоив ей имя alcohol. Пусть теперь интерпретация переменных такова: В эксперименте участвовали добровольцы, каждому из которых давали дозу алкоголя (количество в миллилитрах кодируется переменной alcohol). У них затем измеряли уровень ситуативной конфликтности в межличностных отношениях и показатель по тесту «удовлетворенность жизнью». Хотя результат регрессионного анализа будет тем же самым, но смысла он не будет иметь вовсе. При таком экспериментальном дизайне единственной независимой переменной является alcohol, а две другие переменные характеризуют коррелирующие между собой следствия ее изменения.
Важнейший вывод из сказанного: модель множественной регрессии в своих рамках хорошо служит для предсказания результатов и для общей оценки доли дисперсии зависимой переменной, объясняемой совокупностью независимых. Для понимания характера связей нужны содержательный анализ, формулирование разумных гипотез и построение более сложных моделей, учитывающих, что влияние переменной может быть опосредованным другими переменными, что она сама может быть таким посредником (что мы рассмотрим далее).
Пример 10.3(10). «Бессмысленные» интерпретации при мультиколлинеарности нередко имеют место в случаях, если сложные многоуровневые психологические модели проверяются с использованием линейной множественной регрессии. Рассмотрим следующий пример.
Одна из самых известных в психологии здоровья модель предсказания поведения человека — теория запланированного поведения[4]. Она схематически изображена на рис. 10.3(11). Предполагается, что поведение (например, «заниматься спортом два раза в неделю по полчаса») зависит от намерения («Я собираюсь заниматься спортом два раза в неделю по полчаса») и воспринимаемого контроля («Я смогу заниматься спортом два раза в неделю по полчаса»). Намерение, в свою очередь, зависит от установок («Мне полезно заниматься спортом два раза в неделю по полчаса»), субъективных норм («Окружающие считают, что мне нужно заниматься спортом два раза в неделю по полчаса») и того же воспринимаемого контроля
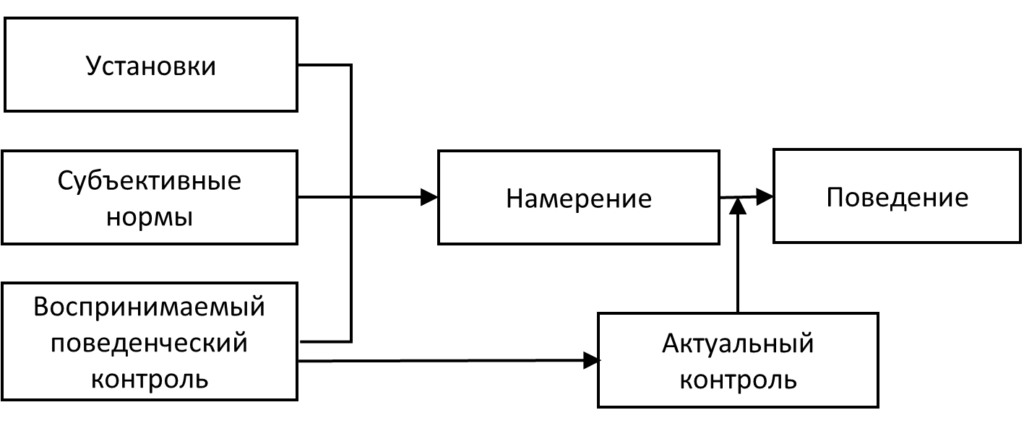 Рис. 10.3(11). Теория запланированного поведения
Рис. 10.3(11). Теория запланированного поведения
В файле HealthBehavior.sav (версия для SPSS, версия для Jamovi ) представлены данные 100 человек, у которых оценивались установки (переменная Attitude), субъективные нормы (переменная SocNorms) и воспринимаемый контроль (переменная Control) в отношении физической зарядки; намерение ее делать (переменная Intention), а через неделю — действительная частота зарядки (переменная Behavior). Каждая переменная оценивалась при помощи оценки приведенных выше утверждений по 10-балльной шкале (0 — полностью не согласен, 10 — полностью согласен).
Упражнение 10.3(12). Рассчитайте матрицу корреляций для всех переменных. По ней предположите (и обоснуйте свое мнение), каковы будут результаты множественной регрессии в отношении поведения (зависимая переменная).
Проведите множественный регрессионный анализ, используя установки, социальные нормы, воспринимаемый контроль и намерение как независимые переменные, а поведение — как зависимую. Проинтерпретируйте результат.
С одной стороны, непосредственные связи «заглушают» действие опосредствованных. Хотя все независимые переменные коррелируют с поведением, в регрессионном анализе исследователь легко обнаружит эффекты намерения и контроля, но не установок и социальных норм, хотя именно последние могут быть крайне важны практически. Например, сказать школьнику «соберись бросить курить» чаще бесполезно, но если на его желание влияют субъективные нормы, можно повлиять на представления его и его друзей о курении и том, как другие реагируют на то, что он курит. С другой стороны, переменные, хорошо предсказывающие результат, могут оказаться хорошими индикаторами, а не факторами, влияющими на зависимую переменную.
Пример 10.3(13). Файл terrible.sav содержит пример, в котором один стандартизованный регрессионный коэффициент больше единицы, а второй — отрицательный несмотря на то, что корреляция зависимой и соответствующей независимой переменных положительная и достаточно большая. Постройте матрицу корреляции и проведите линейную регрессию. Оцените результаты. Пример показывает, что значительная корреляция независимых переменных (мультиколлинеарность) делает регрессионную модель практически бессмысленной. Если учесть, что для некоррелирующих независимых переменных регрессионные коэффициенты равны корреляциям, то под вопросом оказываются те изменения, которые происходят с регрессионными коэффициентами и делают их отличными от корреляций при росте корреляции между независимыми переменными. Также под вопросом оценивание стандартизованными коэффициентами силы связи между переменными.
Задача иерархической регрессии — проверить, отличается ли от нуля уникальный вклад независимых переменных в зависимую после статистического контроля (учета в модели) независимых переменных первого уровня.
В файле WtimeIQ.sav смоделированы данные примера, описанного в подпараграфе 10.2.1 для 30 школьников: у них измерялись «время выдержки» (Wtime), последующая успешность обучения в школе (Success) и дополнительно — интеллект (IQ). Поскольку уровень интеллекта очевидно важный и хорошо изученный фактор успеваемости, основное внимание уделялось вопросу, добавляет ли «время выдержки» дошкольника что-то к предсказанию последующей успеваемости в школе, после учета IQ. Т.е. интеллект — независимая переменная первого уровня, «время выдержки» — второго уровня.
Проведя корреляционный анализ, убедимся, что как интеллект, так и «время выдержки» одинаково тесно связаны с успеваемостью[5] (r=0.52 и r=0.51), но связаны и между собой (r=0.39). Для иерархической регрессии в меню Анализ — Регрессия — Линейная (Analyze — Regression — Linear) найдем над строкой ввода независимых переменных кнопки Предыдущее/Следующее (Next/Previous). Эти кнопки переключают шаги регрессии. Введем IQ в строку независимой переменной и нажмем Next. Теперь во вновь опустевшее окно независимых переменных нужно добавить переменные, дополнительно введенные на шаге 2 (Wtime). Зависимая переменная — Success. Наконец, чтобы оценить изменение процента объясняемой дисперсии на втором шаге иерархической регрессии, нажмем справа кнопку Статистики (Statistics) и выберем Изменение R-квадрат (R squared change).
По результатам дисперсионного анализа обе модели (шаг 1 и после добавления «времени выдержки» на шаге 2) оцениваются приемлемой значимостью (см. таблицу 10.3(15), но, что более важно — добавление новой переменной в модель привело к увеличению R2 с 0.271 до 0.385, т.е. на 11.5%. Это число указана во второй строке столбца Изменение R-квадрат, и при проверке гипотезы об отличии этого изменения от нуля F-отношению, равному 5.044, соответствует значимость 0.033. Можно предположить, что учет «времени выдержки» дополнительно к интеллекту позволяет точнее предсказать успешность младших школьников.
Таблица 10.3(15). Сводки для двух моделей
| Модель | R | R-квадрат | Скорректи-рованный R-квадрат | Стандартная ошибка оценки | Статистика изменений | ||||
| Изме-нение R квадрат | Изменение F | ст.св.1 | ст.св.2 | Знач. Изменение F | |||||
| 1 | 0.520a | 0.271 | 0.244 | 0.86920 | 0.271 | 10.385 | 1 | 28 | 0.003 |
| 2 | 0.621b | 0.385 | 0.340 | 0.81250 | 0.115 | 5.044 | 1 | 27 | 0.033 |
| a. Предикторы: (константа), IQ | |||||||||
| b. Предикторы: (константа), IQ, Wtime | |||||||||
Как видно по таблице коэффициентов (таблица 10.3(16)), эффекты IQ и «времени выдержки» положительные, хотя эффект IQ и снижается при добавлении «времени выдержки» в модель.
Обратим внимание, что исследователя в данном случае не интересует, является ли интеллект первопричиной или первопричина «время выдержки», действует ли одно через другое (медиация), — он лишь описывает наличие или отсутствие уникального вклада независимой переменной, например, чтобы обосновать важность учета «времени выдержки» в дальнейших исследованиях и концепциях.
Таблица 10.3(16). Коэффициенты в двух моделях
| Модель | Нестандартизованные коэффициенты | Стандар-тизованные коэффи-циенты | т | Значимость | ||
| B | Стандартная ошибка | Бета | ||||
| 1 | (Константа) | -2.965 | 1.796 | -1.651 | 0.110 | |
| IQ | 0.056 | 0.018 | 0.520 | 3.223 | 0.003 | |
| 2 | (Константа) | -2.317 | 1.704 | -1.360 | 0.185 | |
| IQ | 0.041 | 0.018 | 0.379 | 2.319 | 0.028 | |
| Wtime | 0.061 | 0.027 | 0.367 | 2.246 | 0.033 | |
| a. Зависимая переменная: Success | ||||||
Задача иерархической регрессии — проверить, отличается ли от нуля уникальный вклад независимых переменных в зависимую после статистического контроля (учета в модели) независимых переменных первого уровня.
В файле WtimeIQ.sav смоделированы данные примера, описанного в подпараграфе 10.2.1 для 30 школьников: у них измерялись «время выдержки» (Wtime), последующая успешность в школе (Success) и дополнительно — интеллект (IQ). Поскольку уровень интеллекта очевидно важный и хорошо изученный фактор успеваемости, основное внимание уделялось вопросу, добавляет ли «время выдержки» дошкольника что-то к предсказанию последующей успеваемости в школе, после учета IQ. Т.е. интеллект — независимая переменная первого уровня, «время выдержки» — второго уровня.
Проведя корреляционный анализ, убедимся, что как интеллект, так и «время выдержки» одинаково тесно связаны с успеваемостью[5] (r=0.52 и r=0.51), но связаны и между собой (r=0.39).
Для иерархической регрессии сначала в обычном меню регрессионного анализа нужно указать, какая переменная – зависимая, какие – ковариаты и факторы. Далее в разделе Model Builder укажите в Block 1 предиктор (независимую переменную) первого уровня – IQ. Добавьте Block 2 c предиктором второго уровня Wtime.
Таблица 10.3(15)j. Сводки для двух моделей
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.520 | 0.271 | 10.385 | 1 | 28 | 0.003 | |||||||
| 2 | 0.621 | 0.385 | 8.464 | 2 | 27 | 0.001 | |||||||
Таблица 10.3(16)j. Коэффициенты в двух моделях
| Model Comparisons | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Comparison | |||||||||||||||
| Model | Model | ΔR² | F | df1 | df2 | p | |||||||||
| 1 | — | 2 | 0.115 | 5.044 | 1 | 27 | 0.033 | ||||||||
По результатам дисперсионного анализа обе модели (шаг 1 и после добавления «времени выдержки» на шаге 2) оцениваются приемлемой значимостью (см. вторую таблицу 10.3(15)j, но, что более важно — добавление новой переменной в модель привело к увеличению R2 с 0.271 до 0.385, т.е. на 11.5%. Это число указана во второй строке столбца Изменение R-квадрат, и при проверке гипотезы об отличии этого изменения от нуля F-отношению, равному 5.04, соответствует значимость 0.033. Можно предположить, что учет «времени выдержки» дополнительно к интеллекту позволяет точнее предсказать успешность младших школьников.
Как видно по таблице коэффициентов, эффекты IQ и «времени выдержки» положительные, хотя эффект IQ и снижается при добавлении «времени выдержки» в модель.
Обратим внимание, что исследователя в данном случае не интересует, является ли интеллект первопричиной или первопричина «время выдержки», действует ли одно через другое (медиация), — он лишь описывает наличие или отсутствие уникального вклада независимой переменной, например, чтобы обосновать важность учета «времени выдержки» в дальнейших исследованиях и концепциях.
Задача иерархической регрессии — проверить, отличается ли от нуля уникальный вклад независимых переменных в зависимую после статистического контроля (учета в модели) независимых переменных первого уровня.
В файле WtimeIQ.sav смоделированы данные примера, описанного в подпараграфе 10.2.1 для 30 школьников: у них измерялись «время выдержки» (Wtime), последующая успешность обучения в школе (Success) и дополнительно — интеллект (IQ). Поскольку уровень интеллекта очевидно важный и хорошо изученный фактор успеваемости, основное внимание уделялось вопросу, добавляет ли «время выдержки» дошкольника что-то к предсказанию последующей успеваемости в школе, после учета IQ. Т.е. интеллект — независимая переменная первого уровня, «время выдержки» — второго уровня.
Проведя корреляционный анализ, убедимся, что как интеллект, так и «время выдержки» одинаково тесно связаны с успеваемостью[5] (r=0.52 и r=0.51), но связаны и между собой (r=0.39).
Для проведения иерархической регрессии в R надо задать нужное количество линейных моделей и сохранить их в разные переменные, чтобы впоследствии их сравнивать между собой. Важно, чтобы модели были вложенными – то есть каждая следующая включала в себя предыдущая с каким-то добавлением. Прямое сравнение невложенных моделей некорретно, надо об этом помнить.
Назовём model1 модель, в которой успешность объясняется только интеллектом, а model2 – модель, включающую в качестве независимой переменной не только показатель интеллекта, но и время выдержки в эксперименте:
model1 <- lm(Success ~ IQ, data = data_wtimeIQ) model2 <- lm(Success ~ IQ + Wtime, data = data_wtimeIQ)
Затем рассмотрим результаты:
summary(model1) Call: lm(formula = Success ~ IQ, data = data_wtimeIQ) Residuals: Min 1Q Median 3Q Max -1.0290 -0.6620 -0.2150 0.3433 2.1479 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2.96524 1.79604 -1.651 0.10992 IQ 0.05647 0.01752 3.223 0.00322 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8692 on 28 degrees of freedom Multiple R-squared: 0.2705, Adjusted R-squared: 0.2445 F-statistic: 10.38 on 1 and 28 DF, p-value: 0.003216 summary(model2) Call: lm(formula = Success ~ IQ + Wtime, data = data_wtimeIQ) Residuals: Min 1Q Median 3Q Max -1.35185 -0.57017 -0.04438 0.32329 1.67270 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2.31731 1.70350 -1.360 0.1850 IQ 0.04114 0.01774 2.319 0.0282 * Wtime 0.06112 0.02722 2.246 0.0331 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8125 on 27 degrees of freedom Multiple R-squared: 0.3854, Adjusted R-squared: 0.3398 F-statistic: 8.464 on 2 and 27 DF, p-value: 0.001401
Как можно увидеть, сопоставив оценку качества двух моделей, добавление новой переменной в модель привело к увеличению R2 с 0.271 до 0.385, т.е. на 11.4%. Насколько существенен это прирост – вопрос содержательный (нам кажется, что объяснение дополнительных 11.5% вариативности успеваемости – это достаточно существенно, но это можно обсуждать). Статистика позволяет оценить значимость отличия этого прироста от 0, используя F-отношение, имеющее в числителе разность средний квадрат разности ошибок в сравниваемых моделях, а в знаменателе – средний квадрат ошибок второй (более сложной или «полной») модели. Для такой оценки в R можно использовать функцию anova, указав в качестве аргументов через запятую сравниваемые вложенные модели (две или больше при необходимости):
anova(model1, model2) Analysis of Variance Table Model 1: Success ~ IQ Model 2: Success ~ IQ + Wtime Res.Df RSS Df Sum of Sq F Pr(>F) 1 28 21.154 2 27 17.824 1 3.3298 5.0439 0.0331 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Как видно из результата, мы получаем F-отношение, равное 5.044\( \frac{(21.154-17.824)/1}{17.824/27}=5.044 \), которому соответствует значимость 0.033. В целом, полученные результаты указывают на то, что учет «времени выдержки» дополнительно к интеллекту позволяет точнее предсказать успешность младших школьников.
Если проанализировать коэффициенты линейных моделей (столбцы estimate в сводных таблицах моделей), можно отметить,что эффекты IQ и «времени выдержки» положительные, хотя эффект IQ и снижается при добавлении «времени выдержки» в модель.
Обратим внимание, что исследователя в данном случае не интересует, является ли интеллект первопричиной или первопричина «время выдержки», действует ли одно через другое (медиация), — он лишь описывает наличие или отсутствие уникального вклада независимой переменной, например, чтобы обосновать важность учета «времени выдержки» в дальнейших исследованиях и концепциях.
Пример 10.3(17). Часто имеет смысл статистически контролировать переменные, вклад которых в зависимую переменную известен и не обсуждается, и переменные других предметных областей (социодемографические факторы, клинические характеристики и т.п.). Еще одна типичная ситуация — необходимость статистически учесть исходный уровень зависимой переменной в исследованиях динамики каких-либо процессов.
Упражнение 10.3(18). В файле SatisfactionСhange.sav приведены показатели изменения в удовлетворенности жизнью людей в начале и середине (через полтора года) экономического кризиса в стране. Помимо этого, оценивались особенности совладания со стрессом по типу конфронтации (Confrontation) — склонность и готовность активно противостоять неприятностям и конфликтам, доказывать свое мнение при разногласиях.
Очевидно, что удовлетворенность жизнью людей — довольно стабильная характеристика; меняется она слабо и зависит от уровня при предыдущем замере. Проведите иерархическую регрессию, используя удовлетворенность при первом замере Satisfaction1 как независимую переменную первого уровня, а Confrontation — как второго. Как легко ожидать, удовлетворенность через полтора года сильно зависит от исходной удовлетворенности (корреляция \( r=0.72,R^2=52.5\% \)). Однако добавление конфронтации приводит к значимому улучшению процента объясняемой дисперсии (пишут: \( \Delta R^2=8\%,p<0.001 \)). Одна из возможных интерпретаций результата: в периоды кризиса именно конфронтация помогает противостоять жизненным трудностям, приводя к улучшению удовлетворенности жизнью.
В примере 9.3(12) мы модифицировали пример со временем просмотра фотографий лиц противоположного пола и конфликтностью, при этом учитывая, родились ли у испытуемых-женщин за два года дети (файл ConflictCB.sav) . На уровне простых регрессий мы видели, что коэффициенты регрессии разные в двух группах (родивших и бездетных). Проверим теперь гипотезу о модерации: рождение детей в браке выступает модератором связи времени просмотра фотографий и конфликтности через два года. Конкретнее, связь есть только у тех, кто к моменту второго замера не успел родить детей. На первом шаге центрируем независимую переменную lookingtime. Для этого рассчитаем ее среднее (15.9162) и, используя команду Преобразование — Вычислить (Transform — Compute), рассчитаем переменную lookingtime_centered = lookingtime − 15.9162.
Упражнение 10.3(20). Убедитесь, что среднее значение новой переменной равно нулю, а стандартное отклонение не изменилось.
Далее при помощи той же команды рассчитаем переменную, характеризующую модерацию, перемножив центрированную переменную lookingtime_centered и переменную ChildBirth, кодированную нулями и единицами[6]: lookingtimebirth = lookingtime_centered * child_birth. Далее проведем иерархический регрессионный анализ для зависимой переменной conflictness, добавив на первом шаге lookingtime_centered и ChildBirth, а на втором — lookingtimebirth.
| Модель | R | R-квадрат | Скорректи-рованный R-квадрат | Стандартная ошибка оценки | Статистика изменений | |||||
| Изме-нение R квадрат | Изменение F | ст.св.1 | ст.св.2 | Знач. Изменение F | ||||||
| 1 | 0.540a | 0.292 | 0.245 | 1.79297 | 0.292 | 6.190 | 2 | 30 | 0.006 | |
| 2 | 0.616b | 0.379 | 0.315 | 1.70802 | 0.087 | 4.059 | 1 | 29 | 0.053 | |
| a. Предикторы: (константа), lookingtime_centered, ChildBirth | ||||||||||
| b. Предикторы: (константа), lookingtime_centered, ChildBirth, lookingtimebirth | ||||||||||
| Коэффициентыa | ||||||
| Модель | Нестандартизованные коэффициенты | Стандартизо-ванные коэффициенты | т | Значимость | ||
| B | Стандартная ошибка | Бета | ||||
| 1 | (Константа) | 17.030 | 0.435 | 39.155 | 0.000 | |
| ChildBirth | .251 | 0.625 | 0.062 | 0.401 | 0.691 | |
| lookingtime_centered | .289 | 0.082 | 0.539 | 3.505 | 0.001 | |
| 2 | (Константа) | 17.016 | 0.414 | 41.062 | 0.000 | |
| ChildBirth | 0.247 | 0.595 | 0.061 | 0.415 | 0.681 | |
| lookingtime_centered | 0.434 | 0.107 | 0.809 | 4.073 | 0.000 | |
| lookingtimebirth | -0.318 | 0.158 | -0.400 | -2.015 | 0.053 | |
| a. Зависимая переменная: conflictness | ||||||
Несмотря на общую значимость модели уже на первом шаге (29.2% объясненной дисперсии конфликтности), рождение ребенка не связано с конфликтностью (\( \beta =0.062 \)) при учете времени просмотра фотографий. Второй шаг добавляет 8.7% объясненной дисперсии, но оценка значимости для улучшения (\( p=0.053 \)) не позволяет сделать уверенный вывод о модерации. Если вопрос нас серьезно интересует, то исследования следует продолжить. Заметим, что регрессионный коэффициент переменной времени просмотра явно изменился, а коэффициент переменной рождения — нет. Итак, хотя в примере 9.3(12) сравнение простых регрессий позволило нам предположить различия между родившими и бездетными женщинами, анализ модерации не подтвердил эту гипотезу.
Если при продолжении исследований мы получили бы уверенное подтверждение гипотезы, то для интерпретации результата надо было бы рассмотреть коэффициенты регрессии, учитывая смысл нуля переменной-модератора:
- В нестандартизованном виде интерпретация была бы такой: модель предсказывает, что увеличение времени просмотра фотографий на единицу у не имеющих детей (ChildBirth = 0) приведет к увеличению конфликтности на 0.434 балла. Такое же увеличение времени просмотра фотографий у родивших детей (ChildBirth = 1) женщин должно (т.е. ожидается в соответствии с моделью) привести к меньшему увеличению конфликтности — на \( 0.434-0.318=0.116 \) балла.
- В стандартизованном виде: модель предсказывает, что увеличение времени просмотра фотографий на одно стандартное отклонение у не имеющих детей (ChildBirth = 0) приведет к увеличению конфликтности в стандартизованном виде на 0.809 этого отклонения. Такое же увеличение времени просмотра фотографий у родивших детей (ChildBirth = 1) женщин должно (т.е. ожидается в соответствии с моделью) привести к меньшему увеличению стандартизованной конфликтности — на \( 0.809-0.400=0.409 \) стандартного отклонения.
В примере 9.3(12) мы модифицировали пример со временем просмотра фотографий лиц противоположного пола и конфликтностью, при этом учитывая, родились ли у испытуемых-женщин за два года дети (файл ConflictCB.sav) . На уровне простых регрессий мы видели, что коэффициенты регрессии разные в двух группах (родивших и бездетных). Проверим теперь гипотезу о модерации: рождение детей в браке выступает модератором связи времени просмотра фотографий и конфликтности через два года. Конкретнее, связь есть только у тех, кто к моменту второго замера не успел родить детей.
Для этого на командной панели справа в разделе Modules нужно скачать расширение medmod. В анализе нужно выбрать Moderation. Модератором (поле Moderator) выступает переменная child_birth, независимая переменная (поле Predictor) – lookingtime, зависимая (поле Dependent Variable) – conflictness. Поставьте галочку на simple slope analysis (анализ простых регрессий) – это нужно, чтобы понять, что означает эффект модерации, если он окажется значимым. В результате будет получено две таблицы:
| Moderation Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Z | p | ||||||
| lookingtime | 0.280 | 0.074 | 3.802 | < .001 | |||||
| child_birth | 0.247 | 0.558 | 0.443 | 0.658 | |||||
| lookingtime ✻ child_birth | -0.318 | 0.148 | -2.149 | 0.032 | |||||
| Simple Slope Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Z | p | ||||||
| Average | 0.280 | 0.079 | 3.561 | < .001 | |||||
| Low (-1SD) | 0.439 | 0.107 | 4.105 | < .001 | |||||
| High (+1SD) | 0.122 | 0.112 | 1.082 | 0.279 | |||||
| Note. shows the effect of the predictor (lookingtime) on the dependent variable (conflictness) at different levels of the moderator (child_birth) | |||||||||
Несмотря на общую значимость модели, рождение ребенка не связано с конфликтностью (β=0.247, p=0.658) при учете времени просмотра фотографий.
Однако связь времени просмотра фото и конфликтности разная у женщин, родивших за это время ребенка и не родивших. Это видно в последней строке первой таблицы , где и описывается эффект модерации: он достигает уровня значимости p<0,032. Другими словами, в целом, чем дольше женщина смотрит на фото лиц противоположного пола, тем больше конфликтов впоследствии в ее семье (это основной эффект, первая строка таблицы), но этот эффект выше у тех, кто не родил ребенка (об этом говорит отрицательный коэффициент в третьей строке: чем выше показатель «рождение ребенка», тем ниже связь). В нашем случае «выше показатель рождение ребенка» означает «ребенок есть» (1 балл) в отличие от «ребенка нет» (0 баллов). А значит у родивших женщин связь слабее, чем у нерожавших.
В таблице Simple slope analysis можно увидеть, как эффект различается (по сравнению со средним по выборке в целом – первая строка Average) у тех, кто на одно стандартное отклонение выше среднего по показателю «рождение детей» (поскольку у нас показатель в номинативной шкале, это означает – у тех, кто родил ребенка), и у тех, кто на одно стандартное отклонение ниже среднего (не рожал). Согласно таблице, у тех, кто не родил, время просмотра фото предсказывает конфликтность, а у тех, кто рожал – нет. Еще раз обратим внимание, что сама конфликтность у них не меньше – просто она не связана с интересом к фото противоположного пола за два года до оценки уровня конфликтов.
Упражнение 10.3(20)j. Убедитесь, что, если Вы поменяете местами независимую переменную и модератор, результат не изменится.
Пример 10.3(19)r. Анализ модерации в Rstudio.
В примере 9.3(12) мы модифицировали пример со временем просмотра фотографий лиц противоположного пола и конфликтностью, при этом учитывая, родились ли у испытуемых-женщин за два года дети (файл ConflictCB.sav) . На уровне простых регрессий мы видели, что коэффициенты регрессии разные в двух группах (родивших и бездетных). Проверим теперь гипотезу о модерации: рождение детей в браке выступает модератором связи времени просмотра фотографий и конфликтности через два года. Конкретнее, связь есть только у тех, кто к моменту второго замера не успел родить детей.
Самый простой вариант, позволяющий провести такой анализ в R – это использовать функцию modиз пакета medmod. В этой функции надо указать данные, с которыми мы работаем (аргумент data), и названия переменных, включенных в анализ, в кавычках: зависимой переменной (аргумент dep), предиктора (аргумент pred) и модератора (аргумент mod). При этом надо следить, чтобы модератор представлял собой числовую шкалу, в нашем случае – это должна быть бинарная шкала, в которой не имеющие детей получат значение 0, а имеющие – 1. Так как исходно переменная child_birth имеет тип фактор, в котором не имеющие детей закодированы числом 1, а имеющие – числом 2 закодирована как фактор преобразуем её в числовую бинарную шкалу:
data_conflictCB$child_birth_binary <- as.numeric(data_conflictCB$child_birth)-1
После этого зададим и рассчитаем модель, указав значение TRUE для двух дополнительных параметров simpleSlopeEst и simpleSlopePlot, чтобы получить дополнительные данные о характере модерации и её визуализацию:
library(medmod) mod(data = data_conflictCB, dep = "conflictness", mod = "child_birth_binary", pred = "lookingtime", simpleSlopeEst = TRUE, simpleSlopePlot = TRUE)
В результате будет получено две таблицы:
MODERATION Moderation Estimates ───────────────────────────────────────────────────────────────────────────────────────── Estimate SE Z p ───────────────────────────────────────────────────────────────────────────────────────── lookingtime 0.2802362 0.07369836 3.8024747 0.0001433 child_birth_binary 0.2468188 0.55770830 0.4425590 0.6580848 lookingtime:child_birth_binary -0.3175544 0.14776462 -2.1490559 0.0316300 ───────────────────────────────────────────────────────────────────────────────────────── SIMPLE SLOPE ANALYSIS Simple Slope Estimates ─────────────────────────────────────────────────────────────────── Estimate SE Z p ─────────────────────────────────────────────────────────────────── Average 0.2802362 0.07870637 3.560527 0.0003701 Low (-1SD) 0.4389405 0.10692144 4.105261 0.0000404 High (+1SD) 0.1215319 0.11237260 1.081508 0.2794712 ─────────────────────────────────────────────────────────────────── Note. shows the effect of the predictor (lookingtime) on the dependent variable (conflictness) at different levels of the moderator (child_birth_binary)
Из первой модели видно, что рождение ребенка не связано с конфликтностью (угловой коэффициент равен 0.247, p=0.658) при учете времени просмотра фотографий. Однако связь времени просмотра фото и конфликтности разная у женщин, родивших за это время ребенка и не родивших. Это видно в последней строке первой таблицы, где и описывается эффект модерации: он достигает уровня значимости p=0.032. Другими словами, в целом, чем дольше женщина смотрит на фото лиц противоположного пола, тем больше конфликтов впоследствии в ее семье (это основной эффект, первая строка таблицы), но этот эффект выше у тех, кто не родил ребенка (об этом говорит отрицательный коэффициент в третьей строке: чем выше показатель «рождение ребенка», тем ниже связь). В нашем случае «выше показатель рождение ребенка» означает «ребенок есть» (1 балл) в отличие от «ребенка нет» (0 баллов). А значит у родивших женщин связь слабее, чем у нерожавших. Прямая интерпретация коффицентов может быть такова: модель предсказывает, что увеличение времени просмотра фотографий на единицу у не имеющих детей (ChildBirth = 0) приведет к увеличению конфликтности на 0.434 балла. Такое же увеличение времени просмотра фотографий у родивших детей (ChildBirth = 1) женщин должно (т.е. ожидается в соответствии с моделью) привести к меньшему увеличению конфликтности — на 0.434−0.318=0.116 балла.
В таблице Simple slope analysis можно увидеть, как эффект различается (по сравнению со средним по выборке в целом – первая строка Average) у тех, кто на одно стандартное отклонение выше среднего по показателю «рождение детей» (поскольку у нас показатель в номинативной шкале, это означает – у тех, кто родил ребенка), и у тех, кто на одно стандартное отклонение ниже среднего (не рожал). Согласно таблице, у тех, кто не родил, время просмотра фото предсказывает конфликтность, а у тех, кто рожал – нет. Еще раз обратим внимание, что сама конфликтность у них не меньше – просто она не связана с интересом к фото противоположного пола за два года до оценки уровня конфликтов.
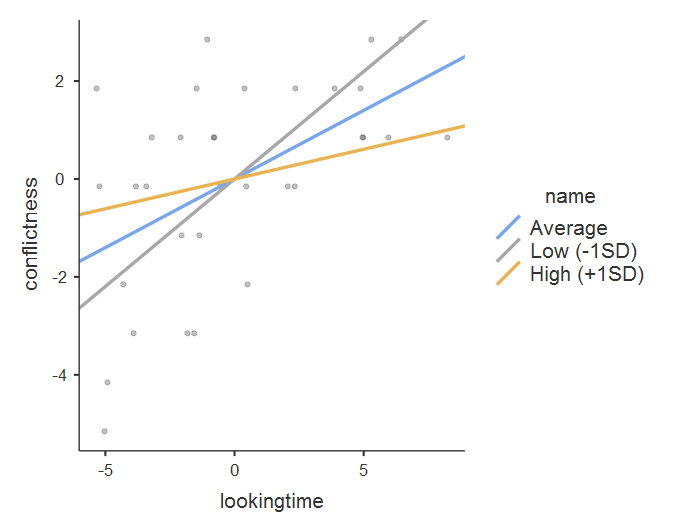
Также полученный результат можно представить графически. На рис. 10.3(20)r представлено три линии регрессии – для всей выборке без учёта модерации (синия линия Average), для тех, у кого нет детей (серая линия, -1SD) и для тех, у кого есть дети (оранжевая линия, +1SD). На графике наглядно видно, что угол регрессионных прямых меняется при учете модератора таким образом, что не имеющие детей женщины демонстрируют более отчётливое увеличение конфликтности по мере увеличения времени просмотра журналов.
Рисунок 10.3(20)r. Регрессионные прямы при учёте модератора
Упражнение 10.3(21)j. Убедитесь, что, если Вы поменяете местами независимую переменную и модератор, результат не изменится.
- В нестандартизованном виде интерпретация была бы такой: модель предсказывает, что увеличение времени просмотра фотографий на единицу у не имеющих детей (ChildBirth = 0) приведет к увеличению конфликтности на 0.434 балла. Такое же увеличение времени просмотра фотографий у родивших детей (ChildBirth = 1) женщин должно (т.е. ожидается в соответствии с моделью) привести к меньшему увеличению конфликтности — на 0.434−0.318=0.116 балла.
- В стандартизованном виде: модель предсказывает, что увеличение времени просмотра фотографий на одно стандартное отклонение у не имеющих детей (ChildBirth= 0) приведет к увеличению конфликтности в стандартизованном виде на 0.809 этого отклонения. Такое же увеличение времени просмотра фотографий у родивших детей (ChildBirth = 1) женщин должно (т.е. ожидается в соответствии с моделью) привести к меньшему увеличению стандартизованной конфликтности — на 809−0.400=0.409 стандартного отклонения.
Вернемся к примеру 9.3.8 о связи времени просмотра фотографий противоположного пола, удовлетворенности и конфликтности в браке и рассмотрим более подходящий способ проверки нашей гипотезы – анализ медиации. Мы предполагали, что время просмотра – индикатор неудовлетворенности, а сама неудовлетворенность сказывается на конфликтности через два года. Файл ConflictM_mediation.sav содержит те же данные, что обсуждались выше, но с сокращенными до 8 символов названиями переменных (таково ограничение макроса, который мы будем использовать ниже).
Пример 10.3.(22). Проведем иерархический регрессионный анализ, на первом шаге которого независимая переменная – looktime, на втором к ней добавляется satisfac, а зависимая переменная – conflict. Результат первого шага полностью повторяет таблицу, полученную в упражнении 9.3(8), а второго шага – в примере 10.3.(8). Только теперь мы видим эти результаты одновременно.
| Коэффициентыa | ||||||
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | т | Значимость | ||
| B | Стандартная ошибка | Бета | ||||
| 1 | (Константа) | 12,567 | 1,330 | 9,450 | ,000 | |
| looktime | ,288 | ,081 | ,537 | 3,544 | ,001 | |
| 2 | (Константа) | 6,289 | 1,982 | 3,172 | ,003 | |
| looktime | ,095 | ,085 | ,176 | 1,119 | ,272 | |
| satisfac | ,328 | ,086 | ,602 | 3,820 | ,001 | |
| a. Зависимая переменная: conflict | ||||||
На первом шаге время просмотра фотографий было значимо связано с конфликтностью через два года; на первом шаге эта связь перестает быть значимой, но добавляется значимая связь удовлетворенности браком и конфликтности. До развития методов модерации, исследователи полагали, что этих результатов (изменения коэффициента при независимой переменной со значимого до незначимого) было достаточно, чтобы сделать вывод о так называемой «полной» медиации – т.е. сказать, что вклад времени просмотра в конфликтность полностью объясняется удовлетворенностью. Если коэффициент снижался, но оставался значимым, говорили о возможной неполной медиации и рассчитывали ее значимость по специальным критериям (например, тесту Собеля).
Современной альтернативой считается оценка прямого и косвенного эффектов при помощи бутстрепа. Для ее проведения в SPSS скачайте макрос process, разработанный Э.Хейесом и находящийся в открытом доступе (по ссылке http://processmacro.org/download.html). Макрос можно активировать по мере надобности или установить постоянно; кроме того, его можно использовать для широкого круга значительно более сложных моделей, нежели те, о которых идет речь в данном учебнике (графическое изображение моделей и их номера в макросе process можно найти в файле templates.pdf, а подробное изложение теории и практики использования этого макроса и методов анализа медиации и модерации можно найти в книге Hayes A. F. Introduction to mediation, moderation, and conditional process analysis: A regression-based approach. – Guilford publications, 2017).
Для активации макроса в командной строке SPSS выберите Файл – Открыть – Синтаксис (File – Open – Syntax) и найдите файл синтаксиса process.sps из папки PROCESS v3.5 for SPSS в скаченном с сайта архиве. Открывшийся файл должен выглядеть так:
Выберите Запуск – Все (Run – All) – и макрос будет работать до выключения SPSS. Теперь для проведения анализа медиации по нашим данным, понадобится синтаксис, описывающий, что и с какой целью требуется рассчитать. Синтаксис для нашего примера в файле ConflictM_mediation.sps.
В нем за командой process перечислены роли каждой переменной (y = conflict – зависимая переменная, x = looktime – независимая, m = satisfac – медиатор). Номер модели (model = 4) указывает на тип (в данном случае – простая медиация; полный перечень в файле templates.pdf). Далее указывается количество подвыборок, которые будут извлечены методом бутстрепа (в нашем случае boot=10000; по умолчанию process использует 5000 извлечений). Если теперь нажать Запуск – Все (Run – All), мы получим следующий вывод:
Run MATRIX procedure: **************** PROCESS Procedure for SPSS Version 3.5.3 **************** Written by Andrew F. Hayes, Ph.D. www.afhayes.com Documentation available in Hayes (2018). www.guilford.com/p/hayes3 ************************************************************************** Model : 4 Y : conflict X : looktime M : satisfac Sample Size: 33 ************************************************************************** OUTCOME VARIABLE: satisfac Model Summary R R-sq MSE F df1 df2 p .5985 .3582 9.5274 17.3010 1.0000 31.0000 .0002 Model coeff se t p LLCI ULCI constant 19.1541 2.3209 8.2529 .0000 14.4205 23.8877 looktime .5901 .1419 4.1594 .0002 .3007 .8794 ************************************************************************** OUTCOME VARIABLE: conflict Model Summary R R-sq MSE F df1 df2 p .7220 .5212 2.1744 16.3294 2.0000 30.0000 .0000 Model coeff se t p LLCI ULCI constant 6.2888 1.9825 3.1722 .0035 2.2399 10.3377 looktime .0947 .0846 1.1189 .2721 -.0781 .2674 satisfac .3278 .0858 3.8200 .0006 .1525 .5030 ************************** TOTAL EFFECT MODEL **************************** OUTCOME VARIABLE: conflict Model Summary R R-sq MSE F df1 df2 p .5370 .2883 3.1277 12.5594 1.0000 31.0000 .0013 Model coeff se t p LLCI ULCI constant 12.5669 1.3298 9.4502 .0000 9.8547 15.2791 looktime .2880 .0813 3.5439 .0013 .1223 .4538 ************** TOTAL, DIRECT, AND INDIRECT EFFECTS OF X ON Y ************** Total effect of X on Y Effect se t p LLCI ULCI c_ps c_cs .2880 .0813 3.5439 .0013 .1223 .4538 .1396 .5370 Direct effect of X on Y Effect se t p LLCI ULCI c'_ps c'_cs .0947 .0846 1.1189 .2721 -.0781 .2674 .0459 .1764 Indirect effect(s) of X on Y: Effect BootSE BootLLCI BootULCI satisfac .1934 .0684 .0781 .3465 Partially standardized indirect effect(s) of X on Y: Effect BootSE BootLLCI BootULCI satisfac .0937 .0292 .0451 .1613 Completely standardized indirect effect(s) of X on Y: Effect BootSE BootLLCI BootULCI satisfac .3605 .1035 .1653 .5719 *********************** ANALYSIS NOTES AND ERRORS ************************ Level of confidence for all confidence intervals in output: 95.0000 Number of bootstrap samples for percentile bootstrap confidence intervals: 10000 –– END MATRIX –--
В первой части приведены результаты простой регрессии с независимой переменной looktime и зависимой satisfac (т.е. медиатор используется как зависимая переменная).
Во второй части – результаты множественной регрессии с независимыми переменными looktime и satisfac и зависимой переменной conflict, которые мы уже видели выше на втором шаге иерархической регрессии.
Третья часть содержит информацию о прямом и косвенном эффектах. Как видим, прямой эффект составляет 0.0947 и он не достигает принятого в психологическом сообществе уровня значимости, а 95%-й доверительный интервал для него составляет (-0.0781-0.2674). Косвенный эффект составляет 0.1934, а метод бутстрепа дает 95%-й доверительный интервал для него равный (0.0869-0.3621). То есть если бы этот косвенный эффект совпадал с теоретическим (в генеральной совокупности), в 95% случаев в исследовании мы получили бы значения, попадающие в этот интервал. Как говорилось в главе 5, напрямую это не доказывает «истинности» косвенного эффекта, но позволяет сориентироваться, основываясь на радиусе интервала и его отношении к нулю. В нашем случае доверительный интервал прямого эффекта накрывает собой ноль, а косвенного нет, что повышает нашу уверенность в косвенном эффекте, хотя и не доказывает его полностью.
Упражнение 10.3(23). Проведите анализ повторно, указав в бутстрепе 1000, 5000 и 100000 подвыборок (в последнем случае приготовьтесь подождать) и сравните полученные радиусы доверительных интервалов косвенного эффекта.
Упражнение 10.3(24). Вернемся к примеру, в котором рассматривались психологические факторы, помогающих людям делать зарядку (упражнение 10.3(12) в файле HealthBehavior.sav.
Используя Файл – Создать – Редактор синтаксиса (File – New – Syntax), создайте новый синтаксис для выявления прямого и косвенного (через медиатор-намерение Intention) эффекта воспринимаемого контроля (Control) на поведение (Behavior). Обратите внимание, что process не допускает длину переменных более 8 знаков (переменные можно переименовать в закладке Представление переменные (Variable View) внизу окна).
По результатам можно заключить о значимом как прямом (95%-й доверительный интервал для 5000 извлечений бутстрепом 0.0960-0.3370), так и косвенном эффектах (0.0134-0.1779) воспринимаемого контроля, что согласуется с рисунком 10.3(11).
Замечание. В process косвенный эффект рассчитывается перемножением двух эффектов (независимая переменная – медиатор и медиатор – зависимая переменная). Этот способ считается достаточно точным, если медиатор и зависимая переменная представлены в численных шкалах. Если же медиатор выражен в бинарной шкале или зависимая переменная – это количество каких-либо объектов, полученных пересчетом (например, число повторных госпитализаций пациентов), то рекомендуется применять другие методы (так называемую причинную медиацию, causal mediation), техническая реализация которых есть в других статистических пакетах (например, R и Mplus).
Вернемся к примеру 9.3.8 о связи времени просмотра фотографий противоположного пола, удовлетворенности и конфликтности в браке и рассмотрим более подходящий способ проверки нашей гипотезы – анализ медиации. Мы предполагали, что время просмотра – индикатор неудовлетворенности, а сама неудовлетворенность сказывается на конфликтности через два года. Данные содержатся в файле ConflictM.sav содержит те же данные, что обсуждались выше, но с сокращенными до 8 символов названиями переменных (таково ограничение макроса, который мы будем использовать ниже).
Пример 10.3.(22)j. Проведем иерархический регрессионный анализ, на первом шаге которого независимая переменная – lookingtime, на втором к ней добавляется satisfaction, а зависимая переменная – conflict. Результат первого шага (model 1) полностью повторяет таблицу, полученную в упражнении 9.3.8 , а второго шага (model 2) – в примере 10.3.(8)j. Только теперь мы видим эти результаты одновременно.
Model 1
| Model Coefficients — conflict | |||||||||
| Predictor | Estimate | SE | t | p | |||||
| Intercept | 12.567 | 1.330 | 9.450 | < .001 | |||||
| lookingtime | 0.288 | 0.081 | 3.544 | 0.001 | |||||
Model 2
| Model Coefficients — conflict | |||||||||
| Predictor | Estimate | SE | t | p | |||||
| Intercept | 6.289 | 1.982 | 3.172 | 0.003 | |||||
| lookingtime | 0.095 | 0.085 | 1.119 | 0.272 | |||||
| satisfaction | 0.328 | 0.086 | 3.820 | < .001 | |||||
На первом шаге время просмотра фотографий было значимо связано с конфликтностью через два года; на первом шаге эта связь перестает быть значимой, но добавляется значимая связь удовлетворенности браком и конфликтности. До развития методов модерации, исследователи полагали, что этих результатов (изменения коэффициента при независимой переменной со значимого до незначимого) было достаточно, чтобы сделать вывод о так называемой «полной» медиации – т.е. сказать, что вклад времени просмотра в конфликтность полностью объясняется удовлетворенностью. Если коэффициент снижался, но оставался значимым, говорили о возможной неполной медиации и рассчитывали ее значимость по специальным критериям (например, тесту Собеля).
Современной альтернативой считается оценка прямого и косвенного эффектов при помощи бутстрепа. В Jamovi это возможно сделать с помощью расширения medmod, которое можно скачать в меню Modules. В появившемся после этого разделе меню medmod нужно выбрать пункт Mediation. Затем в появившемся меню необходимо указать зависимую переменную (поле Dependent variable) – в нашем случае conflict, медиатор (поле Mediator) – satisfaction и независимую переменную (поле Predictor) – lookingtime. В этом расширении Jamovi реализованы два варианта расчет стандартной ошибки для прямого и косвенного эффектов – Standard – аналитический, с допущением о нормальном распределении статистик и Bootstrap – с использованием метода бутстрепа, при котором из имеющейся выборки многократно извлекаются случайные подвыборки, проводится анализ, полученная статистика накапливается и затем по ней рассчитываются эмпирическое значение той или иной статистики. Мы рассмотрим результаты, полученным обоими методами, они представлены в таблицах:
При стандартном способе расчета стандартной ошибок.
| Mediation Estimates | |||||||||||||
| 95% Confidence Interval | |||||||||||||
| Effect | Estimate | SE | Lower | Upper | Z | p | |||||||
| Indirect | 0.193 | 0.066 | 0.064 | 0.323 | 2.929 | 0.003 | |||||||
| Direct | 0.095 | 0.081 | -0.063 | 0.253 | 1.174 | 0.241 | |||||||
| Total | 0.288 | 0.079 | 0.134 | 0.442 | 3.656 | < .001 | |||||||
При расчете стандартных ошибок методом бутстрепа
| Mediation Estimates | |||||||||||||
| 95% Confidence Interval | |||||||||||||
| Effect | Estimate | SE | Lower | Upper | Z | p | |||||||
| Indirect | 0.193 | 0.066 | 0.085 | 0.339 | 2.932 | 0.003 | |||||||
| Direct | 0.095 | 0.071 | -0.026 | 0.260 | 1.334 | 0.182 | |||||||
| Total | 0.288 | 0.081 | 0.141 | 0.455 | 3.536 | < .001 | |||||||
Как видим, прямой эффект составляет 0.095 и он не достигает принятого в психологическом сообществе уровня значимости, а 95%-й доверительный интервал для него при использовании стандартного метода составляет (-0.063; 0.253), а полученный методом бутстрепа при 1000 повторений составил (-0.026; 0.260) – при этом у читателя должен получиться похожий, но несколько другой результат, так как бутстреп каждый раз генерирует новые подвыборки). Косвенный эффект составляет 0.193, он может быть оценен как значимый (p=0.003), стандартно рассчитанный доверительный интервал для этого коэффициента составляет (0.064; 0.323), а метод бутстрепа при нашем расчете дал 95%-й доверительный интервал (0.085-0.339). То есть если бы этот косвенный эффект совпадал с теоретическим (в генеральной совокупности), в 95% случаев в исследовании мы получили бы значения, попадающие в этот интервал. Как говорилось в главе 5, напрямую это не доказывает «истинности» косвенного эффекта, но позволяет сориентироваться, основываясь на радиусе интервала и его отношении к нулю. В нашем случае доверительный интервал прямого эффекта накрывает собой ноль, а косвенного это неверно, что повышает нашу уверенность в косвенном эффекте, хотя и не доказывает его полностью.
Упражнение 10.3(23)j. Проведите анализ повторно, указав в бутстрепе 5000 и 10000 подвыборок (в последнем случае приготовьтесь подождать) и сравните полученные радиусы доверительных интервалов косвенного эффекта.
Упражнение 10.3(24)j. Вернемся к примеру, в котором рассматривались психологические факторы, помогающих людям делать зарядку (упражнение 10.3(12) в файле HealthBehavior.sav.
Используя меню Analyses – Medmod – Mediation проведите анализ, направленный на выявление прямого и косвенного (через медиатор-намерение Intention) эффекта воспринимаемого контроля (Control) на поведение (Behavior). Обратите внимание, что process не допускает длину переменных более 8 знаков (переменные можно переименовать в закладке Представление переменные (Variable View) внизу окна).
По результатам можно заключить о значимом как прямом (95%-й доверительный интервал при стандартном методе расчета (0.099; 0.334), p<0.001), так и косвенном эффектах (доверительный интервал (0.006; 0.171), p=0.035) воспринимаемого контроля, что согласуется с рисунком 10.3(11).
Замечание. В этом расширении косвенный эффект рассчитывается перемножением двух эффектов (независимая переменная – медиатор и медиатор – зависимая переменная). Этот способ считается достаточно точным, если медиатор и зависимая переменная представлены в численных шкалах. Если же медиатор выражен в бинарной шкале или зависимая переменная – это количество каких-либо объектов, полученных пересчетом (например, число повторных госпитализаций пациентов), то рекомендуется применять другие методы (так называемую причинную медиацию, causal mediation), техническая реализация которых есть в других статистических пакетах (например, R и Mplus).
Проведем иерархический регрессионный анализ, на первом шаге которого независимая переменная – lookingtime, на втором к ней добавляется satisfaction, а зависимая переменная – conflictness. Результат первого шага (model1) полностью повторяет таблицу, полученную в упражнении 9.3.8 , а второго шага (model2) – в примере 10.3.(8)j. Только теперь мы видим эти результаты одновременно.
library(foreign)
library(medmod)
data_conflictM <- read.spss("conflictM.sav", to.data.frame = T, reencode = "utf8")
model1 <- lm(conflictness ~ lookingtime, data = data_conflictM)
model2 <- lm(conflictness ~ lookingtime + satisfaction, data = data_conflictM)
summary(model1)
Call:
lm(formula = conflictness ~ lookingtime, data = data_conflictM)
Residuals:
Min 1Q Median 3Q Max
-3.7031 -0.8666 0.0089 1.1711 3.3853
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.56687 1.32979 9.450 1.22e-10 ***
lookingtime 0.28805 0.08128 3.544 0.00127 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.769 on 31 degrees of freedom
Multiple R-squared: 0.2883, Adjusted R-squared: 0.2654
F-statistic: 12.56 on 1 and 31 DF, p-value: 0.001274
summary(model2)
Call:
lm(formula = conflictness ~ lookingtime + satisfaction, data = data_conflictM)
Residuals:
Min 1Q Median 3Q Max
-2.5241 -1.0790 0.1203 0.8497 2.7999
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.28883 1.98250 3.172 0.003479 **
lookingtime 0.09465 0.08459 1.119 0.272057
satisfaction 0.32777 0.08580 3.820 0.000625 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.475 on 30 degrees of freedom
Multiple R-squared: 0.5212, Adjusted R-squared: 0.4893
F-statistic: 16.33 on 2 and 30 DF, p-value: 1.593e-05
На первом шаге время просмотра фотографий было значимо связано с конфликтностью через два года; на первом шаге эта связь перестает быть значимой, но добавляется значимая связь удовлетворенности браком и конфликтности. До развития методов модерации, исследователи полагали, что этих результатов (изменения коэффициента при независимой переменной со значимого до незначимого) было достаточно, чтобы сделать вывод о так называемой «полной» медиации – т.е. сказать, что вклад времени просмотра в конфликтность полностью объясняется удовлетворенностью. Если коэффициент снижался, но оставался значимым, говорили о возможной неполной медиации и рассчитывали ее значимость по специальным критериям (например, тесту Собеля).
Современной альтернативой считается оценка прямого и косвенного эффектов при помощи бутстрепа. В R это возможно сделать, в частности, с помощью функции medбиблиотеки medmod. В качестве аргументов надо указать: название набора данных (параметр data), зависимую переменную (параметр dep) – в нашем случае conflictness, медиатор (параметр med) – satisfaction и независимую переменную (параметр pred) – lookingtime. При этом в функции реализованы два варианта расчет стандартной ошибки для прямого и косвенного эффектов (дополнительный параметр estMethod) – standard – аналитический, с допущением о нормальном распределении статистик и bootstrap – с использованием метода бутстрепа, при котором из имеющейся выборки многократно извлекаются случайные подвыборки, проводится анализ, полученная статистика накапливается и затем по ней рассчитываются эмпирическое значение той или иной статистики. Мы рассмотрим результаты, полученным обоими методами, они представлены в таблицах:
При стандартном способе расчета стандартной ошибок.
med(data = data_conflictM, dep = "conflictness", med = "satisfaction", pred="lookingtime", estMethod = "standard", ci = TRUE) MEDIATION Mediation Estimates ────────────────────────────────────────────────────────────────────────────────────────────────────────── Effect Estimate SE Lower Upper Z p ────────────────────────────────────────────────────────────────────────────────────────────────────────── Indirect 0.19339832 0.06603795 0.06396632 0.3228303 2.928594 0.0034050 Direct 0.09465117 0.08065544 -0.06343059 0.2527329 1.173525 0.2405854 Total 0.28804949 0.07877831 0.13364684 0.4424521 3.656457 0.0002557 ──────────────────────────────────────────────────────────────────────────────────────────────────────────
При расчете стандартных ошибок методом бутстрепа
med(data = data_conflictM, dep = "conflictness", med = "satisfaction", pred="lookingtime", estMethod = "bootstrap", ci = TRUE) MEDIATION Mediation Estimates ──────────────────────────────────────────────────────────────────────────────────────────────────── Effect Estimate SE Lower Upper Z p ──────────────────────────────────────────────────────────────────────────────────────────────────── Indirect 0.19339832 0.07091303 0.07645720 0.3492047 2.727261 0.0063863 Direct 0.09465117 0.07611354 -0.03083411 0.2786176 1.243552 0.2136644 Total 0.28804949 0.08306303 0.12853937 0.4616792 3.467842 0.0005247 ────────────────────────────────────────────────────────────────────────────────────────────────────
Как видим, прямой эффект составляет 0.095 и он не достигает принятого в психологическом сообществе уровня значимости, а 95%-й доверительный интервал для него при использовании стандартного метода составляет (-0.063; 0.253), а полученный методом бутстрепа при 1000 повторений составил (-0.031; 0.279) – при этом у читателя должен получиться похожий, но несколько другой результат, так как бутстреп каждый раз генерирует новые подвыборки. Косвенный эффект составляет 0.193, он может быть оценен как значимый (p=0.003), стандартно рассчитанный доверительный интервал для этого коэффициента составляет (0.064; 0.323), а метод бутстрепа при нашем расчете дал 95%-й доверительный интервал (0.076-0.349). То есть если бы этот косвенный эффект совпадал с теоретическим (в генеральной совокупности), в 95% случаев в исследовании мы получили бы значения, попадающие в этот интервал. Как говорилось в главе 5, напрямую это не доказывает «истинности» косвенного эффекта, но позволяет сориентироваться, основываясь на радиусе интервала и его отношении к нулю. В нашем случае доверительный интервал прямого эффекта накрывает собой ноль, а косвенного это неверно, что повышает нашу уверенность в косвенном эффекте, хотя и не доказывает его полностью.
Упражнение 10.3(23)j. Проведите анализ повторно, указав в бутстрепе 5000 и 10000 подвыборок, используя аргумент boostrap = 5000 или 10000 (в последнем случае приготовьтесь подождать) и сравните полученные радиусы доверительных интервалов косвенного эффекта.
Упражнение 10.3(24)j. Вернемся к примеру, в котором рассматривались психологические факторы, помогающих людям делать зарядку (упражнение 10.3(12) в файле HealthBehavior.sav.
Используя функцию medпроведите анализ, направленный на выявление прямого и косвенного (через медиатор-намерение Intention) эффекта воспринимаемого контроля (Control) на поведение (Behavior).
По результатам можно заключить о значимом как прямом (95%-й доверительный интервал при стандартном методе расчета (0.099; 0.334), p<0.001), так и косвенном эффектах (доверительный интервал (0.006; 0.171), p=0.035) воспринимаемого контроля, что согласуется с рисунком 10.3(11).
Замечание. В этом расширении косвенный эффект рассчитывается перемножением двух эффектов (независимая переменная – медиатор и медиатор – зависимая переменная). Этот способ считается достаточно точным, если медиатор и зависимая переменная представлены в численных шкалах. Если же медиатор выражен в бинарной шкале или зависимая переменная – это количество каких-либо объектов, полученных пересчетом (например, число повторных госпитализаций пациентов), то рекомендуется применять другие методы (так называемую причинную медиацию, causal mediation), техническая реализация которых есть в других статистических пакетах (например, R и Mplus).
>> следующий параграф>>
[1] Тем не менее, к значимостям, полученным из больших матриц корреляций, в редакциях ведущих журналов отношение достаточно критическое.
[2] Скорректированный R2 ниже, поскольку независимых переменных в модели довольно много; он составляет 40.6%.
[3] Часто, поняв это, психологи задают следующий вопрос: зачем она тогда нужна? Существует два пути использования статистических методов в науках: описательный и объяснительный. Первый случай более «честный» с точки зрения математики — мы ищем модель, наилучшим образом описывающую полученные («реальные») данные, но не считаем, что эта модель — истина. Важно лишь то, что эта модель позволяет нам делать — например, в экономике мы можем надежно предсказать нечто на основе серии индикаторов, и нам не важно, как именно эти индикаторы «работают». Для психологии чаще важен второй случай — мы пытаемся привлечь статистику для «объяснения» реальности, для проверки того, «работает» ли наша теория. Такое использование статистики уязвимо для критики. Оно возможно, только если теория и дизайн исследования (например, эксперимент) позволяют исследователю обосновать (но все равно не доказать окончательно) свои выводы.
[4] Ajzen, I. (2001). Construction of a standard questionnaire for the theory of planned behavior.
[5] Это модельный пример, поэтому связи намеренно преувеличены
[6] В результате половина данных стала нулями — однако, эта потерянная информация будет учтена в модели благодаря переменной lookingtime_centered.
[7] По умолчанию функция corr.test выводит в консоль результат, округленный до двух знаков после запятой. Это можно регулировать, используя функцию print с опцией digits, например, для получения округления до трех знаков после запятой можно использовать конструкцию print(corr.test(data_workProd), digits = 3).