Непараметрические критерии предъявляют к используемым шкалам и распределениям переменных более низкие требования, чем аналогичные параметрические критерии, что в некоторых случаях делает их применение предпочтительным. В данной главе мы сосредоточимся на оценках значимости результатов. Доверительные интервалы для непараметрических методов имеют тот же смысл, что и в рассмотренных выше параметрических методах, но довольно сложные алгоритмы их построения мы здесь приводить не будем.
11.1.1. Критерий знаковых рангов Вилкоксона
Критерий знаковых рангов Вилкоксона используется в тех же ситуациях повторных измерений, что и соответствующий Т-критерий. В отличие от последнего, критерий Вилкоксона применим и в ситуациях, когда распределения не являются нормальными, однако данные должны быть измерены в интервальной шкале, поскольку сравниваются разности значений, принадлежащих разным участкам шкал.
Пример 11.1.1(1). Пусть наша выборка состоит из n чисел \( (x_1,x_2, \dots,x_n) \), которые являются разностями между двумя тестовыми результатами каждого испытуемого по тесту оптимизма до и после тренинга. Для критерия знаковых рангов формулировка гипотезы \( H_0 \) такова: эти числа являются результатом случайных колебаний показателя оптимизма симметрично в обе стороны вокруг нулевого значения[1] (тем самым математическое ожидание случайной величины, порождающей выборку, равно нулю, или — тренинг не оказывает систематического воздействия на уровень оптимизма участников).
Гипотеза \( H_1 \) утверждает, что есть тенденция к изменению уровня оптимизма и распределение показателя после тренинга отличается от распределения стартового замера некоторым положительным сдвигом.
Предположение о нормальности распределения не делается.
Пусть, например, разности между результатами второго и первого тестированием таковы: \( \{-3,-1,2,4,5,7,8,10,13,17\} \). Мы видим, что хотя уровень оптимизма увеличился не у всех участников тренинга, но, во-первых, большинство участников стали более оптимистичными, а во-вторых, у «неудачников» тренинга уровень оптимизма изменился слабее, чем у выигравшего от тренинга большинства. Критерий Вилкоксона чувствителен именно к такой ситуации.
Для того чтобы применить критерий Вилкоксона к данной выборке, надо:
1) расположить все члены выборки в порядке возрастания абсолютной величины, подписать под ними их ранги[1]; в нашем примере это будет следующий порядок и ранги:
| -1 | 2 | -3 | 4 | 5 | 7 | 8 | 10 | 13 | 17 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
2) вычислить статистику Вилкоксона, для чего подсчитать сумму рангов, приписанных отрицательным членам выборки (в нашем случае эта сумма \( 1+3=4 \));
3) оценить «хвостовую» вероятность, соответствующую полученному результату расчета статистики. Последнюю операцию мы проделаем с помощью приведенной ниже таблицы распределения Вилкоксона (таблица 11.1.1(2)). Мы найдем соответствующие нашему объему выборки критериальные значения, и сравним с полученным значением статистики Вилкоксона, равным 4.
Таблица 11.1.1(2). Распределение Вилкоксона. Нижние граничные значения.
| n | одностороннее 1%
двухстороннее 2% |
одностороннее 2.5%
двухстороннее 5% |
одностороннее 5%
двухстороннее 10% |
| 5 | 1 | ||
| 6 | 1 | 2 | |
| 7 | 0 | 2 | 4 |
| 8 | 2 | 4 | 6 |
| 9 | 3 | 6 | 8 |
| 10 | 5 | 8 | 11 |
Полученное по нашей выборке значение статистики Вилкоксона оказывается меньше граничного значения для выборки объема 10 и уровня значимости 0.02, которое равно 5 (для двухсторонних границ; о возможности применения одностороннего критерия см. 7.1.5). Значимость результата (относительно гипотезы о равенстве нулю среднего выборочного) меньше 0.02.
Мы использовали нижние граничные значения, поэтому рассчитывали статистику, суммируя ранги отрицательных выборочных значений. Полностью эквивалентный результат мы получили бы, суммируя ранги положительных выборочных значений и сопоставляя результат с верхними граничными значениями. Обычно в таблицах для симметричных распределений (а распределение Вилкоксона именно таково) приводятся только нижние или только верхние граничные значения. С нижними границами сопоставляется меньшая сумма рангов, с верхними — бóльшая, которая должна при этом превосходить граничные значения.
В пункте 11.3.1 проведен расчет примера с помощью пакета SPSS. Мы рекомендуем, если это возможно, проделать упражнение 11.3.1(1) сразу после чтения данного раздела.
Замечание 11.1.1(3). Парные значения в непараметрических критериях. Если используемая в исследовании шкала дискретна, тем более если она имеет лишь небольшое количество значений, то при использовании критерия Вилкоксона и других непараметрических критериев может возникнуть проблема: если два или больше чисел в выборке равны между собой, то как присваиваются ранги в этом случае?
Предположим, мы имеем ряд \( \{1, 2, 2, 2, 2, 4, 5\} \). Правило присваивания рангов вполне естественное: группа двоек занимает места со второго по пятое, следующая четверка занимает шестое место. Всем двойкам присваивается ранг \( (2+3+4+5)/4=3.5 \), а четверке присваивается ранг, соответствующий ее месту в ряду, а именно 6.
При таком алгоритме присвоения рангов их сумма по всем членам ряда остается неизменной, зависящей только от того, сколько всего в ряду чисел, независимо от количества равных значений.
11.1.2. Критерий Манна-Уитни для независимых выборок
В параграфе 6.1.2 мы решали задачу сравнения средних значений двух выборок, используя Т-критерий, который требует, чтобы выборки были реализациями нормально распределенных случайных величин.
Если условие нормальности не гарантируется, тем более если измерения проведены не в интервальной, а в порядковой шкале, к тем же выборкам для решения той же задачи можно применить критерий Манна-Уитни. Требования к распределениям для этого критерия слабее (подробнее в параграфе 11.2). Для абсолютно корректного применения требуется, чтобы выборочные распределения были подобны (отличались только сдвигом), но эти распределения не обязаны быть нормальными.
Пример 11.1.2(1). Проверяется гипотеза о том, что у родственников пациентов с шизофренией чаще, чем в норме, наблюдаются искажения мышления, характерные для шизофрении (хотя и гораздо реже, чем у больных). У молодых родственников пациентов с шизофренией (первая группа) и у испытуемых, у которых таких родственников не было (вторая группа), оценивалось количество ошибок по типу искажения мышления при выполнении набора заданий патопсихологического обследования. Предполагалось, что у родственников больных выраженность искажения мышления выше, чем в контрольной группе. Результаты таковы:
\( \{10, 12, 14, 17, 18, 19, 20, 22, 25, 27\} \) (первая группа).
\( \{7, 8, 9, 11, 13, 15, 16, 21\} \) (вторая группа).
Статистика Манна-Уитни — это не формула, а алгоритм вычисления. Чтобы рассчитать эту статистику для наших выборок, надо сначала записать члены обеих выборок в порядке возрастания, помечая значения признаком группы (мы выделяем курсивом первую и жирным шрифтом вторую группы):
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 25, 27.
Если бы случайные величины, испытаниями которых получены выборки, имели совершенно одинаковое распределение (гипотеза \( H_0 \)), то «жирные» и «курсивные» числа перемешивались бы более или менее равномерно. Если же первая группа имеет систематически больший балл, то «курсивные» числа должны оказаться в основном правее «жирных» — как оно и оказывается в нашем случае. Теперь мы пересчитаем это преимущество в значимость наших данных относительно гипотезы \( H_0 \). Для этого мы должны рассчитать статистику.
Алгоритм расчета таков:
1) каждому числу из последовательности присваиваем ранг, который подписываем под соответствующим числом:
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 25 | 27 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
2) Теперь суммируем ранги отдельно для «курсивных» \( S_1 \) и «жирных» \( S_2 \) чисел. Получаем \( S_1=4+6+8+11+12+13+14+16+17+18=119 \), \( S_2=1+2+3+5+7+9+10+15=52 \). Мы видим, что первая группа имеет сумму большую, чем вторая. Но поскольку выборки могут иметь сильно различающиеся объемы, то судить о том, какая группа преобладает, надо по средним рангам. В данном случае они равны соответственно \( 11.9 \) и \( 6.5 \). Первая выборка располагается в ряду правее второй.
Значимости можно определять по таблицам распределения. Для каждой пары объемов выборок распределение будет свое, поэтому таблицы достаточно громоздкие и мы не будем их здесь приводить. SPSS укажет значимости в таблицах вывода. Как их понимать, мы разберем в подпараграфе 11.3.2.
Замечание 11.1.2(2). О расчете статистики. Имеется альтернативный способ расчета статистики Манна-Уитни через попарное сравнение членов выборок (каждого с каждым). Результаты отличаются зависящей от объемов выборок легко рассчитываемой константой[2]. Далее мы рассмотрим два обобщения критерия Манна-Уитни, первый из которых удобнее считать через ранги, а второй — через сравнения. В предыдущей таблице заменим нижнюю строку. Вместо рангов будем писать только для «жирных» чисел, сколько «курсивных» находится в ряду левее каждого из них.
| 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 25 | 27 |
| 0 | 0 | 0 | 1 | 2 | 3 | 3 | 7 |
Сумма чисел нижней строки и есть альтернативный результат. В нашем случае она равна 16. Для выборок, обозначенных \( \{x\} \) и \( \{y\} \), этот результат обозначается \( U_{xy} \). Если к \( U_{xy} \) прибавить \( 8(8+1)/2=36 \) (8 — объем второй, «жирной» выборки), то полученные \(52\) и дают сумму рангов «жирной» выборки, посчитанную первым способом. Почему сумма рангов отличается от \( U_{xy} \) на \( n(n+1)/2 \), где n — объем выборки \( \{y\} \), — это не слишком сложная комбинаторная задача, которую мы оставляем читателю.
11.1.3. Критерий Краскелла-Уоллиса для n независимых выборок
Критерий Краскелла-Уоллиса обобщает критерий Манна-Уитни точно так же, как однофакторный дисперсионный анализ обобщает Т-критерий для двух выборок. Рассмотрим пример, аналогичный использованному при сравнении регрессионного и дисперсионного анализа, но с другими числами, более удобными для непараметрических критериев.
Пример 11.1.3(1). Пусть уровень статистических знаний оценивался по стобалльной системе у студентов первого, второго и третьего курса. Результаты первокурсников \( x:\{5, 9, 15, 18, 19\} \), второкурсников \( y:\{11, 12, 17, 22, 23\} \), третьекурсников \( z:\{10, 16, 20, 24, 25\} \). Нас интересует, меняется ли уровень знаний в процессе обучения статистике.
Для читателей, уловивших основные идеи построения статистик, статистика Краскелла-Уоллиса будет выглядеть вполне естественным обобщением статистики Манна-Уитни. Все три выборки выстраиваются в один ряд:
5, 9, 10, 11, 12, 15, 16, 17, 18, 19, 20, 22, 23, 24, 25
(если групп больше, то и сортов написания цифр должно быть больше) и числам присваиваются ранги. Затем ранги суммируются отдельно для каждой группы и вычисляется средний для группы ранг \( \overline{R}_i \). Если между группами нет систематических различий, то средние ранги будут колебаться вокруг общего среднего для рангов, равного половине от общего объема выборок, в нашем случае \( 15/2=7.5 \). Рассматривается сумма квадратов отклонений: \( H=(\overline{R}_1-7.5)^2+(\overline{R}_2-7.5)^2+(\overline{R}_3-7.5)^2 \). Если она велика, это говорит в пользу наличия систематических (не случайных) различий между группами. Для небольших объемов групп распределение статистики рассчитывается для каждого случая отдельно, при увеличении объема групп распределение статистики можно аппроксимировать распределениями Фишера или Хи-квадрат.
Критерий Джонкхиера нацелен на более узкую задачу, чем критерий Краскелла-Уоллиса. Их отношения похожи на отношения регрессионного анализа к дисперсионному, о котором мы говорили в подпараграфе 9.2.1. В двух разных случаях: (1) если уровень знаний студентов устойчиво падает или (2) максимум знаний приходится на второй курс, а затем падает ниже уровня первого курса, критерий Краскелла-Уоллиса будет показывать результат в пользу отвержения гипотезы о равенстве средних. Любые перестановки групп не меняют значение статистики и значимость результата
Мы же имеем в нашей задаче вполне определенный порядок групп и вполне определенные ожидания, что интересующий нас показатель уровня знаний должен демонстрировать рост по мере увеличения стажа учебы в университете. Нечувствительность критерия к перестановкам групп выглядит в этом случае странно: мы хотим доказать, что уровень подготовки студентов растет, но критерий Краскелла-Уоллиса даст тот же самый ответ, если уровень, например, с той же скоростью падает.
Поскольку близкая к нулю значимость приписывается критерием Краскелла-Уоллиса результатам, нас не интересующим, значимость (как вероятность ошибки первого рода) будет включать вероятности этих ненужных событий, т.е. будет переоцениваться не в нашу пользу.
Ситуацию можно улучшить, если применить другой критерий, более точно выделяющий нужную нам альтернативу — гипотезу о росте знания в процессе обучения. Этим свойством обладает критерий Джонкхиера.
Расчет статистики Джонкхиера проведем на том же примере. Напомним, результаты студентов таковы: у первокурсников \( x:\{5, 9, 15, 18, 19\} \), у второкурсников \( y:\{11, 12, 17, 22, 23\} \), у третьекурсников \( z:\{10, 16, 20, 24, 25\} \). Вычисляются статистики Манна-Уитни для всех возможных пар (ставя справа данные курса с бóльшим номером): \( U_{xy},U_{yz},U_{xz} \). Затем они складываются и рассчитывается общая статистика превосходства правых групп (с бóльшим номером) над левыми (с меньшим номером). В нашем случае это \( 17+15+20=52 \). Результат сравнивается со средним значением для ситуации с совпадающими групповыми средними. При равенстве групповых средних в сравнении двух групп по пять испытуемых примерно в половине из 25 пар левое число будет больше правого, а в половине — наоборот, т.е. средний балл на одно сравнение групп 12.5. В нашем случае три сравнения дадут \( 12.5*3=37.5 \). Наше значение статистики \( 52 \) больше среднего, следовательно, имеется тенденция к монотонному росту.
Значимость результата определяется по соответствующему распределению. Мы рекомендуем сейчас, если возможно, выполнить упражнение 11.3.3(1). Отметим, что значимость нашего результата при использовании критерия Краскелла-Уоллиса равна \( 0.289 \), а критерий Джонкхиера дает \( 0.127 \). Преимущество последнего, как мы говорили, вытекает из его более узкой направленности на монотонное изменение показателя.
11.1.5. Коэффициент корреляции Спирмена
Коэффициент корреляции Пирсона (см. 9.1.1)предназначен для расчетов меры связи нормально распределенных случайных величин. Если наши данные имеют иное происхождение (в частности, если они принадлежат шкале порядка), то корректно использовать непараметрическую меру связи — коэффициент корреляции Спирмена.
Рассмотрим пример. Группа из четырех испытуемых провела эксперимент на время реакции (ВР) на слуховые и зрительные стимулы. Показатели представлены в таблице 11.1.5(1) (время измерено в миллисекундах).
Таблица 11.1.5(1). Время реакции на слуховые и зрительные стимулы у четверых испытуемых.
| Номер испытуемого | 1 | 2 | 3 | 4 |
| Среднее ВР на слуховые стимулы | 497 | 576 | 658 | 709 |
| Среднее ВР на зрительные стимулы | 547 | 454 | 745 | 516 |
Для того чтобы посчитать коэффициент корреляции Спирмена для этих данных, сначала надо заменить исходные выборочные данные на их ранги[1] в соответствующей выборке (в новой таблице эти ранги проставлены под соответствующими строками), затем для каждого испытуемого вычислить разность \( d_i \) рангов, затем посчитать квадраты разностей \( d_i^2 \) и, наконец сумму этих квадратов по всем испытуемым (таблица 11.1.5(2)).
Таблица 11.1.5(2). Ранги времени реакции
| Среднее ВР на слуховые стимулы | 497 | 576 | 658 | 709 |
| Ранги ВР на слуховые стимулы | 1 | 2 | 3 | 4 |
| Среднее ВР на зрительные стимулы | 447 | 554 | 745 | 526 |
| Ранги ВР на зрительные стимулы | 1 | 3 | 4 | 2 |
| Разности рангов | 0 | -1 | -1 | 2 |
| Квадраты разностей рангов | 0 | 1 | 1 | 4 |
Сумма квадратов \( S=d_1^2+d_2^2+d_3^2+d_4^2=0+1+1+4=6. \)
Теперь остается только вычислить окончательный результат по формуле
\[ \hat r=1-6⋅\frac{S}{n(n^2-1)}. \]
Подставляя в формулу \( S=6 \) и размер выборки \( n=4 \), получаем
\[ \hat r=1-\frac{36}{60}=0.4. \]
Если в выборке имеются равные значения, то им приписываются равные средние ранги, как мы это делали в случаях статистик Вилкоксона и Манна-Уитни. Однако в этом случае в формулу подсчета надо вводить поправки, о которых мы здесь говорить не будем[4].
Можно показать, что если в выборках нет совпадающих значений, то число лежит на отрезке \( [-1;+1] \), т.е. \( -1≤\hat r≤1 \).
Упражнение 11.1.5(3). Проверить, что для выборок \( x:\{1, 2, 3\}, y:\{1, 2, 3\} \) выборочный коэффициент корреляции Спирмена равен 1, а для выборок \( x:\{1, 2, 3\}, y:\{3, 2, 1\} \) и \( x:\{1, 2, 3, 4\}, y:\{4, 3, 2, 1\} \) коэффициент равен −1.
Коэффициент корреляции Спирмена имеет в общем тот же смысл, что и коэффициент Пирсона, но он «выдерживает» допустимые преобразования порядковых шкал. Вследствие этого одинаковые значения будут иметь посчитанные по Спирмену корреляции пар выборок, изображенных на рис. 11.1.5(4) (коэффициенты корреляции Пирсона будут для них различны), где слева (а) изображена линейная зависимость, а справа (б) квадратичная. Равенство объясняется тем, что возведенные в квадрат значения (если они положительны) располагаются в том же порядке друг относительно друга, что и исходные значения. Другой пример мы разберем в подпараграфе 11.3.4.
Таблицы квантилей распределения коэффициента корреляции Спирмена мы не будем здесь приводить. Статистические пакеты дают точную оценку значимости результата относительно гипотезы о равенстве нулю теоретического коэффициента корреляции.
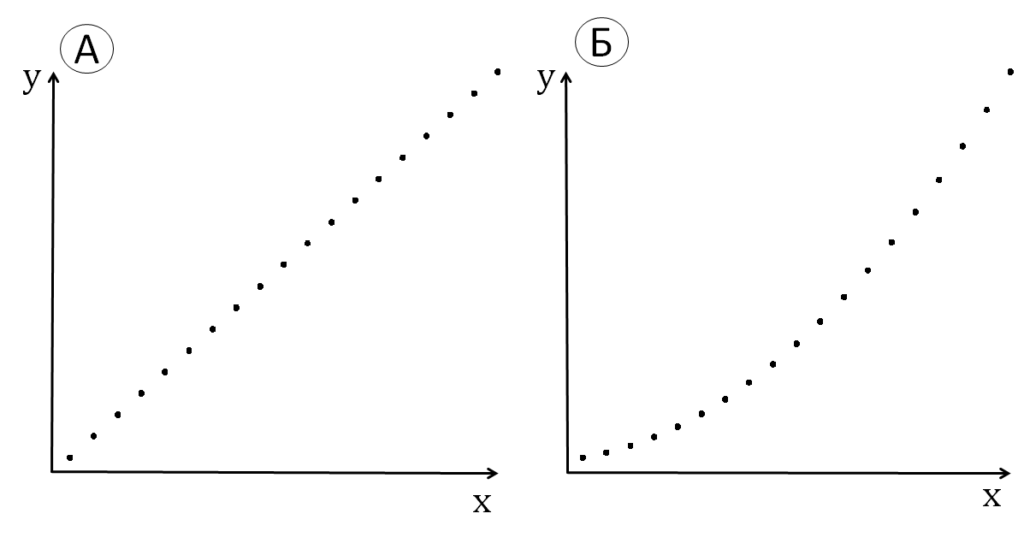Рис. 11.1.5(4). Выборки, связанные линейной и квадратичной зависимостью, которым соответствуют равные единице коэффициенты корреляции Спирмена
11.1.6. Таблицы сопряженности \( 2×2 \)
Таблицы сопряженности \( 2×2 \) дают самый грубый метод статистического оценивания связи переменных. Его преимущество — независимость от распределения переменных и хорошая наглядность. Кроме того, разобравшись с таблицами \( 2×2 \), мы получим основу для работы с таблицами более высоких порядков, которые используются для выявления нелинейных зависимостей.
Если сопоставляемые переменные дихотомические, т.е. имеют всего два значения (например, 1-«мужчина», 2 — «женщина» или 0 — «не согласен», 1 — «согласен»), то таблицы сопряженности \( 2×2 \) являются предпочтительным методом статистической обработки.
Пример 11.1.6(1). Эксперимент[5] был посвящен особенностям нарушения мышления у больных шизофренией. Одна из ключевых особенностей мышления при этом заболевании — нарушение избирательности внимания: больные в рассуждениях склонны опираться не на ведущие, основные признаки объектов, а на латентные, скрытые признаки предметов и явлений. Однако эти особенности могут помогать больным в тех случаях, когда нужно заметить и использовать не явное, а скрытое свойство предмета, — например, решить творческую задачу, требующую нестандартного подхода, им может быть легче, чем здоровым испытуемым.
Для проверки этой гипотезы и было проведено следующее исследование. Больным шизофренией и испытуемым контрольной группы предлагалось решить творческую задачу Л. Секея в варианте Л.И. Анцыферовой. Задача состояла в следующем. Испытуемым давали весы и несколько предметов (разновески, фонарик, баночка с солью, баночка с сухой ватой, карандаши, счетные палочки, ластик, свеча). Нужно было уравновесить весы таким образом, чтобы через некоторое время они сами вышли из равновесия. Единственное решение задачи состояло в том, чтобы сжечь свечу — по мере горения она теряет вес. Из 55 здоровых испытуемых самостоятельно решили задачу 25 человек, тогда как из 45 больных — 35. Данные запишем в таблицу:
Наблюдаемые частоты
| Не решил | Решил | Сумма | |
| Норма | 30 | 25 | 55 |
| Шизофрения | 10 | 35 | 45 |
| Сумма | 40 | 60 | 100 |
Отражённые в таблице результаты говорят в пользу того, что больные имеют преимущество при решении задачи. Наша задача — дать количественные меры этого преимущества.
Рассмотрим таблицу, в которой отражены только суммы: в эксперименте участвовали 55 здоровых и 45 больных, задачу не решили 40 и решили 60 человек:
Число испытуемых
| Не решил | Решил | Сумма | |
| Норма | 55 | ||
| Шизофрения | 45 | ||
| Сумма | 40 | 60 | 100 |
Что должно было бы оказаться в пустых клетках, если бы процент решивших и не решивших задачу был бы одинаков для больных и здоровых? Таблица, которая называется «таблица ожидаемых частот», выглядела бы так:
Ожидаемые частоты
| Не решил | Решил | Сумма | |
| Норма | 22 | 33 | 55 |
| Шизофрения | 18 | 27 | 45 |
| Сумма | 40 | 60 | 100 |
В гипотетической ситуации равных возможностей решения (гипотеза \( H_0 \)) задачу решили 60% как здоровых, так и больных. Автоматически пропорциональны доли здоровых (и больных) среди решивших и не решивших — по 55% и 45%.
Ожидаемые частоты получаются так: в верхней строке должно быть \( 55/100 \) участников, из них в левой верхней клетке \( 40/100 \). Тогда из 100 в левой верхней клетке должно оказаться \( 100⋅(55/100)⋅(40/100)=22 \) участника эксперимента. Аналогично для других клеток.
Следующая таблица отображает разности между наблюдаемыми и ожидаемыми частотами:
Разности наблюдаемых и ожидаемых частот
| Не решил | Решил | Сумма | |
| Норма | 8 | −8 | 0 |
| Шизофрения | −8 | 8 | 0 |
| Сумма | 0 | 0 | 0 |
Чтобы оценить значимость, делим квадраты значений в клетках таблицы разностей на значения в соответствующих клетках таблицы ожидаемых частот и суммируем результаты: \( : 8^2/22+(-8)^2/33+(-8)^2/18+8^2/27=2.91+1.94+3.56+2.37=10.78 \).
Если бы частоты соответствовали таблице ожидаемых частот, то результат проведенного расчета над случайной реализацией такой случайной величины имел бы распределение Хи-квадрат с одной степенью свободы. Полученные 10.78 — очень большое для такого распределения значение. Ему соответствует значимость 0.0011.
Замечание. В таблицах \( 2×2 \) на третьем этапе мы всегда получаем таблицу с равными по модулю значениями и одинаковыми знаками по диагонали (одна степень свободы). Это можно использовать для проверки.
Рекомендуем теперь, если это возможно, проделать упражнение 11.3.5(1).
11.1.7. Таблицы сопряженности более высоких размерностей
Таблицы сопряженности можно использовать для выявления более сложных отношений переменных, чем линейные зависимости.
Пример 11.1.7(1). В некотором банке проводится исследование уровня стресса у сотрудников в начале, середине и конце недели. Каждый раз обследуются 60 человек, выбираемых случайно из числа сотрудников банка:
| Начало | Середина | Конец | Сумма | |
| Низкий стресс | 15 | 0 | 15 | 30 |
| Средний стресс | 25 | 10 | 25 | 60 |
| Высокий стресс | 20 | 50 | 20 | 90 |
| Сумма | 60 | 60 | 60 | 180 |
Мы видим, что в середине недели доля сотрудников с высоким стрессом гораздо выше, чем в начале и конце. Для оценки значимости результата составим таблицу произведений долей. Для всех столбцов мы получаем равные доли: по 1/3 от общего числа испытуемых. По строкам: в первой строке 1/6 от общего количества испытуемых, во второй 1/3 и в третьей 1/2 от общего количества испытуемых.
Для \( H_0 \) о равенстве частот наблюдений уровня стресса по периодам недели таблица ожидаемого распределения испытуемых по клеткам такова[6]:
Таблица ожидаемых частот
| Начало | Середина | Конец | Сумма | |
| Низкий стресс | 10 | 10 | 10 | 30 |
| Средний стресс | 20 | 20 | 20 | 60 |
| Высокий стресс | 30 | 30 | 30 | 90 |
| Сумма | 60 | 60 | 60 | 180 |
Таблица разностей
| Начало | Середина | Конец | Сумма | |
| Низкий стресс | 5 | −10 | 5 | 0 |
| Средний стресс | 5 | −10 | 5 | 0 |
| Высокий стресс | −10 | 20 | −10 | 0 |
| Сумма | 0 | 0 | 0 | 0 |
Заметим, что таблица разностей для размеров больших, чем \( 2×2 \) не имеет такой простой структуры, как в случае \( 2×2 \). Для контроля можно использовать равенство нулю сумм по строкам и столбцам.
Далее проделаем знакомую по предыдущему примеру операцию — сложим квадраты разностей, деленные на содержимое клеток таблицы ожидаемых частот. Сумма такова:
\[ \frac{5^2}{10}+\frac{(-10)^2}{10}+\frac{5^2}{10}+\frac{5^2}{20}+\frac{10^2}{20}+\frac{5^2}{20}+\frac{(-10)^2}{30}+\frac{20^2}{30}+\frac{(-10)^2}{30}=\frac{150}{10}+\frac{150}{20}+\frac{600}{30}=37.5. \].
Число степеней свободы распределения \( \chi^2 \) для таблицы размера \( n×m \) вычисляется по формуле \( (n-1)(m-1) \). В нашем случае оно равно 4.
37.5 — очень большое значение для \( \chi^2 \). Мы можем быть уверены, что уровень стресса сотрудников данного банка меняется в течение недели. Однако о том, как он меняется, таблицы сопряженности говорят так же недостаточно внятно, как и дисперсионный анализ. В последнем предусмотрены апостериорные сравнения для прояснения подробностей динамики средних. В таблицах сопряженности таких уточняющих опций нет, к сожалению. В нашем примере можно уверенно сказать, что в середине недели стресс максимален, а в начале и конце примерно одинаков (это последнее утверждение о сходстве вообще невозможно подтвердить статистически). При других конфигурациях может быть достаточно трудно сформулировать гипотезу, которую таблица сопряженности подтверждает.
Например, такой вариант таблицы:
| Начало | Середина | Конец | Сумма | |
| Низкий стресс | 18 | 0 | 12 | 30 |
| Средний стресс | 25 | 10 | 25 | 60 |
| Высокий стресс | 17 | 50 | 23 | 90 |
| Сумма | 60 | 60 | 60 | 180 |
в целом также не согласуется с гипотезой о равенстве частот, однако это не позволяет сделать вывод о том, что имеется различие по уровню стресса в начале и конце недели. Если такой вывод нам интересен, придется проводить специально нацеленный на это эксперимент.
Упражнение 11.3.5(2), где разобран данный пример, можно выполнить сразу после чтения приведенного выше текста.
>> следующий параграф>>
[1] Ранги членов выборки — это их порядковые номера в ряду, где эти числа расставлены в порядке возрастания.
[2] Для симметричности распределения разностей достаточно того, что выборка состоит из разностей испытаний одинаково распределенных случайных величин. Условие не выполняется, например, если исходное распределение не симметрично, а распределение оптимизма после тренинга увеличивает дисперсию, т.е. «растягивает» распределение, сохраняя его общую картину.
[3] Этот способ расчета подробно описан в учебнике (Кричевец и др, 2003).
[4] Предлагаемые в отечественной литературе (например, Сидоренко, 2000; Рубцова, Леньков, 2005) формулы для поправок не совпадают с используемыми в пакете SPSS.
[5] Критская В.П., Мелешко Т.К. и Поляков Ю.Ф. Патология психической деятельности при шизофрении: мотивация, общение, познание. — М.: Изд-во МГУ, 1991.
[6] Напомним: в верхней левой клетке стоит произведение доли испытуемых в левом столбце, доли испытуемых в первой строке и общего количества испытуемых: \( 1/3⋅1/6⋅180=10 \); аналогично в других клетках.