4.2.1. Изменение единиц измерения
Плотность нормального распределения в общем случае задается следующей формулой
\[ f(x)=\frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-a)^2}{2\sigma^2}} \].
Мы говорили в подпараграфе 4.1.2, что график этой функции симметричен относительно вертикальной прямой \( x=a \), растянут по сравнению со стандартным в σ раз и во столько же раз сжат сверху вниз. Сейчас мы обсудим эти утверждения подробнее.
На графике рис. 4.1.3(3) видно, что математическое ожидание стандартной нормальной случайной величины является центром распределения и точкой максимума плотности. Предположим, что наша стандартная нормально распределенная случайная величина реализуется нами в игре в боулинг и отражает отклонение пущенного нами шара от центральной кегли, измеренное в дециметрах, причем отклонение влево будет отображаться отрицательными числами.
Упражнение 4.2.1(1). Какова вероятность того, что пущенный нами шар прокатится ближе, чем в дециметре от центральной кегли?
Решение. Эта вероятность равна площади заштрихованной фигуры на рис. 4.2.1(2). Правая половина этой фигуры (между нулем и единицей) имеет площадь, равную значению функции \( \Phi(x) \) при \( x=1 \). По таблице 4.1.3(2) находим, что \( Φ(1)=0.341 \), значит вероятность отклонения нашего шара меньше чем на дециметр равна \( 0.341⋅2=0.682 \).
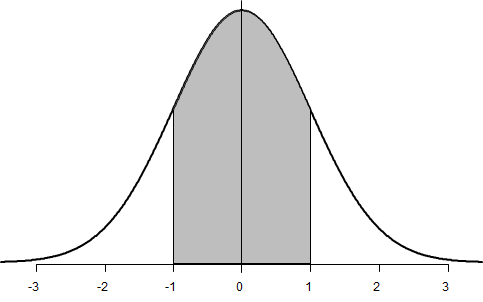Рис. 4.2.1(2). Вероятность, рассчитываемая как площадь фигуры под графиком плотности распределения.
Упражнение 4.2.1(3). Что произойдет с распределением, если отклонение мы будем измерять в готских дюймах (1 готский дюйм равен 5 см или 0.5 дм)?
Замена единиц измерения есть допустимое преобразование интервальной шкалы. Все значения исходной шкалы следует в нашем случае умножить на 2 (отметим, что уменьшение единицы измерения в 2 раза приводит к увеличению во столько же раз шкальных значений). Если на рис.4.2.1(4)а, на котором изображено стандартное нормальное распределение, описывающее отклонение нашего боулингового шара, просто заменить подписанные под осью абсцисс числа на вдвое большие, мы получим первый вариант решения. Однако если потребовать, чтобы единицы длины на графиках всегда отображались равными отрезками, то график придется растянуть в 2 раза вдоль оси абсцисс (рис. 4.2.1(4)б). Это, однако, приведет к тому, что площадь под графиком станет больше в 2 раза, а это для плотности распределения случайной величины недопустимо. Чтобы привести площадь к требуемой (равной единице) величине, просто сожмем график в 2 раза по оси ординат (рис. 4.2.1(4)в).
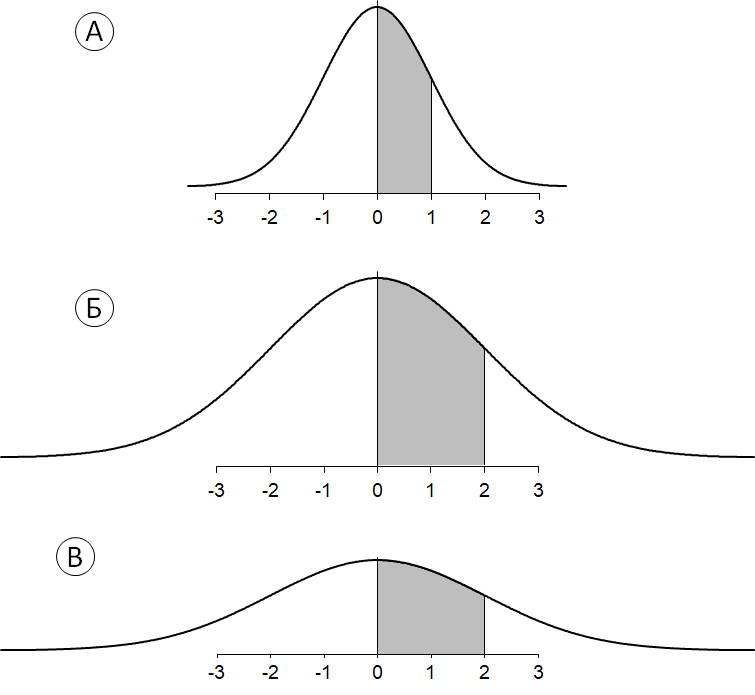Рис. 4.2.1(4). Уменьшение вдвое единицы измерения: поведение плотности распределения.
Нас теперь интересует уравнение, описывающее функцию, график которой дан на рис. 4.2.1(4)в, но сначала найдем, что надо поменять в формуле
\[ f(x)=\frac1{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \],
чтобы получить уравнение функции, график которой дан на рис. 4.2.1(4)б и представляет собой растянутый в два раза по горизонтали первый график. В точке \( x=2 \) вторая функция принимает такое значение, которое первая функция принимает при \( x=1 \) (это и есть суть операции растяжения в два раза). И более общо, при любом \(c\) в точке \( x=2c \) вторая функция принимает такое значение, которое первая функция принимает при \( x=c \). Именно такое соответствие значений обеспечивает формула
\[ f(x)=\frac1{\sqrt{2\pi}}e^{-\frac{(x/2)^2}{2}} \].
Действительно, подставив во вторую формулу \( x=2c \), мы получим такое же выражение, которое будет получено подстановкой \( x=1 \) в первую формулу.
Замечание. Эти рассуждения выглядят проще в самом общем виде. Пусть дана функция \( f(x) \). Будем обозначать через \( f(x/2) \) функцию, задаваемую правилом: «сначала поделить аргумент на 2, затем применить функцию f». Примерами таких функций могут служить пара \( sin(x), sin(x/2) \) или пара \( x^2;(x/2)^2 \). График функции \( f(x/2) \) будет представлять собой результат растяжения в два раза графика функции \( f(x) \). Доказательством является повторение вышеприведенного рассуждения: значения \( f(x) \) при \( x=c \) и \( f(x/2) \) при \( x=2c \) совпадают, а это и есть указанное растяжение.
Таким образом, график на рис. 4.2.1(4)б есть график функции
\[ f(x)=\frac1{\sqrt{2\pi}}e^{-\frac{(x/2)^2}{2}} \].
Совсем просто из этого следует, что график на рис. 4.2.1(4)в задается уравнением
\[ f(x)=\frac1{2\sqrt{2\pi}}e^{-\frac{(x/2)^2}{2}} \].
Аналогично разъясняется, что график функции \( f(x/σ) \) есть в \( σ \) раз растянутый график функции \( f(x) \), причем при «растянуть в \( σ \) раз» означает «сжать в \( 1/σ \) раз».
Это значит, что график функции
\[ f(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x/\sigma)^2}{2}}= \frac1{\sigma\sqrt{2\pi}}e^{-\frac{x^2}{2\sigma^2}} \].
есть растянутый в \( σ \) раз по горизонтали и одновременно сжатый в \( σ \) раз по вертикали график стандартного нормального распределения.
Отметим в дополнение, что заштрихованные на двух графиках рис. 4.2.1(4)а и 4.2.1(4)в фигуры имеют равные площади: вторая фигура получена из первой растягиванием в два раза по горизонтали с одновременным сжатием в два раза по вертикали.
4.2.2. Перенос начала координат
Перенос начала координат — это второе преобразование, которое нам понадобится. Предположим, мы решили отсчитывать расстояние не от центральной кегли, а от левой из тех, что расставлены на площадке. Допустим, она стоит левее центральной на 2 готских дюйма. Пересчитанные координаты подписаны под исходными на рис. 4.2.2(1) и выделены курсивом. Нас теперь интересует такая модификация формулы, чтобы она описывала график на рис. 4.2.2(1) в новой системе координат.
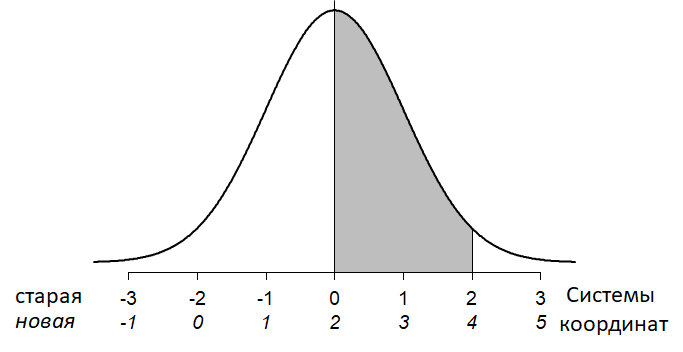Рис. 4.2.2(1). Сдвиг начала координат
Эта задача еще легче. На графике сразу видно, что функция принимает одинаковые значения для \( c \) в старой системе координат и для \( c+2 \) в новой, выделенной курсивом. Если для второй системы мы запишем формулу в виде
\[ f(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-2)^2}{2\sigma^2}} \].
то, глядя из начала этой новой системы координат, мы будем видеть график сдвинутым вправо на 2 единицы.
Аналогичным рассуждением мы можем получить, что при положительном \( a \) график функции
\[ f(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-a)^2}{2\sigma^2}} \]
получается сдвигом исходного графика вправо на \( a \) единиц, а график функции
\[ f(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x+a)^2}{2\sigma^2}} \].
получается сдвигом на столько же единиц влево.
Окончательно: график
\[ f(x)= \frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-a)^2}{2\sigma^2}}=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{((x-a)/\sigma)^2}{2}} \]
получается из графика стандартного нормального распределения растяжением по горизонтали в \( σ \) раз, сжатием во столько же раз по вертикали и сдвигом вправо на \( a \) единиц при положительном \( a \) и влево на \( |a| \) единиц, если \( a \) отрицательно.
Пусть случайная величина \( X \) имеет плотность распределения, заданную предыдущей общей формулой. Обратное преобразование шкалы \( x’=(x-a)/σ \), переведет график в график плотности стандартного нормального распределения (подставив x вместо \( x-a \), мы сдвинем график влево, а заменив \( x/σ \) на \( x \), сожмем его в \( σ \) раз, т.е. действительно проделаем обратные операции). Следовательно, операция над случайной величиной \( X’=(X-a)/\sigma \) даст в результате стандартную нормально распределенную случайную величину, график плотности которой задается знакомой нам формулой.