Пример 7.3(1). В файле EduCondition.sav содержатся данные примера подпараграфа 7.1.2. об условиях прослушивания некоторого курса студентами (факультатив, обязательный курс, отсутствие курса).
Отличие от данных, предназначенных для расчета Т-критерия, состоит в большем количестве групп. В данном случае группирующая переменная Condition принимает три значения.
Для проведения однофакторного дисперсионного анализа в SPSS необходимо вызвать в меню Анализ — Сравнение средних — Однофакторный дисперсионный анализ (Analyze — Compare means — One—way ANOVA). После этого на экране в возникшем диалоговом окне необходимо независимую переменную перенести в поле Фактор (Factor), а зависимую — в поле Список зависимых переменных (Dependent list)[1]. В нашем примере независимой переменной является группирующая переменная Condition[2], а зависимой — экзаменационная оценка Score.
Нажмем ОК, и в файле вывода получим основную таблицу 7.3(2), где указаны суммы квадратов, степени свободы и значение F, рассчитанные в подпараграфе 7.1.2, а также значимость результата:
Результаты однофакторного дисперсионного анализа в SPSS.
| Однофакторный дисперсионный анализ | |||||
| Score | |||||
| Сумма квадратов | ст. св. | Средний квадрат | F | Знч. | |
| Между группами | 6.000 | 2 | 3.000 | 1.500 | 0.296 |
| Внутри групп | 12.000 | 6 | 2.000 | ||
| Итого | 18.000 | 8 | |||
Пример 7.3(2). Откройте файл EduCondition2.sav, где находится второй вариант примера подпараграфа 7.1.2 (с удвоенной выборкой). Повторите выборы пунктов меню, описанные выше (кроме окончательного ОК).
При проведении дисперсионного анализа в SPSS можно также установить дополнительные параметры. В меню Параметры (Options) проставьте галочки в соответствующих квадратиках, чтобы
— задать вывод описательной статистики зависимых переменных по уровням фактора — пункт Описательные (Descriptive);
— задать вывод графика средних значений зависимой переменной на различных уровнях независимой переменной — пункт График средних (Means Plot);
— задать проверку равенства дисперсий у сравниваемых групп — пункт Проверка однородности дисперсий (Homogenity of variance test).
Выберите также пункт Апостериорные (Post hoc) и поставьте галочку в квадратик, помеченный Бонферрони (Bonferroni), который задает вид поправки для значимости при множественных сравнениях (см. 7.1.4).
После нажатия ОК перед основной таблицей мы получаем таблицу описательных статистик, где приводятся по каждой группе средние, стандартные отклонения, стандартные ошибки и доверительные интервалы для среднего. Она организована так же, как аналогичная таблица для Т-критерия. После нее выводится таблица с результатами теста однородности дисперсий Ливиня — также аналогичного употреблявшемуся в расчете Т-критерия. (О последствиях нарушения равенства дисперсий см. 6.2.2 и 11.2.3).
В основной таблице суммы квадратов и степени свободы изменились по сравнению с предыдущей версией примера.
Упражнение 7.3(3). Найдите и объясните изменения. В случае затруднения вернитесь к п. 7.1.2.
Таблицу 7.3(4), в которой приведены результаты апостериорных сравнений разберем подробнее.
Таблица 7.3(4). Результаты множественных сравнений в SPSS.
| Множественные сравнения | ||||||
| Зависимая переменная: Score
Бонферрони |
||||||
| (I) Condition | (J) Condition | Разность средних
(I−J) |
Стд. Ошибка | Знч. | 95% доверительный интервал | |
| Нижняя граница | Верхняя граница | |||||
| 1.00 | 2.00 | 1.00000 | 0.73030 | 0.573 | −0.9672 | 2.9672 |
| 3.00 | 2.00000* | 0.73030 | 0.046 | 0.0328 | 3.9672 | |
| 2.00 | 1.00 | −1.00000 | 0.73030 | 0.573 | −2.9672 | 0.9672 |
| 3.00 | 1.00000 | 0.73030 | 0.573 | −0.9672 | 2.9672 | |
| 3.00 | 1.00 | −2.00000* | 0.73030 | 0.046 | −3.9672 | −0.0328 |
| 2.00 | −1.00000 | 0.73030 | 0.573 | −2.9672 | 0.9672 | |
| * Разность средних значима на уровне 0.05. | ||||||
Первая строка значащей части таблицы показывает, что сравниваются первая и вторая группы, разность средних составляет единицу (т.е. среднее в первой группе на единицу больше среднего во второй), стандартная ошибка разности, которую получают усреднением стандартных ошибок по группам, с увеличивающей поправкой (в данном случае поправкой Бонферрони), затем поправленная значимость и поправленный доверительный интервал. Если значимость оказывается меньше 0.05, разность средних помечается звездочкой (в нашем случае помечены вторая и пятая строки, где сравниваются первая и третья группы). Остальные строки интерпретируются аналогично.
Наконец, после таблиц выводится график средних, понимание которого также не вызывает затруднений.
Апостериорные сравнения обычно, но не обязательно, вводятся в дело, когда дисперсионный анализ уже дал приемлемую значимость различий средних в целом по группам. Поправки учитывают количество сравнений, проводимых при множественном сравнении. В списке методов апостериорных сравнений, которые выводятся в соответствующем окне SPSS, предлагается 18 методов, в тонкости различий между которыми мы не будем здесь входить. Более подробную информацию о различных методах попарных сравнений можно найти, например, в книге «Дисперсионный анализ в экспериментальной психологии» А.Н. Гусева (Гусев, 2000).
Упражнение 7.3(5). Проведите сравнение первой и третьей групп с помощью Т-критерия и убедитесь, что апостериорные сравнения оценивают значимость различия как более слабую.
Пример 7.3(1)j. В файле EduCondition.sav содержатся данные примера подпараграфа 7.1.2. об условиях прослушивания некоторого курса студентами (факультатив, обязательный курс, отсутствие курса).
Отличие от данных, предназначенных для расчета Т-критерия, состоит в большем количестве групп. В данном случае группирующая переменная Condition принимает три значения.
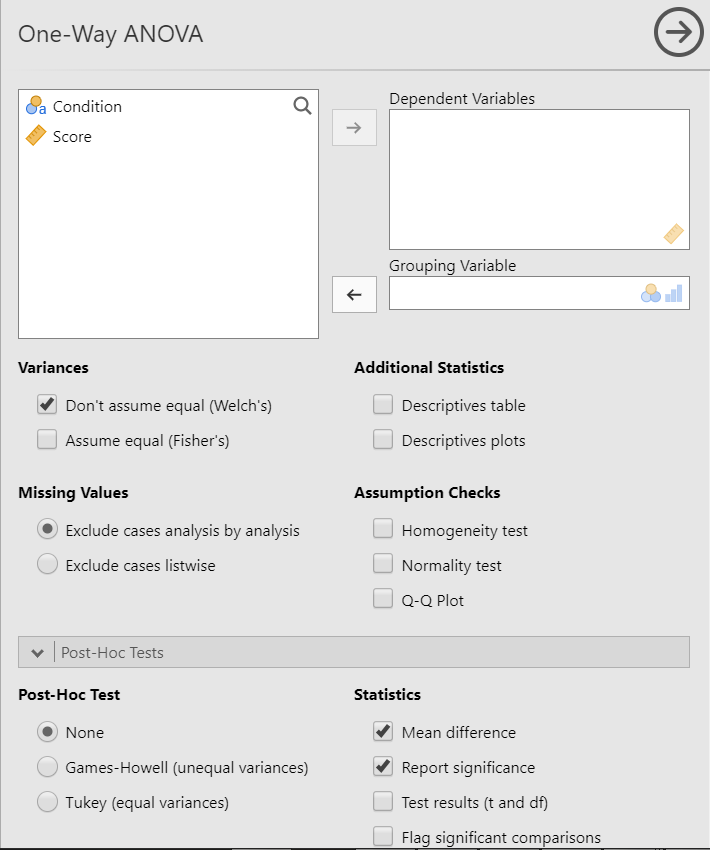
Для проведения однофакторного дисперсионного анализа в Jamovi необходимо вызвать в меню Analyses — ANOVA — One–Way ANOVA (ANOVA – сокращение от analysis of variance, английского названия дисперсионного анализа). После этого в появившемся окне анализа (рис. 7.3(2)j) надо независимую переменную перенести в поле Grouping variable, а зависимую — в поле Dependent variables). В нашем примере независимой переменной является группирующая переменная Condition, а зависимой — экзаменационная оценка Score.
Рис. 7.3(2)j. Диалоговое окно настройки дисперсионного анализа в Jamovi.
В Jamovi по умолчанию рассчитывается F-отношение с поправкой Уэлча (Welсh’s), предполагающую возможное неравенство дисперсий. Для того, чтобы получить точное значение F-отношения Фишера можно отметить в разделе Variances пункт Assume equal (Fisher’s).
После этого в окне результатов появится основная таблица 7.3(3)j указаны значение F, степени свободы и значимость, при этом F-отношение во второй строке (Fisher’s) совпадает с рассчитанным в подпараграфе 7.1.2. Из таблицы видно, что поправку Уэлча снижает значение F-отношения и, соответственно, его значимость (это происходит за счёт коррекции знаменателя в отношении и снижения числа степеней свободы, которые рассчитываются с учётом эмпирических значений стандартных отклонений в группе и поэтому могут оказываться дробными).
Таблица 7.3(3)j. Результаты однофакторного дисперсионного анализа в Jamovi.
| One-Way ANOVA | |||||||||||
| F | df1 | df2 | p | ||||||||
| Score | Welch’s | 1.276 | 2 | 3.789 | 0.377 | ||||||
| Fisher’s | 1.500 | 2 | 6 | 0.296 | |||||||
Из таблицы видно, что результат дисперсионного анализа в данном случае оказывается незначимым. Тем не менее, укажем на другие важные параметры, которые имеет смысл рассматривать при проведении дисперсионного анализа.
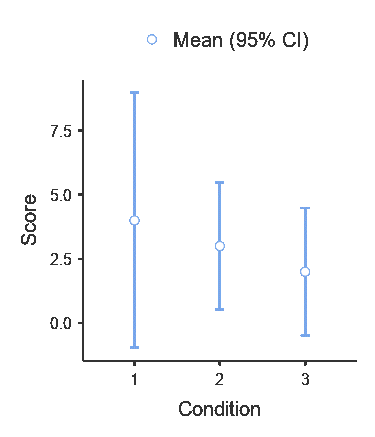
При проведении дисперсионного анализа в Jamovi имеет смысл также установить дополнительные параметры. В разделе Additional Statistics отметьте пункты Descriptives tables и Descriptives plots, что позволит рассчитать описательную статистику зависимых переменных по уровням фактора и вывести графики средних с доверительными интервалами (табл. 7.3.(4)j и рис. 7.3(5)j соответственно).
Таблица 7.3(4)j. Описательная статистика зависимой переменной на разных уровнях фактора в дисперсионном анализе.
| Group Descriptives | |||||||||||
| Condition | N | Mean | SD | SE | |||||||
| Score | 1 | 3 | 4.000 | 2.000 | 1.155 | ||||||
| 2 | 3 | 3.000 | 1.000 | 0.577 | |||||||
| 3 | 3 | 2.000 | 1.000 | 0.577 | |||||||
Рис. 7.3(5)j. График групповых средних с 95% доверительным интервалом в дисперсионном анализе.
Из таблицы и рисунка видно, что в среднем максимальный балл наблюдается в первой группе (факультативные дополнительные занятия), а минимальный – в в третьей (отсутствие дополнительных занятий). Однако, различия между группами невелики (относительно оценки доверительного интервала среднего), что соответствует небольшому значению статистики дисперсионного анализа.
Также, чтобы выбрать более адекватную статистическую оценку F-отношения (Фишера и Уэлча) можно провести проверку равенства дисперсий у сравниваемых групп с помощью критерия Ливиня, отметив пункт Homogenity test. Полученный результат представлен в таблице 7.3(6)j.
Таблица 7.3(6)j. Результаты проверки равенства дисперсий с помощью критерия Ливиня.
| Homogeneity of Variances Test (Levene’s) | |||||||||
| F | df1 | df2 | p | ||||||
| Score | 0.667 | 2 | 6 | 0.548 | |||||
Так как в результате получено достаточно низкое значения статистики Ливиня и оно оценивается как незначимое (p=0.548), мы в данном случае не можем отвергнуть нулевую гипотезу о равенстве дисперсий внутри трех групп, что дает нам основание для использования в качестве основной статистики Фишера без поправки Уэлча (что делает оценку эффекта более сильной, но все равно незначимой).
Также укажем на возможность попарного сравнения групп испытуемых между собой с поправкой на множественные сравнения. Для этого надо раскрыть раздел Post—Hoc Tests и в нём выбрать один из двух вариантов поправок – предполагающую равенство дисперсий в группах поправку Тьюки (Tukey (equal variances)) или поправку Геймса-Хауэлла, допускающую неравенство внутригрупповых дисперсий (Games—Howell (unequal variances)). Так как в этом примере уже известно, что различия дисперсий в группах незначительны, поэтому можно выбрать менее «консервативный» (то есть дающий более значимый результат) критерий Тьюки. В полученной таблице (7.3(7)j) по столбцам и строкам расположены группы, а в ячейках – соответствующие парам разности средних оценки значимости этих различий. При желании можно вывести точную статистику t-критерия, используемого для парных сравнений и метить звёздочками значимые различия (пункты Test results (t and df) и Flag significant comparisons).
Таблица 7.3(7)j. Результаты попарных сравнений с поправкой Nm.rb.
| Tukey Post-Hoc Test – Score | |||||||||
| 1 | 2 | 3 | |||||||
| 1 | Mean difference | — | 1.000 | 2.000 | |||||
| p-value | — | 0.679 | 0.269 | ||||||
| 2 | Mean difference | — | 1.000 | ||||||
| p-value | — | 0.679 | |||||||
| 3 | Mean difference | — | |||||||
| p-value | — | ||||||||
Пример 7.3(8)j. Откройте файл EduCondition2.sav, где находится второй вариант примера подпараграфа 7.1.2 (с удвоенной выборкой). Повторите выборы пунктов меню, описанные выше, проанализируйте результаты. Обратите внимание, что в основной таблице F-отношение и степени свободы изменились по сравнению с предыдущей версией примера.
Упражнение 7.3(9)j. Найдите и объясните изменения. В случае затруднения вернитесь к п. 7.1.2.
Упражнение 7.3(10)j. Проанализируйте таблицу попарных сравнений групп с поправкой Тьюки и найдите две значимо отличающиеся друг от друга группы. Сохранится ли значимость этих различий при использовании более строгой поправки Геймса-Хоуэлла?
Пример 7.3(1)r. В файле EduCondition.sav содержатся данные примера подпараграфа 7.1.2. об успеваемости, измеренной в условных единицах (переменная Score) студентов в условиях прослушивания некоторого курса (факультатив, обязательный курс, отсутствие курса).
Отличие от данных, предназначенных для расчета Т-критерия, состоит в большем количестве групп. В данном случае группирующая переменная Condition принимает три значения.
Перед проведением дисперсионного анализа рассчитаем описательную статистику успеваемости в каждой из трех групп с помощью уже знакомой нам функции describeByиз пакета psych, указав формулу Score ~ Condition в качестве основного аргумента. Если загрузить данные в таблице data_edu, то команда будет выглядеть так:
library(foreign)
library(psych)
data_edu <- read.spss("EduCondition.sav", to.data.frame = T, reencode = "utf8")
describeBy(Score ~ Condition, data = data_edu)
Результат выполнения будет следующим:
Descriptive statistics by group Condition: Факультатив vars n mean sd median trimmed mad min max range skew kurtosis se X1 1 3 4 2 4 4 2.97 2 6 4 0 -2.33 1.15 ------------------------------------------------------------------------------------- Condition: Обязательные занятия vars n mean sd median trimmed mad min max range skew kurtosis se X1 1 3 3 1 3 3 1.48 2 4 2 0 -2.33 0.58 ------------------------------------------------------------------------------------- Condition: Нет занятий vars n mean sd median trimmed mad min max range skew kurtosis se X1 1 3 2 1 2 2 1.48 1 3 2 0 -2.33 0.58
Как видно из приведенных таблицы, средние значения в трех группах равны 4, 3 и 2, при стандартных отклонениях 2, 1 и 1 соответственно. Оценить существенность этих различий можно с помощью дисперсионного анализа, однако перед этим визуализируем описательную статистику используя функцию error.bars.by, которую мы уже использовали в предыдущей главе:
error.bars.by(Score ~ Condition, data = data_edu, bars = TRUE, ylim = c(0, 10), colors = c("grey40", "grey60", "grey80"), main = "Descriptive", xlab = "Conditions", ylab = "Scores")
В результате будет получен график, изображенный на рис. 7.3(2)r.
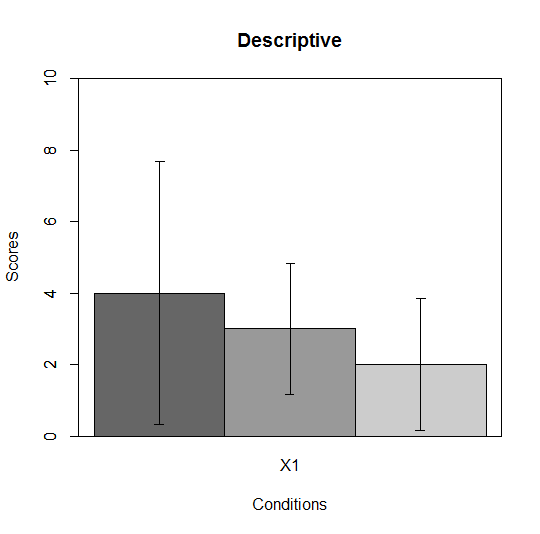 Рис. 7.3(2)r. График средних значений успеваемости в трех группах, построенный с помощью функции error.bars.by (столбики ошибок – 95% доверительный интервал среднего).
Рис. 7.3(2)r. График средних значений успеваемости в трех группах, построенный с помощью функции error.bars.by (столбики ошибок – 95% доверительный интервал среднего).
Замечание 7.3(3)r. В качестве альтернативы графики можно создавать также с помощью системы ggplot2, использующей так называемую The Grammar of Graphics (см. подробнее https://ggplot2.tidyverse.org/index.html). Для этого надо установить пакет ggplot2 с помощью функции install.packages. Затем надо сохранить описательную статистику по группам, рассчитанную с помощью функции describeByв табличном виде (указав дополнительный параметр mat=TRUE) в отдельную матрицу, которую можно назвать, например, descr_edu:
descr_edu <- describeBy(Score ~ Condition, data = data_edu, mat = T)
Переменная, обозначающая группу в этой таблице – group1 – рассчитывается как строковая, для построения графика лучше создать аналогичную переменную фактор, явно указав порядок групп (иначе они будут отсортированы по алфавиту). Это можно сделать, используя функцию factor и записав её результат в новую переменную group:
descr_edu$group <- factor(descr_edu$group1, levels = descr_edu$group1)
После этого можно построить график средних со столбиками ошибок, высота которых равна ±2 стандартных отклонения от средних. Для этого можно использовать следующую конструкцию:
library(ggplot2) ggplot(descr_edu, aes(x = group, y = mean)) + geom_col(fill="grey70") + geom_errorbar(aes(ymin = mean - se*2, ymax = mean + se*2), width=0.3) + labs(x = "Группа испытуемых", y = "Средний балл", title = "Успеваемость в трех группах", caption = "(столбики ошибок - 2*se)") + theme_light()
В первой строке указывается таблица данных, на основе которых строится график, затем в aes указаны переменные, которые соотносятся с осями x и y. Вторая строка указывает тип графика – столбиковая диаграмма (col от column). Далее в третьей строке на график добавлены столбики ошибок (errorbars), границами которых снизу указаны среднее — 2*стандартная ошибка среднего, а сверху – среднее + 2*стандартная ошибка среднего. Далее в функции labs заданные подписи по осям, заголовок и комментарий к графику и, наконец, в последней строке указан один из шаблонов оформления – light. Знаки “+” объединяют эти команды в одну конструкцию, такова логика системы ggplot. Результат выполнения этой команды изображен на рисунке 7.3(3)r.
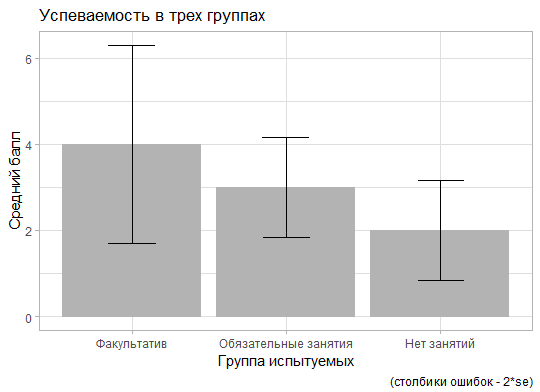 Рис. 7.3(4)r. График средних значений успеваемости в трех группах, построенный с помощью функции ggplot (столбики ошибок – 2 стандартные ошибки средних).
Рис. 7.3(4)r. График средних значений успеваемости в трех группах, построенный с помощью функции ggplot (столбики ошибок – 2 стандартные ошибки средних).
Теперь приступим к расчету дисперсионного анализа. Проведение дисперсионного анализа в R возможно различными способами, мы опишем самый базовый. Для этого можно использовать стандартную функцию aov(от analysis of variance), в которой надо указать формулу соотношения зависимой и независимой переменной, а также имя таблицы данных. Сохраним эту модель в переменную anova_edu и выведем результат с помощью функции summary:
anova_edu <- aov(Score ~ Condition, data = data_edu) summary(anova_edu)
Результат будет следующим[7]:
Df Sum Sq Mean Sq F value Pr(>F) Condition 2 6 3 1.5 0.296 Residuals 6 12 2
В полученной таблице 2 строки – Condition (по названию фактора) относится к межгрупповой дисперсии, а Residuals (остатки) – к внутригрупповой дисперсии. В столбце DF указаны степени свободы (Df от degree of freedom), затем – суммы квадратов (Sum Sq от Sum of Squares) и средний квадрат отклонений (Mean Sq от Mean Squares). Последние две строки содержать значение F-статистики (соотношение межгруппового среднего квадрата к внутригрупповому, 3/2=1.5) и оценка её значимости. Кратко результат дисперсионного анализа можно записать так: F(2, 6) = 1.5, p = 0.296. Как можно увидеть, результаты предсказуемо совпадают с рассчитанными подпараграфе 7.1.2.
При необходимости проверки равенства дисперсий у сравниваемых групп можно использовать уже описанную в предыдущей главе функцию leveneTestиз пакета car, которая рассчитывает тест Ливиня для оценки однородродности дисперсий:
library(car) leveneTest(Score ~ Condition, data = data_edu) Levene's Test for Homogeneity of Variance (center = median) Df F value Pr(>F) group 2 0.6667 0.5477 6
Как видно, в данном случае статистика Ливиня равна 0.6667, его значимость равна 0.5477, то есть в данном случае о существенном различии дисперсий говорить нельзя (о последствиях нарушения равенства дисперсий см. 6.2.2 и 11.2.3).
Ещё один важный вопрос – это попарное сравнение групп между собой. Так как в данном случае при сравнении трех групп между собой мы многократно тестируем гипотезу о равенстве средних, во избежание ошибки необходимо делать поправку на множественные сравнения. В R это можно сделать различными способами. Наиболее простой вариант – это использование функции pairwise.t.test, в которой надо указать в качестве первого аргумента зависимую переменную, в качестве второго аргумента – фактор, а затем – метод поправок на множественное сравнение. Например, рассчитаем значимость различий между тремя группами с поправкой Бонферрони:
pairwise.t.test(data_edu$Score, data_edu$Condition, p.adjust.method = "bonferroni")
Результат будет следующим:
Pairwise comparisons using t tests with pooled SD data: data_edu$Score and data_edu$Condition Факультатив Обязательные занятия Обязательные занятия 1.0 - Нет занятий 0.4 1.0 P value adjustment method: bonferroni
Ещё одна из наиболее распространенных поправок для множественных сравнений – это поправка или тест Тьюки (Tukey HSD от «honestly significant difference», см.: https://aaronschlegel.me/tukeys-test-post-hoc-analysis.html). Для её расчёта в R можно использовать функцию TukeyHSD, задав в качестве аргумента сохраненный в переменной результат дисперсионного анализа:
anova_edu <- aov(Score ~ Condition, data = data_edu) TukeyHSD(anova_edu) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = Score ~ Condition, data = data_edu) $Condition diff lwr upr p adj Обязательные занятия-Факультатив -1 -4.542938 2.542938 0.6792890 Нет занятий-Факультатив -2 -5.542938 1.542938 0.2693505 Нет занятий-Обязательные занятия -1 -4.542938 2.542938 0.6792890
Результат работы функции – таблица, в которой сравниваются все пары уровней фактора, в столбце diff выводятся разности средних сравниваемых групп, столбцы lwr и upr – нижняя и верхняя граница доверительного интервала разности соответственно, в p adj – оценка значимости отличия разности от нуля и поправкой на множественные сравнения.
Апостериорные сравнения обычно, но не обязательно, вводятся в дело, когда дисперсионный анализ уже дал приемлемую значимость различий средних в целом по группам. Поправки учитывают количество сравнений, проводимых при множественном сравнении. В R, помимо описанных методов, можно рассчитывать различные поправки, используя функцию p.adjust. Более подробную информацию о различных методах попарных сравнений можно найти в документации этой функции (https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/p.adjust), а также, например, в книге «Дисперсионный анализ в экспериментальной психологии» А.Н. Гусева (Гусев, 2000).
Пример 7.3(5)r. Откройте файл EduCondition2.sav, где находится второй вариант примера подпараграфа 7.1.2 (с удвоенной выборкой). Воспроизведите аналогичный анализ. Обратите внимание, что в основной таблице дисперсионного анализа, суммы квадратов и степени свободы изменились по сравнению с предыдущей версией примера.
Упражнение 7.3(6)r. Найдите и объясните изменения. В случае затруднения вернитесь к п. 7.1.2.
Упражнение 7.3(7)r. Проведите попарное сравнение групп, используя поправку Бонферрони и Тьюки. Проследите, насколько они изменились и какая поправка более «консервативна», то есть приводит к более сильному «штрафу» за множественное тестирование гипотез.
Упражнение 7.3(8)r. Проведите сравнение первой и третьей групп с помощью Т-критерия и убедитесь, что апостериорные сравнения оценивают значимость различия как более слабую.
Пример 7.3(6). Зависимость результатов дисперсионного анализа от внутригрупповой дисперсии.
Рассмотрим модельные результаты следующего эксперимента.
Исследовалось влияние просмотренного фильма на эмоциональное состояние испытуемых. Трем группам испытуемых были показаны три коротких видеоролика: первой группе демонстрировался небольшой научно-популярный фильм, второй группе — лирическая зарисовка на тему жизни в деревне, третьей — репортаж из криминальных новостей.
Исследование проводилось два раза: в одном случае испытуемые были обычные люди (данные в файле emotion1.sav, версия для SPSS, версия для Jamovi), во втором отбирались испытуемые с эмоциональной нестабильностью (данные в файле emotion2.sav, версия для SPSS, версия для Jamovi). Эмоциональное состояние измерялось с помощью методики самооценки эмоциональных состояний[3]. Два файла организованы одинаково: первый столбец содержит информацию о принадлежности испытуемого к одной из трех экспериментальных групп, второй столбец — результат проведения методики оценки эмоционального состояния, бóльшие баллы соответствуют лучшему эмоциональному состоянию.
Упражнение 7.3(7). Проведите дисперсионный анализ обоих файлов, выведя также описательные статистики. Сравните (внутригрупповые) стандартные отклонения в двух случаях, суммы квадратов и полученные в результате F-отношения. Сопоставьте средние по группам в двух случаях. Объясните различия самостоятельно, а затем проконтролируйте себя, прочитав ответ.
Ответ. В первом случае стандартное отклонение в каждой из трех групп равно 1.33, сумма квадратов ошибки равна 48, \( F(2,27)=22.5 (p < 0.001). \)
Во втором случае стандартное отклонение в каждой из групп равно 4.02 (в три раза больше, чем в первом), сумма квадратов ошибки равна 432 (в девять раз больше), \( F(2,27)=2.466 \) (в девять раз меньше, значимость ухудшилась: \( p=0.104 \)). Эмоционально нестабильные испытуемые дают больший разброс результатов измерений, поэтому эффект воздействия более «зашумлен» и труднее выделяется.
Исследовательский дизайн. Какие данные подходят для обработки дисперсионным анализом?
Приводимые далее примеры не сопровождаются файлами данных. В каждом случае прочитайте описание исследования. Вам далее предлагается
- Сформулировать гипотезу исследования.
- Обосновать, применим ли дисперсионный анализ для проверки гипотез данного типа.
- Выявить независимую и зависимую (зависимые) переменные. Определить, сколько уровней имеет независимая переменная.
Пример 7.3(8). В некотором вузе исследовался уровень самооценки студентов, обучающихся на различных факультетах. В исследовании принимали участие 4 группы студентов: учащиеся психологического, химического, математического и филологического факультетов. У всех этих испытуемых был измерен уровень самооценки с помощью стандартной методики Дембо-Рубинштейн в модификации Прихожан[4].
Конкретная (и самая очевидная) эмпирическая гипотеза, которую можно сформулировать в рамках такого исследования, может быть, например, такой: студенты, обучающиеся на различных факультетах, имеют различный уровень самооценки по шкалам «умный-глупый» и «способный-неспособный». Уровень самооценки в данной методике измеряется в баллах от 0 до 100, эти шкалы можно считать интервальными. Параметр «принадлежность к факультету» является независимой переменной или фактором, измеренным в шкале наименований.
Пример 7.3(9). Исследовалось влияние типа личностного расстройства на понимание эмоций других людей. В качестве испытуемых были отобраны здоровые люди, а также люди с истерическим расстройством и с шизоидным расстройством личности. Восприятие эмоций испытуемыми оценивалось с помощью опросника Н. Холла[5], по шкале «Распознавание эмоций других людей» (предполагаем, что шкала интервальная).
Пример 7.3(10). Исследовалось влияние конфликтов с родителями на уровень тревожности подростков. По частоте конфликтов подростков разделяли на тех, у кого практически не бывает конфликтов с родителями, тех, у кого они бывают иногда, и тех, кто конфликтует постоянно. Уровень тревожности оценивался при помощи опросника Спилбергера-Ханина (предполагаем, что шкала интервальная).
Пример 7.3(11). В стране N исследовалось, как влияет пол избирателей (мужчины в отличие от женщин) на их предпочтения на выборах президента (в президенты баллотировались три кандидата). Одной из переменных исследования был пол, указанный в анкете, а второй — кандидатура, за которую этот человек голосовал на выборах.
Пример 7.3(12). Множественное сравнение большого количества групп.
Целью данного задания является демонстрация неизбежности искажения оценки значимостей и, как следствие, ложных выводов при использовании множественных попарных сравнений независимых групп с помощью Т-критерия Стьюдента. В качестве основы для проведения статистического эксперимента в рамках данного задания следует использовать шаблон для генерации выборки случайных чисел, содержащийся в файле 20groups.sav. Файл уже содержит следующие данные: в столбце groups содержатся номера условных групп (20 групп по 50 «человек» в каждой), а в столбце test – случайно сгенерированные числа – экземпляры нормально распределенной случайной величины с математическим ожиданием 100 и стандартным отклонением 15. Далее мы предлагаем читателю самостоятельно сгенерировать такого рода данные и проверить, обнаружатся «значимые» различия между какой-нибудь парой групп.
Упражнение 7.3(13). Сначала следует сгенерировать данные для проведения анализа. Для этого необходимо в меню вызвать Преобразовать — Вычислить переменную (Transfom — Compute). В появившемся окне в качестве имени переменной следует указать test1, а в окне формулы расчета вставить функцию генерации нормально распределенной случайной величины с показателями среднего и стандартного отклонения 100 и 15 соответственно (в окне Группы функций (Group of function) выбрать Случайных чисел (Random numbers) и в появившемся ниже списке выбрать функцию RV.NORMAL и переместить ее в окно Числовое выражение (Numerical expression), где в образовавшиеся аргументные места (помеченные вопросительными знаками) вставить 100 и 15, чтобы получилось RV.NORMAL(100, 15)). После этого надо нажать ОК и подтвердить замену переменной. В столбце test появятся значения нормально распределенной случайной величины со средним значением 100 и стандартным отклонением 15. В первом столбце (переменная group) содержатся 20 групп, обозначенных числами от 1 до 20. Вместе с полученными случайными значениями это соответствует примерно следующей ситуации: мы измерили коэффициент интеллекта у пассажиров 20 вагонов метро (в каждом вагоне — по 50 человек).
После генерации выборки проведите однофакторный дисперсионный анализ с группирующей переменной group и зависимой test, задав опцию Описательные (Descriptives) в пункте Параметры (Options). В результате вы получите средние значения по всем 20 группам и общую оценку значимости результата. В нашем примере общая оценка значимости различий между средними значениями переменной test в 20 группах равна 0.628, а минимальное и максимальное значение среднего содержатся соответственно во второй и пятой группах.
Упражнение 7.3(13)j. Сначала следует сгенерировать данные для проведения анализа. Для этого необходимо в меню вызвать Data — Compute. В появившемся окне в качестве имени переменной (COMPUTED VARIABLE) следует указать test1, а в окне формулы расчета вставить функцию генерации нормально распределенной случайной величины с показателями среднего и стандартного отклонения 100 и 15 соответственно. Для этого можно вызвать список встроенных функций, нажав на кнопку fx, затем в разделе Simulation найти функцию NORM и вставить её в поле формулы вычисления двойным щелчком. Затем в скобках, через запятую, указать математическое ожидание (100 и стандартное отклонение (15), чтобы получилось NORM (100, 15) и нажать enter. В столбце test1 появятся значения нормально распределенной случайной величины со средним значением 100 и стандартным отклонением 15. В первом столбце (переменная group) содержатся 20 групп, обозначенных числами от 1 до 20. Вместе с полученными случайными значениями это соответствует примерно следующей ситуации: мы измерили коэффициент интеллекта у пассажиров 20 вагонов метро (в каждом вагоне — по 50 человек).
После генерации выборки проведите однофакторный дисперсионный анализ с группирующей переменной group и зависимой test, задав опцию Descriptives table в пункте Additional statistics. В результате вы получите средние значения по всем 20 группам и общую оценку значимости результата. В сгенерированных нами изначально данных (переменная test) общая оценка значимости различий между средними значениями переменной test в 20 группах равна 0.628, а минимальное и максимальное значение среднего содержатся соответственно во второй и пятой группах. В переменной test1 будет получена другая картина, оцените её.
Упражнение 7.3(13)r. После загрузки шаблона данных в таблицу данных следует сгенерировать данные для проведения анализа. В R для генерации выборки нормально распределенной случайной величины можно использовать функцию rnorm, указав три аргумента – объём выборки (n), среднее значение (mean, по умолчанию – 0) и стандартного отклонения (sd, по умолчанию – 1). В условиях, описанных выше, n = 1000, mean = 100, sd = 15. При генерации случайных данных получаемый результат уникален, однако, для воспроизведения одной и той же генерации многократно можно перед генерацией использовать функциюset.seed(x), где x – любое число, задающее стартовую позицию датчика случайных чисел. Для воспроизведения результатов, описанных ниже, надо использовать следующий скрипт:
data_20groups <- read.spss("20groups.sav", to.data.frame = T, reencode = "utf8")
set.seed(12321)
data_20groups$test <- rnorm(n = 1000, mean = 100, sd = 10)
Рассчитаем описательную статистику для полученной случайной выборки, используя функцию describeBy:
describeBy(data_20groups$test, data_20groups$groups, mat=TRUE, fast=TRUE, digits = 2) item group1 vars n mean sd min max range se X11 1 1 1 50 101.91 10.72 78.80 127.65 48.85 1.52 X12 2 2 1 50 101.75 9.35 77.15 119.60 42.45 1.32 X13 3 3 1 50 99.90 11.12 75.35 121.35 46.00 1.57 X14 4 4 1 50 98.92 10.14 71.86 117.95 46.09 1.43 X15 5 5 1 50 99.65 9.28 70.18 117.95 47.77 1.31 X16 6 6 1 50 102.26 8.77 84.39 120.72 36.33 1.24 X17 7 7 1 50 100.25 10.85 80.59 122.06 41.47 1.53 X18 8 8 1 50 101.19 9.60 77.29 122.39 45.09 1.36 X19 9 9 1 50 100.72 10.02 77.52 120.95 43.43 1.42 X110 10 10 1 50 101.97 8.86 75.57 126.34 50.77 1.25 X111 11 11 1 50 101.32 8.94 84.18 121.35 37.17 1.26 X112 12 12 1 50 97.56 9.40 75.10 115.44 40.34 1.33 X113 13 13 1 50 100.19 10.71 82.72 128.45 45.73 1.51 X114 14 14 1 50 100.92 10.41 82.36 127.13 44.77 1.47 X115 15 15 1 50 100.60 8.98 78.08 118.86 40.78 1.27 X116 16 16 1 50 98.67 9.25 77.52 128.72 51.19 1.31 X117 17 17 1 50 99.68 11.18 65.32 130.07 64.75 1.58 X118 18 18 1 50 101.05 9.99 79.50 118.82 39.32 1.41 X119 19 19 1 50 102.44 11.17 71.33 127.90 56.57 1.58 X120 20 20 1 50 98.80 10.08 72.51 122.39 49.88 1.43
Как видно, средние значения случайным образом колеблются вокруг теоретического среднего 100, это неизбежная вариативность выборочных оценок параметра распределения. Расчет дисперсионного анализа оценивает эту вариативность как неотличимую от случайного, F-отношение оказывается меньше единицы, общая оценка значимости различий между средними значениями переменной test в 20 группах равна 0.559:
summary(aov(test~groups, data= data_20groups)) Df Sum Sq Mean Sq F value Pr(>F) groups 19 1678 88.29 0.888 0.599 Residuals 980 97482 99.47
При этом, однако, если сравнить с помощью t-критерия, без поправок на множественные сравнения группы с минимальным и максимальным средним (это в нашей симуляции группы 12 и 19 соответственно), то значимость различий окажется достаточно близкой у нулю и ниже формальной границы 0.05:
t.test(data_20groups$test[data_20groups$groups == 12], data_20groups$test[data_20groups$groups == 19]) Welch Two Sample t-test data: data_20groups$test[data_20groups$groups == 12] and data_20groups$test[data_20groups$groups == 19] t = -2.3643, df = 95.201, p-value = 0.02009 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -8.9787677 -0.7826413 sample estimates: mean of x mean of y 97.5591 102.4398
Проведите попарное сравнение 20 групп между собой с поправкой Тьюки, используя функцию TukeyHSD. Убедитесь, что влияние фактора незначим (p=0.599). При попарном сравнении вы получите разность средних значении по всем 20 группам, найдите строку, соответствующую сравнению 12 и 19 группам, значимость различий оценивается на уровне p=0.625:
TukeyHSD(aov(test~groups, data= data_20groups))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = test ~ groups, data = data_20groups)
$groups
diff lwr upr p adj
<...>
19-12 4.88070450 -2.207802 11.969211 0.6255549
<...>
Если принять легенду с измерением интеллекта в вагонах метро, содержательно этот результат может быть ошибочно интерпретирован так: в пятом вагоне едут более умные люди, чем во втором.
Заметим в заключение: поскольку программы используют генератор псевдослучайных чисел, а не реально случайных (для наших целей разницы нет), то в первом эксперименте вы, вероятно, получите те же числа, что и мы (это характерно для SPSS). Если у вас остаются сомнения, повторите расчёт случайных значений (в R надо изменить число-аргумент в функции set.seed). Вы получите уже новые числа и сможете убедиться, что ошибка попарных сравнений снова воспроизвелась.
Пример 7.3(14). Расчет дисперсионного анализа для повторных измерений
Рассмотрим модельные результаты следующего эксперимента. Исследовалось влияние просмотренного фильма на эмоциональное состояние испытуемых. Группе испытуемых были показаны три коротких видеоролика: небольшой научно-популярный фильм, лирическая зарисовка на тему жизни в деревне и репортаж из криминальных новостей. Ролики демонстрировались с получасовым перерывом, при этом, чтобы избежать влияния порядка просмотра, порядок менялся так, что все возможные варианты последовательности просмотра встречались в выборке одинаково часто[8]. Эмоциональное состояние после просмотра роликов измерялось с помощью методики самооценки эмоциональных состояний[3], в этой шкале бóльшие баллы соответствуют лучшему эмоциональному состоянию. Исследователей интересовало, можно ли сказать, что самооценка эмоционального состояния меняется в зависимости от просмотра того или иного типа видеоролика. Модельные данные такого исследования представлены в файле emotion_films.sav (версия для SPSS, версия для Jamovi). Он содержит четыре переменные – id испытуемых и три оценки эмоционального состояния – после просмотра научно-популярного ролика, лирической зарисовки и криминального репортажа (переменные emotion_nonfiction, emotion_lyrics и emotion_crime соответственно. Так как в данном случае мы имеем дело с тремя связанными выборками, можно говорить о внутригрупповом факторе – тип просмотренного видео, и, соответственно, использовать дисперсионный анализ для повторных измерений. Рассмотрим, как можно провести этот анализ в разных статистических пакетах.
Для запуска дисперсионного анализа для повторных измерений в SPSS надо зайти в меню Анализ – Общая линейная модель – ОЛМ-повторные измерения (Analysis – General Linear Model – Repeated Measures). После вызова этого пункта появится окно настройки внутригруппового анализа, изображенное на рисунке 7.4(15).
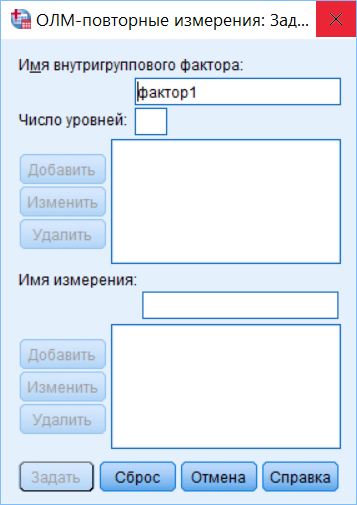
Рис. 7.3(15). Диалоговое окно настройки внутригрупповых факторов.
В нём надо указать название фактора (или факторов при многофакторном анализе) и число его/их уровней. Назовём фактор TypeOfVideo и укажем число уровней – 3, затем нажмём кнопку Добавить (Add) и затем Задать (Define), перейдя ко второму окну настройки анализа, изображенном на рис. 7.3(16).
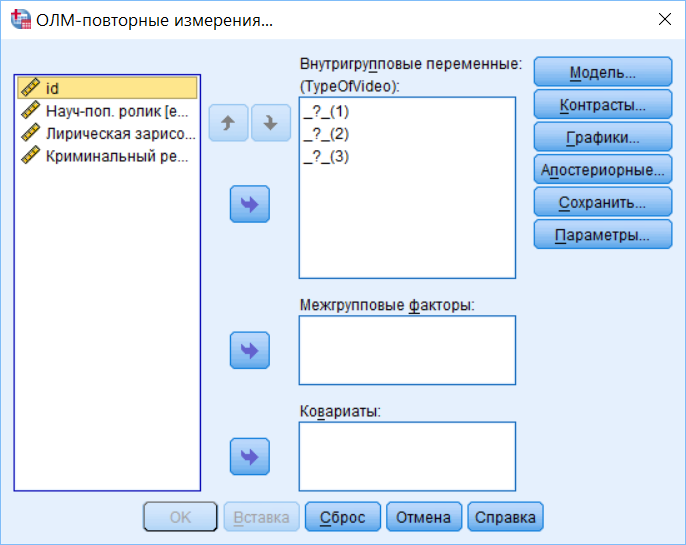
Рис. 7.3(16). Окно настройки дисперсионного анализа для повторных измерений.
В этом окне нужно указать внутригрупповые переменные – в нашем случае это emotion_nonfiction, emotion_lyrics и emotion_crime. Также имеет смысл вывести описательную статистику и величину статистического эффекта, зайдя в раздел Параметры (Options) и отметив пункты Описательные статистики (Descriptive statistics) и Оценка размера эффекта (Estimates of effect size). При желании, можно добавить графическое отображение соотношения средних, зайдя меню Графики (Plots), перенеся фактор TypeOfVideo в поле Горизонтальная ось (Horisontal Axis) и нажав кнопку Добавить (Add). В версиях SPSS начиная с 23 на графике средних можно отобразить столбики ошибок, мы рекомендуем это сделать, отметить пункт Включить столбцы ошибок (Include Error bars). После этого запустим анализ и рассмотрим результаты.
Первая содержательная таблица – это описательная статистика – средние значения и стандартные отклонения включенных в анализ переменных:
| Описательные статистики | |||
| Среднее | Стд. Отклонение | N | |
| Науч-поп. ролик | 34.5333 | 5.81160 | 30 |
| Лирическая зарисовка | 35.9000 | 3.22009 | 30 |
| Криминальный репортаж | 30.8667 | 8.81509 | 30 |
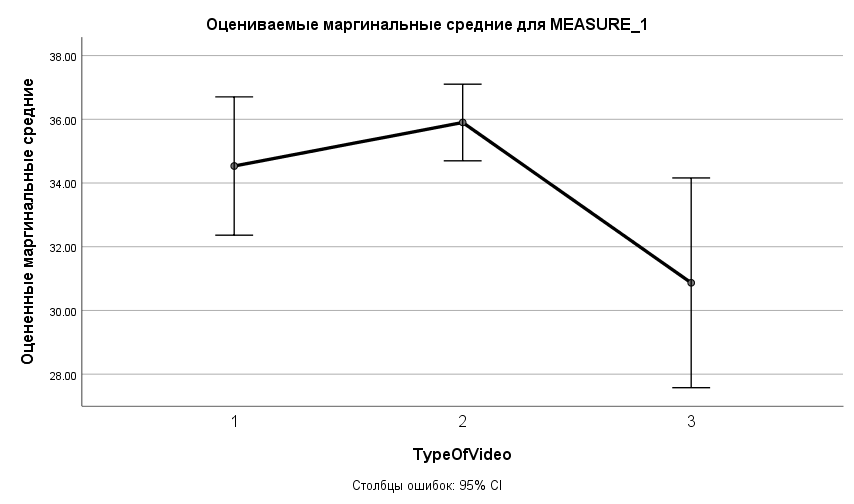
Можно заметить, что средние значения эмоционального состояния при просмотре научно-популярного ролика и лирической зарисовки отличаются несильно, а после просмотра криминального репортажа эмоциональное состояние заметно ниже. Можно обратить внимание, что стандартные отклонения заметно отличаются- оно особенно велико в случае просмотра криминального репортажа, что свидетельствует о большой вариативности реакции на такие видео. То же можно увидеть и на графике средних (рис. 7.3.17).
Рис. 7.1(17). Соотношение средних показателей эмоционального состояния после просмотра роликов разного типа.
Насколько существенно различие средних можно определить с помощью результатов дисперсионного анализа. В SPSS в начале приводятся результаты многомерного метода, о котором мы писали в Замечании 7.1(5):
| Многомерные критерииa | |||||||
| Эффект | Значения | F | Ст. св. гипотезы | Ст.св. ошибки | Знч. | Частная Эта в Квадрате | |
| TypeOfVideo | След Пиллая | .214 | 3.810b | 2.000 | 28.000 | .034 | .214 |
| Лямбда Уилкса | .786 | 3.810b | 2.000 | 28.000 | .034 | .214 | |
| След Хотеллинга | .272 | 3.810b | 2.000 | 28.000 | .034 | .214 | |
| Наибольший корень Роя | .272 | 3.810b | 2.000 | 28.000 | .034 | .214 | |
| a. План: Свободный член
Внутригрупповой план: TypeOfVideo |
|||||||
| b. Точная статистика | |||||||
В таблице приведены 4 варианта оценки влияния фактора, самый распространённый и устойчивый – это след Пиллаи, мы можем рекомендовать его в большинстве случаев (см., например: Ateş C. et al. Comparison of test statistics of nonnormal and unbalanced samples for multivariate analysis of variance in terms of type-I error rates //Computational and Mathematical Methods in Medicine, 2019). Как видно из таблицы, в данном случае все четыре метода дают одинаковый результат F(2, 28) = 3.810, p = 0.034, η2 = 0.214. Таким образом, влияние фактора может считаться значимы, при этом размер эффекта достаточно высок.
Следующая таблица содержит результат проверки сферичности распределения трех переменных:
| Критерий сферичности Моучлиa | |||||||
| Измерение: ИЗМЕРЕНИЕ-1 | |||||||
| Внутригрупповой эффект | W Моучли | Прибл. хи-квадрат | ст.св. | Знч. | Эпсилонb | ||
| Гринхауз-Гайссер | Юнха-Фельдта | Ограниченный снизу | |||||
| TypeOfVideo | .856 | 4.340 | 2 | .114 | .874 | .926 | .500 |
| Проверка нулевой гипотезы о том, что ковариационная матрица ошибок ортонормированного преобразования зависимых переменных пропорциональна единичной матрице. | |||||||
| a. План: Свободный член
Внутригрупповой план: TypeOfVideo |
|||||||
| b. Может использоваться, чтобы корректировать степени свободы для усредненных критериев значимости. Скорректированные критерии отображены в таблице Проверка внутригрупповых эффектов. | |||||||
Из неё видно, что тест Моучли оценивает отклонение от сферичности как незначимое, а значения коэффициента Эпсилон несильно отличается от единицы. Это может быть основанием для принятия допущения о сферичности данных, хотя небольшой размер выборки, как отмечалось в замечании 7.1.3(4), может приводить к недооценке несферичности данных. В следующей таблице приводится статистика одномерного дисперсионного анализа для повторных измерений, подробно рассмотренного в подпараграфе 7.1.3 – как без поправки, так и с поправками на несферичность (Четыре варианта оценки F-отношения отличаются числом степеней свободы – при поправке на несферичность они занижаются, в результате чего F-отношение оценивается как менее значимое):
| Проверка внутригрупповых эффектов | ||||||||
| Измерение: ИЗМЕРЕНИЕ-1 | ||||||||
| Иcточник | Сумма квадратов типа III | ст.св. | Средний квадрат | F | Знч. | Частная Эта в Квадрате | ||
| TypeOfVideo | Предполагая сферичность | 406.467 | 2 | 203.233 | 4.732 | .012 | .140 | |
| Гринхауз-Гайссер | 406.467 | 1.749 | 232.417 | 4.732 | .016 | .140 | ||
| Юнха-Фельдта | 406.467 | 1.852 | 219.488 | 4.732 | .015 | .140 | ||
| Ограниченный снизу | 406.467 | 1.000 | 406.467 | 4.732 | .038 | .140 | ||
| Ошибка(TypeOfVideo) | Предполагая сферичность | 2490.867 | 58 | 42.946 | ||||
| Гринхауз-Гайссер | 2490.867 | 50.717 | 49.113 | |||||
| Юнха-Фельдта | 2490.867 | 53.705 | 46.381 | |||||
| Ограниченный снизу | 2490.867 | 29.000 | 85.892 | |||||
Влияние фактора в предположении о сферичности оценивается как более значимое – F(2, 58) = 4.732, p = 0.012, с консервативной поправкой Гринхауз-Гайсера – как менее значимое – F(1.749, 50.717) = 4.732, p = 0.016, но даже с этой поправкой влияние эффект можно считать значимым. Величину эффекта можно считать средней (она оказывается ниже, чем при использовании многомерного подхода) – η2 = 0.140.
Также SPSS по умолчанию выводит ещё две таблицы, остановимся на них совсем кратко. Во-первых, это таблица Проверка внутригрупповых контрастов, в которой представлены результаты оценки различий между уровнями внутригруппового фактора. По умолчанию SPSS использует Полиномиальный (polynomial) метод оценки, при котором тренд изменения средних значений оценивается с мощью линейной и степенной (в нашем примере – квадртичной) модели:
| Проверка внутригрупповых контрастов | |||||||
| Измерение: ИЗМЕРЕНИЕ-1 | |||||||
| Иcточник | factor1 | Сумма квадратов типа III | ст.св. | Средний квадрат | F | Знч. | Частная Эта в Квадрате |
| factor1 | Линейный | 201.667 | 1 | 201.667 | 3.767 | .062 | .115 |
| Квадратичная регрессия | 204.800 | 1 | 204.800 | 6.328 | .018 | .179 | |
| Ошибка(factor1) | Линейный | 1552.333 | 29 | 53.529 | |||
| Квадратичная регрессия | 938.533 | 29 | 32.363 | ||||
Как видно из таблицы, конфигурацию средних в трех замерах лучше описывает не линейная, а квадратичная функция. В нашем случае это практически не имеет содержательной интерпретации, так как мы произвольно можем поменять уровни фактора и тогда этот результат изменится. Эта таблица может иметь смысл в том случае, когда внутригрупповой фактор представляет собой хотя бы порядковую или более сильную шкалу. Методы оценки контрастов можно менять в меню настройки анализа, в разделе Контрасты (Contrasts), подробное рассмотрение этой темы выходит за пределы нашего учебника, заинтересованного читателя мы можем адресовать к документации SPSS (https://www.ibm.com/docs/ru/spss-statistics/25.0.0?topic=contrasts-contrast-types).
Во-вторых, SPSS выводит таблицу Оценка эффектов межгрупповых факторов, в которой отражается эффект межгрупповых факторов, которые в нашем примере отсутствуют (например, мы могли бы различать две группы испытуемых – мужчин и женщин –и оценивать влияние и этого фактора, мы рассмотрим пример с межгрупповым фактором в следующей главе), поэтому таблица в данном случае не имеет содержательного смысла, она содержит только оценку отличия генерального среднего по всей выборке от нуля (которая ожидаемо значима). В следующей главе мы увидим, что добавление межгруппового фактора сделает эту таблицу более содержательной.
Таким образом, при использовании обоих подходов влияние фактора оказывается значимым, то есть можно говорить о неслучайном различии эмоционального состояния после просмотра разных типов видеороликов. Чтобы более подробно проанализировать это влияние можно использовать попарное сравнение с поправкой на множественное сравнение. В SPSS такое сравнение реализовано с поправкой Бонферрони. Для его расчета надо зайти в окно Параметры (Options), перенести фактор, по уровням которого требуется сделать попарные сравнения в окно Отобразить средние для (Compare Means for), отметить галочкой пункт Сравнить главные эффекты (Compare main effects) и выбрать поправку Бонферрони (Bonferroni) в выпадающем меню.
В результате в выводе появится следующая таблица:
| Парные сравнения | ||||||
| Измерение: ИЗМЕРЕНИЕ-1 | ||||||
| (I) factor1 | (J) factor1 | Разность средних (I-J) | Стд. Ошибка | Знч.b | 95% доверительный интервал для разностиb | |
| Нижняя граница | Верхняя граница | |||||
| 1 | 2 | -1.367 | 1.340 | .949 | -4.772 | 2.039 |
| 3 | 3.667 | 1.889 | .186 | -1.133 | 8.467 | |
| 2 | 1 | 1.367 | 1.340 | .949 | -2.039 | 4.772 |
| 3 | 5.033* | 1.796 | .027 | .471 | 9.596 | |
| 3 | 1 | -3.667 | 1.889 | .186 | -8.467 | 1.133 |
| 2 | -5.033* | 1.796 | .027 | -9.596 | -.471 | |
| На основе оцененных маргинальных средних | ||||||
| *. Разность средних значима на уровне .05. | ||||||
| b. Корректировка для множественных сравнений: Бонферрони. | ||||||
Оказывается, что значимо эмоциональное состояние отличается только после просмотра лирической зарисовки и криминального репортажа, остальные различия незначимы.
У читателя может возникнуть вопрос какой из методов – многомерный или одномерный использовать в своей работе? К сожалению, нет однозначного ответа, какой из подходов выбрать, но мы позволим дать себе следующую рекомендацию – лучше использовать одномерный вариант как более прозрачный с точки зрения механики вычислений, более мощный и более соответствующий идее повторных измерений, а многомерный метод использовать в случаях очень грубого нарушения сферичности распределения зависимых переменных.
Для запуска дисперсионного анализа для повторных измерений в Jamovi надо зайти в меню Analyses – ANOVA – Repeated Measures ANOVA). Откроется окно анализа, изображенное на рисунке 7.4(15)j.
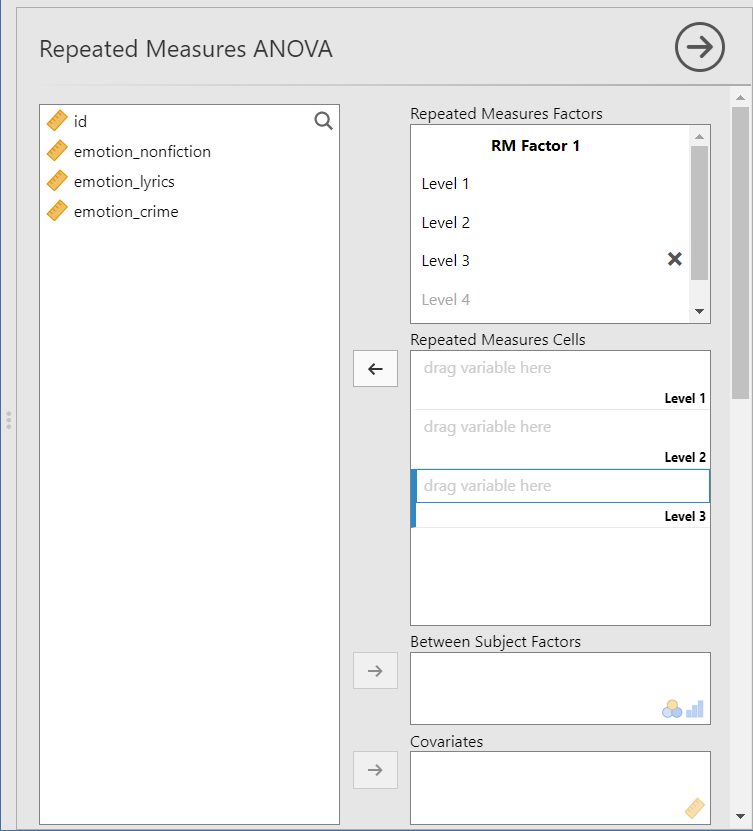
Рис. 7.3(15)j. Диалоговое окно дисперсионного анализа для повторных измерений.
В этом окне вначале в поле Repeated Measures Factors надо указать название фактора (или факторов при многофакторном анализе), а также число и названия его/их уровней. Назовём фактор Type Of Video и укажем уровни: pop-sci video, lyric sketch и criminal reportage. Затем в поле Repeated Measures Cells нужно указать внутригрупповые переменные – в нашем случае это emotion_nonfiction, emotion_lyrics и emotion_crime. Включим также расчет размера статистического эффекта, отметив пункт η2p. После этого появится основной результат дисперсионного анализа таблица внутригрупповых эффектов (Within Subjects Effects):
| Within Subjects Effects | |||||||||||||
| Sum of Squares | df | Mean Square | F | p | η²p | ||||||||
| Type Of Video | 406.467 | 2 | 203.233 | 4.732 | 0.0125 | 0.140 | |||||||
| Residual | 2490.867 | 58 | 42.946 | ||||||||||
| Note. Type 3 Sums of Squares | |||||||||||||
Из таблицы видно, что эффект оказывается значимым — – F(2, 58) = 4.732, p = 0.012. Величину эффекта можно считать средней – η2 = 0.140.
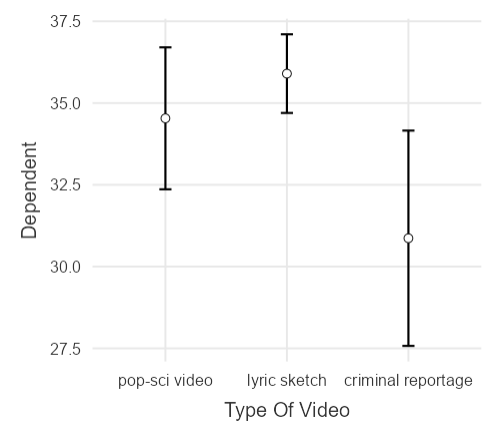
Для понимания того, как соотносятся средние оценок эмоционального состояния в трех экспериментальных условиях, в разделе Estimated Marginal Means (Оцененные групповые средние) можно перенести фактор в поле Term 1. По умолчанию выводится график средних с 95% доверительными интервалами, можно также вывести и таблицу с более точными значениями (пункт Marginal means tables). Из графика, изображенного на рисунке 7.1(16)j, видно, что средние значения эмоционального состояния при просмотре научно-популярного ролика и лирической зарисовки отличаются несильно, а после просмотра криминального репортажа эмоциональное состояние заметно ниже. Можно обратить внимание, что стандартные отклонения заметно отличаются- оно особенно велико в случае просмотра криминального репортажа, что свидетельствует о большой вариативности реакции на такие видео.
Рис. 7.1(16)j. Соотношение средних показателей эмоционального состояния после просмотра роликов разного типа.
Так как дисперсии в трех замерах отличаются, имеет смысл сделать тест на сферичность распределения зависимых переменных и, возможно, использовать поправки на несферичность. Для оценки сфериности отметим пункт Sphericity test (Тест сферичности) в разделе Assumption checks (Проверка допущений). После этого в выводе появится соответствующая таблица:
| Tests of Sphericity | |||||||||
| Mauchly’s W | p | Greenhouse-Geisser ε | Huynh-Feldt ε | ||||||
| Type Of Video | 0.856 | 0.1142 | 0.874 | 0.926 | |||||
Из неё видно, что тест Моучли оценивает отклонение от сферичности как незначимое, а значения коэффициента Эпсилон несильно отличается от единицы. Это может быть основанием для принятия допущения о сферичности данных, хотя небольшой размер выборки, как отмечалось в замечании 7.1.3(4), может приводить к недооценке несферичности данных. Выведем оценку F-отношения с поправками, отметив пункты Greenhouse-Geisser и Huynh-Feldt. В таблице Within Subjects Effects появятся две соответствующие строки, согласно которым F-отношение оценивается с консервативной поправкой Гринхауз-Гайсера – как менее значимое – F(1.749, 50.717) = 4.732, p = 0.016, но все равно, даже с поправкой влияние эффект можно считать значимым. Таким образом, можно говорить о неслучайном различии эмоционального состояния после просмотра разных типов видеороликов. Чтобы более подробно проанализировать это влияние можно использовать попарное сравнение – в разделе Post Hoc Tests перенесем в пустое поле фактор Type Of Video и отметим, помимо установленной по умолчанию поправки Тьюки поправку Бонферрони (Bonferroni). В выводе появится следующая таблица:
| Post Hoc Comparisons — Type Of Video | |||||||||||||||||
| Comparison | |||||||||||||||||
| Type Of Video | Type Of Video | Mean Difference | SE | df | t | ptukey | pbonferroni | ||||||||||
| pop-sci video | — | lyric sketch | -1.367 | 1.340 | 29.000 | -1.020 | 0.5707 | 0.9490 | |||||||||
| — | criminal reportage | 3.667 | 1.889 | 29.000 | 1.941 | 0.1454 | 0.1861 | ||||||||||
| lyric sketch | — | criminal reportage | 5.033 | 1.796 | 29.000 | 2.803 | 0.0235 | 0.0268 | |||||||||
Это дополнение показывает, что эмоциональное состояние значимо отличается только после просмотра лирической зарисовки и криминального репортажа, остальные различия незначимы.
Дисперсионный анализ для повторных измерений в R можно провести несколькими способами, как с помощью стандартной функции aov, таки используя функции различных пакетов, таких как ez и других.
В начале загрузим исходные данные и введем начало таблицы:
library(haven)
data_emotion <- read_spss("emotion_films.sav")
head(data_emotion)
id emotion_nonfiction emotion_lyrics emotion_crime
<dbl> <dbl> <dbl> <dbl>
1 1 36 38 30
2 2 37 33 15
3 3 42 41 35
4 4 24 39 25
5 5 38 41 28
6 6 27 32 30
Перед началом анализа оформленные таким образом даннные надо преобразовать данные в так называемый «длинный» формат (long format). В рассмотренных выше примерах обработки данных в SPSS и Jamovi традиционно используется «широкий» формат (wide format), при котором повторные измерения параметра у одного испытуемого размещаются в различные столбцы. В R для проведения дисперсионного анализа с повторными измерениями внутригрупповые замеры должны быть представлены не как отдельные переменные-столбцы, а как пара столбцов – собственно зависимая переменная и фактор, обозначающий номер или условие замера. В нашем случае это означает, что переменные emotion_nonfiction, emotion_lyrics и emotion_crime должны оказаться в одном столбце, назовём его, например, emotions, при этом надо создать новую переменную (назовём её typeOfVideo), который будет обозначать, к какому из замеров принадлежит каждая из строк. Такое преобразование в R удобно провести, используя функцию meltиз пакета reshape2 или gatherиз пакета tidyverse. Приведем оба варианта, дающих идентичные результаты.
При использовании функции melt надо в качестве аргументов указать таблицу данных, имя переменной, содержащей id испытуемых (id.vars = "id"), имя новой переменной, в которой будут сохранены повторные замеры – это аргумент value.name = "emotions"(по умолчанию –это все переменные, кроме id, но можно и прямо указать названия переменных в виде строкового вектора, используя аргумент measure.vars), им переменной, в которой будет сохранена информация о принадлежности значения зависимой переменной к замеру — variable.name = "TypeOfVideo"(это внутригрупповой фактор). Сохраним результата преобразования в новую таблицу data_emotion_long:
library(reshape2) data_emotion_long <- melt(data_emotion, id.vars = "id", value.name = "emotions", variable.name = "TypeOfVideo") head(data_emotion_long) id TypeOfVideo emotions 1 1 emotion_nonfiction 36 2 2 emotion_nonfiction 37 3 3 emotion_nonfiction 42 4 4 emotion_nonfiction 24 5 5 emotion_nonfiction 38 6 6 emotion_nonfiction 27
Другой вариант – это использовать функциюgather, используя пакет tidyverse и синтаксис pipeline. Передав исходную таблицу данных функции gatherукажем следующие аргументы: имя новой зависимой переменной value = "emotions", им внутригруппового фактора key = "TypeOfVideo", а также преобразуем его в фактор — factor_key = T, затем через запятую, без кавычек перечислим переменные повторных измерений. Это даст аналогичный предыдущему преобразованию результат:
library(tidyverse) data_emotion_long <- data_emotion %>% gather(key = "TypeOfVideo", value = "emotions", factor_key = T, emotion_nonfiction, emotion_lyrics, emotion_crime) head(data_emotion_long1) id TypeOfVideo emotions <dbl> <fct> <dbl> 1 1 emotion_nonfiction 36 2 2 emotion_nonfiction 37 3 3 emotion_nonfiction 42 4 4 emotion_nonfiction 24 5 5 emotion_nonfiction 38 6 6 emotion_nonfiction 27
Теперь перейдём к описательной статистике. Её можно рассчитать с помощью уже знакомой функции describeByиз пакета psych:
describeBy(emotions ~ TypeOfVideo, data = data_emotion_long, mat = T, digits = 3, fast = T) item group1 vars n mean sd min max range se emotions1 1 emotion_nonfiction 1 30 34.533 5.812 24 45 21 1.061 emotions2 2 emotion_lyrics 1 30 35.900 3.220 29 41 12 0.588 emotions3 3 emotion_crime 1 30 30.867 8.815 10 49 39 1.609
Можно заметить, что средние значения эмоционального состояния при просмотре научно-популярного ролика и лирической зарисовки отличаются несильно, а после просмотра криминального репортажа эмоциональное состояние заметно ниже. Можно обратить внимание, что стандартные отклонения заметно отличаются- оно особенно велико в случае просмотра криминального репортажа, что свидетельствует о большой. В примере 7.3(1)r описаны два варианта построения таких графиков с помощью функции из пакета psych или ggplot из пакета ggplot2, приведём оба варианта в данном примере:
library(psych)
error.bars.by(emotions ~ TypeOfVideo, data = data_emotion_long, bars = TRUE, ylim = c(0, 40), colors = c("grey40", "grey60", "grey80"), main = "Descriptive", xlab = "Conditions", ylab = "Emotion scores").
library(ggplot2)
descr_emo <- describeBy(emotions ~ TypeOfVideo, data = data_emotion_long, mat = T, digits = 3, fast = T)
descr_emo$group <- factor(descr_emo$group1, levels = descr_emo$group1, labels = c("Науч.-поп. видео", "Лирич. зарисовка", "Крим. репортаж"))
ggplot(descr_emo, aes(x = group, y = mean)) +
geom_col(fill="grey70") +
geom_errorbar(aes(ymin = mean - se*2, ymax = mean + se*2), width=0.3) +
labs(x = "Тип ролика", y = "Оценка эмоции", title = "Эмоциональное состояние после просмотра видео разного типа", caption = "(столбики ошибок - 2*se)") +
theme_light()
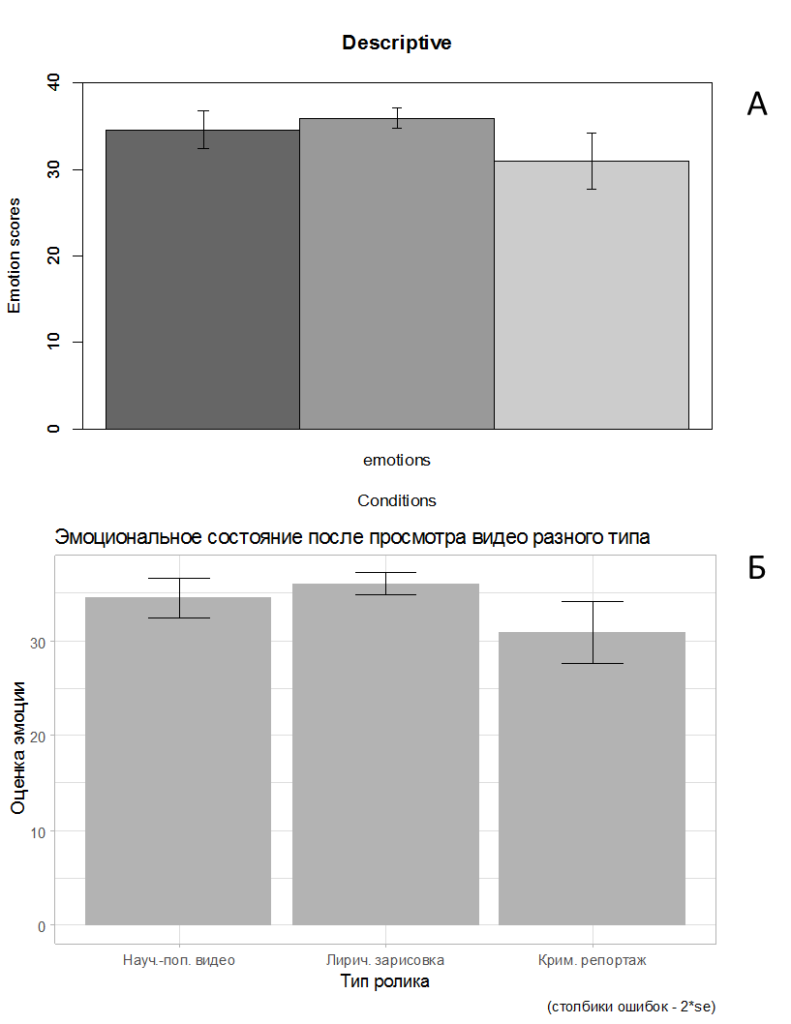 Рис. 7.1(17)r. Соотношение средних показателей эмоционального состояния после просмотра роликов разного типа, построенных с помошью пакетов psych (А) и ggplot2 (Б).
Рис. 7.1(17)r. Соотношение средних показателей эмоционального состояния после просмотра роликов разного типа, построенных с помошью пакетов psych (А) и ggplot2 (Б).
Насколько существенно различие средних можно определить с помощью результатов дисперсионного анализа. При использовании стандартной функции aov в случае повторных измерений надо указать в правой части формулы дополнительную составляющую Error, указывающую на источник дисперсии, связанной с межиндивидуальной дисперсией, при этом в качестве аргумента надо указать id испытуемых: Error(factor(id). Запишем результат анализа в переменную model:
model <- aov(emotions ~ TypeOfVideo + Error(factor(id)), data = data_emotion_long) model
В результате мы получим оценку влиянии фактора, полученного с помощью одномерного подхода, описанного в разделе 7.1.3:
Error: Within Df Sum Sq Mean Sq F value Pr(>F) TypeOfVideo 2 406.5 203.23 4.732 0.0125 * Residuals 58 2490.9 42.95 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 summary(model)
Из таблицы видно, что эффект оказывается значимым – F(2, 58) = 4.732, p = 0.012. Для расчета величины эффекта можно использовать функцию effectsize из одноименного пакета:
library(effectsize) effectsize(model) # Effect Size for ANOVA (Type I) Group | Parameter | Eta2 (partial) | 95% CI ---------------------------------------------------- Within | TypeOfVideo | 0.14 | [0.02, 1.00]
Величину эффекта можно считать средней – = 0.140.
Этот вариант расчёта с помощью базовой функции aov полезен для понимания устройства дисперсионного анализа, однако на практике более удобными и информативными могут быть другие функции. Остановимся на двух вариантах такого расширенного анализа.
Первый – это реализация дисперсионного анализа в пакете rstatix. В начале следует рассчитать модель с помощью функции anova_test, указав в аргументах набор данных data = data_emotion_long, зависимую переменную (dv – от dependent variavle) dv = emotions, переменную с уникальным идентификатором испытуемых wid = id и переменную, содержащую внутригрупповой фактор within = TypeOfVideo. Заметим, что при наличии межгруппового фактора его можно указать с помощью аргумента between. Также для оценки величины эффекта с помощью укажем аргумент effect.size = «pes» (pes – от partial eta-squared):
library(rstatix) res_aov <- anova_test(data = data_emotion_long, dv = emotions, wid = id, within = TypeOfVideo, effect.size = "pes")
Аналогичную модель можно описать с помощью формулу, которая для этой функции будет такова:
res_aov <- anova_test(data = data_emotion_long, emotions ~ TypeOfVideo + Error(id/ TypeOfVideo) , effect.size = "pes")
Результата анализа удобно посмотреть с помощью функции get_anova_table:
get_anova_table(res_aov)
ANOVA Table (type III tests)
Effect DFn DFd F p p<.05 pes
1 TypeOfVideo 2 58 4.732 0.012 * 0.14
Результат, естественно, совпадает с полученным выше. Однако, результаты содержат дополнительные результаты. Например, мы можем увидеть результаты проверки на сферичность и поправки, обратившись к элементам `Mauchly’s Test for Sphericity` и `Sphericity Corrections`:
res_aov$`Mauchly's Test for Sphericity`
Effect W p p<.05
1 TypeOfVideo 0.856 0.114
res_aov$`Sphericity Corrections`
Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF] p[HF]<.05
1 TypeOfVideo 0.874 1.75, 50.72 0.016 * 0.926 1.85, 53.7 0.015
По умолчанию функция get_anova_tableавтоматически вводит поправку Гринхауз-Гайсера (GG) при значимом результате теста Моучли. Пользователь может произвольно менять эту поправку с помощью аргумента correction, который может принимать значения «GG» (Greenhouse-Geisser), «HF» (Hyunh-Feldt), «none» (без коррекции) и «auto» (по умолчанию).
Чтобы более подробно проанализировать влияние фактора можно использовать попарное сравнение. Это можно сделать с помошью функции pairwise_t_testиз пакета rstatix, указав в аргументах набор данных, формулу, задающие зависимую и независимую переменные и тип поправки (наиболее распространенные –это поправка Бонферрони (bonferroni) и Хольма (holm)):
pairwise_t_test(data_emotion_long, emotions ~ TypeOfVideo, paired = T, p.adjust.method = "bonferroni") .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr> 1 emotions emotion_nonfiction emotion_lyr~ 30 30 -1.02 29 0.316 0.948 ns 2 emotions emotion_nonfiction emotion_cri~ 30 30 1.94 29 0.062 0.186 ns 3 emotions emotion_lyrics emotion_cri~ 30 30 2.80 29 0.009 0.027 *
pairwise_t_test(data_emotion_long, emotions ~ TypeOfVideo, paired = T, p.adjust.method = "holm") .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr> 1 emotions emotion_nonfiction emotion_lyr~ 30 30 -1.02 29 0.316 0.316 ns 2 emotions emotion_nonfiction emotion_cri~ 30 30 1.94 29 0.062 0.124 ns 3 emotions emotion_lyrics emotion_cri~ 30 30 2.80 29 0.009 0.027 *
Также можно использовать функцию tukey_hsd для расчета сравнений с поправкой Тьюки:
tukey_hsd(data_emotion_long, emotions ~ TypeOfVideo) term group1 group2 null.value estimate conf.low conf.high p.adj p.adj.signif * <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> 1 TypeOfVideo emotion_nonfi~ emoti~ 0 1.37 -2.56 5.29 0.685 ns 2 TypeOfVideo emotion_nonfi~ emoti~ 0 -3.67 -7.59 0.257 0.0721 ns 3 TypeOfVideo emotion_lyrics emoti~ 0 -5.03 -8.96 -1.11 0.00823 **
Как видно, при всех трех использованных попавках эмоциональное состояние значимо отличается только после просмотра лирической зарисовки и криминального репортажа.
В заключение опишем, как можно провести многомерный дисперсионный анализ в R. Это не очень просто, и мы предлагаем читателю решать самостоятельно – осваивать эту часть анализа или пропустить. В большинстве случаев описанного выше вполне достаточно.
Так как в многомерном подходе повторные замеры рассматриваются как отдельные переменные, в данном случае надо вернуться к исходному «широкому» формату.
В начале построим линейную модель, в которой будет оцениваться средних в трех замерах. Это можно сделать, указав в формуле модели справа матрицу из переменных повторных замеров, а справа – константу (1). Так как в исходных данных повторные замеры содержатся в столбцах со 2 по 4, то команда может быть следующей:
model_mult <- lm(as.matrix(data_emotion[,2:4])~1)
Убедимся, что результат содержит средние по трем переменным в качестве свободных членов и не содержит угловых коэффициентов:
model_mult Call: lm(formula = as.matrix(data_emotion[, 2:4]) ~ 1) Coefficients: emotion_nonfiction emotion_lyrics emotion_crime (Intercept) 34.53 35.90 30.87
Затем надо создать переменную-фактор, указывающую на уровни внутригруппового фактора. Это можно сделать, используя названия соответствующих столбцов исходной матрицы данных:
ifact <- factor(colnames(data_emotion[,2:4]))
Затем рассчитаем дисперсионный анализ, используя функцию Anova из пакета rstatix (не забудьте его загрузить, если не сделали этого раньше). При этом первый аргумент должен содержать модель, рассчитанную выше, затем в аргументе idata надо указать таблицу, содержащую уровни внутргрупповых факторов и в аргументе idesign – одностороннюю формулу, содержащую в правой части внутргрупповой фактор:
aov_mult <- Anova(model_mult, idata = data.frame(ifact), idesign = ~ ifact)
Результат будет достаточно обширным, для краткости мы оставим только существенное для нас:
summary(aov_mult)
Type III Repeated Measures MANOVA Tests:
------------------------------------------
<…>
Term: ifact
<…>
Multivariate Tests: ifact
Df test stat approx F num Df den Df Pr(>F)
Pillai 1 0.2139036 3.80952 2 28 0.034408 *
Wilks 1 0.7860964 3.80952 2 28 0.034408 *
Hotelling-Lawley 1 0.2721086 3.80952 2 28 0.034408 *
Roy 1 0.2721086 3.80952 2 28 0.034408 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
Sum Sq num Df Error SS den Df F value Pr(>F)
(Intercept) 102617 1 1042.8 29 2853.8408 < 2e-16 ***
ifact 406 2 2490.9 58 4.7323 0.01248 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Mauchly Tests for Sphericity
Test statistic p-value
ifact 0.8564 0.11415
Greenhouse-Geisser and Huynh-Feldt Corrections
for Departure from Sphericity
GG eps Pr(>F[GG])
ifact 0.87443 0.01649 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
F eps Pr(>F[HF])
ifact 0.9259434 0.0147043
В таблице Multivariate Tests: ifact содержатся интересующие нас результаты многомерного дисперсионного анализа, точнее — 4 варианта оценки влияния фактора, самый распространённый и устойчивый – это след Пиллаи (Pillai trace), мы можем рекомендовать его в большинстве случаев (см., например, Ateş C. et al. Comparison of test statistics of nonnormal and unbalanced samples for multivariate analysis of variance in terms of type-I error rates //Computational and Mathematical Methods in Medicine. – 2019). Как видно из таблицы, в данном случае все четыре метода дают одинаковый результат F(2, 28) = 3.810, p = 0.034. Дальше приводятся уже знакомые нам результаты одномерного дисперсионного анализа, оценки сферичности и поправки на несферичность.
У читателя может возникнуть вопрос какой из методов – многомерный или одномерный использовать в своей работе? К сожалению, нет однозначного ответа, какой из подходов выбрать, но мы позволим дать себе следующую рекомендацию – лучше использовать одномерный вариант как более прозрачный с точки зрения механики вычислений, более мощный и более соответствующий идее повторных измерений, а многомерный метод использовать в случаях очень грубого нарушения сферичности распределения зависимых переменных.
>> следующий параграф>>
[1] Если ввести в это поле несколько переменных, то в рамках одного дисперсионного анализа в SPSS можно проанализировать влияние фактора на несколько зависимых переменных. Однофакторный дисперсионный анализ можно провести также через пункты меню Анализ — Общая линейная модель — ОЛМ-одномерная (Analyze — General Linear Model — Univariate). Интерфейс этого варианта несколько отличается от варианта, который мы использовали. Возможность анализа нескольких зависимых переменных там не предусмотрена, но зато анализируется также сумма квадратов константы.
[2] В дисперсионном анализе порядковые и даже интервальные переменные в качестве независимых факторов рассматриваются только как именующие группы, т.е. как номинативные переменные.
[3] Сонин В.А. Психодиагностическое познание профессиональной деятельности. — СПб., 2004. С.94-96
[4] см., например, Прихожан А. М. Диагностика личностного развития детей подросткового возраста. — М.: АНО «ПЭБ», 2007.
[5] См., например, Фетискин Н.П., Козлов В.В., Мануйлов Г.М. Социально-психологическая диагностика развития личности и малых групп. — М., Изд-во Института Психотерапии. 2002. — C.57-59.
[6] Вообще говоря, мы не можем гарантировать, что вы получите значимость меньше 0.05. С очень маленькой вероятностью случайно вы можете получить и больший результат.
[7] Тот же результат можно получить, используя вложение функций друг в друга и, за счёт этого, сократив объём кода и не создавая промежуточных переменных: summary(aov(Score ~ Condition, data = data_edu))
[8] Обратите внимание, что в этом примере три уровня внутригруппового фактора не обязательно соответствуют хронологическому порядку замеров, это также возможный и достаточно часто встречающийся в психологических исследованиях случай.