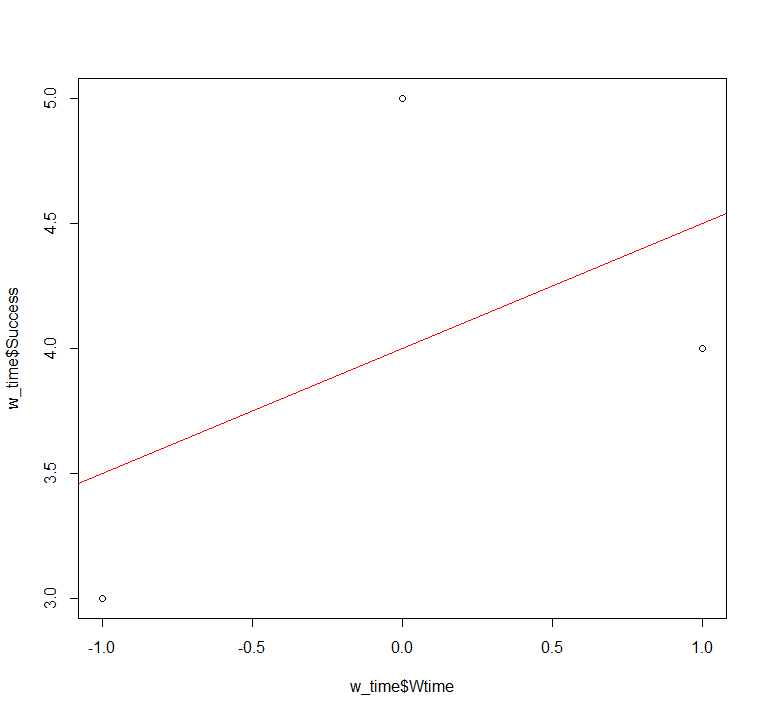Пример 9.3(1). Разложение сумм квадратов. Простейший пример
Рассмотрим простой пример, конкретизирующий пример подпараграфа 9.1.4. Предположим, ребенок А терпел и не брал конфету в течение 2 минут, а оценка его успехов во 2-м классе 3 балла; ребенок В терпел 3 минуты, а оценка его успехов 5 баллов; ребенок С терпел 4 минуты, а оценка его успехов 4 балла.
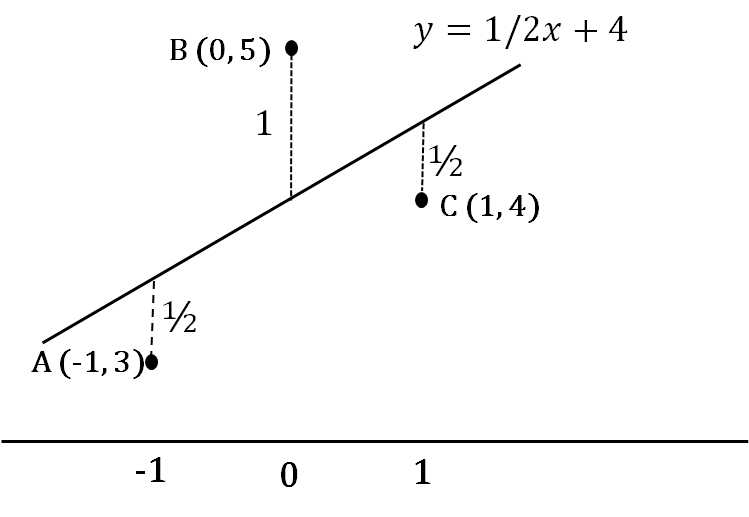
Для упрощения расчетов примем за нулевую точку среднее «время терпения» детей 3 минуты. В результате получаем три отображающих наши данные точки: (−1, 3), (0, 5) и (1, 4) — они изображены на рис. 9.3(2).
Рис.9.3(2). Регрессионная прямая для трех точек (−1, 3), (0, 5) и (1, 4).
Первый ребенок вытерпел на минуту меньше среднего значения, а третий на минуту дольше.
Среднее значение оценки успехов \( \overline{y}=4 \).
Обе наши выборки имеют дисперсию, равную единице, поэтому коэффициент ковариации равен коэффициенту корреляции \( COV_{xy}=r_{xy}=1/2 \). Напомним, что регрессионные коэффициенты рассчитываются по формуле:
\[ a=\frac{r_{xy}\cdot s_y}{s_x}, b=\overline{y}-\overline{x}\cdot a. \]
В нашем случае наилучшая в смысле суммы квадратов отклонений по оси y прямая имеет уравнение \( y=1/2\cdot x+4 \).
Составим суммы квадратов. Первая сумма \( S_{total} \) отражает дисперсию ординат наших точек, т.е. это сумма квадратов их отклонений от среднего (мы не делим ее и другие суммы на n − 1, поскольку будем рассматривать отношения сумм, как и в дисперсионном анализе): \( S_{total}=(3-4)^2+(5-4)^2+(4-4)^2=2 \) .
Вторая сумма \( S_{regression} \) [1] связана с собственно регрессионной моделью. Эта сумма квадратов отражает дисперсию предсказанных моделью значений. На рисунке 9.3(2) соответствующие точки лежат на регрессионной прямой и помечены звездочками. Подстановка x = −1 в регрессионное уравнение дает первую звездочку \( y=3\frac{1}{2} \) и остальные точки \( (0, 4) \) и \( (1,4\frac{1}{2}) \). Искомая сумма
\[ S_{regression}=(3\frac{1}{2}-4)^2+(4-4)^2+(4\frac{1}{2}-4)^2=\frac{1}{2}. \]
Третья сумма \( s_{residual} \) отражает ошибку регрессионной модели, то, насколько реальные наблюдения отклоняются от предсказанных. На рисунке отклонения изображены жирными линиями, соединяющими точки А, В, С с регрессионной прямой, их длины подписаны рядом с линиями \( S_{residual}=(\frac{1}{2})^2+(\frac{1}{2})^2+1^2=\frac{3}{2} \).
Читатель уже не удивится, обнаружив, что \( S_{total}=S_{regression}+S_{residual} \).
На каждую из сумм приходится по одной степени свободы, поэтому
\[ F_1^1=S_{regression}/S_{residual}=\frac{1}{3} \]
Можно добавить еще две суммы: сумму квадратов значений \( 3^2+4^2+5^2=50 \) и \( 4^2+4^2+4^2=48 \) и убедиться, что \( 50=48+S_{total} \). Но, как и в случае дисперсионного анализа, константа нас не интересует, когда мы ставим вопрос о связи переменных. Она нужна, только если мы хотим реально предсказывать значения.
Теперь посмотрим, как справляется с нашей задачей SPSS. Откроем файл Wtime.sav. Он содержит наши три наблюдения (переменные Wtime — «время терпения» и Success — «успеваемость во втором классе»). Сначала рассчитаем корреляцию между переменными.
Последовательно выберем пункты меню Анализ — Корреляции — Парные (Analyze — Correlation — Bivariate). В открывшемся окне переносим переменные Wtime и Success в поле Переменные (Variables). После нажатия ОК получаем таблицу.
| Корреляции | |||
| Wtime | Success | ||
| Wtime | Корреляция Пирсона | 1 | .500 |
| Знч.(2-сторон) | .667 | ||
| N | 3 | 3 | |
| Success | Корреляция Пирсона | .500 | 1 |
| Знч.(2-сторон) | .667 | ||
| N | 3 | 3 | |
Собственно корреляция между нашими переменными имеет величину 0.5, а соответствующая значимость равна 0.667.
Теперь проведем линейную регрессию. Выберем в меню пункты Анализ — Регрессия — Линейная (Analyze — Regression — Linear). В открывшемся окне перенесем переменную Success в окно Зависимая переменная (Dependent), а переменную Wtime в окно Независимые переменные (Independent(s)). Нажав ОК, получаем таблицы:
| Сводка для модели | ||||
| Модель | R | R-квадрат | Скорректированный R-квадрат | Стд. ошибка оценки |
| 1 | .500a | .250 | -.500 | 1.22474 |
| a. Предикторы: (конст) W_time | ||||
| Дисперсионный анализa | ||||||
| Модель | Сумма квадратов | ст.св. | Средний квадрат | F | Знч. | |
| 1 | Регрессия | .500 | 1 | .500 | .333 | .667b |
| Остаток | 1.500 | 1 | 1.500 | |||
| Всего | 2.000 | 2 | ||||
| a. Зависимая переменная: Success | ||||||
| b. Предикторы: (конст) W_time | ||||||
| Коэффициентыa | ||||||
| Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | t | Знч. | ||
| B | Стд. Ошибка | Бета | ||||
| 1 | (Константа) | 4.000 | .707 | 5.657 | .111 | |
| W_time | .500 | .866 | .500 | .577 | .667 | |
| a. Зависимая переменная: Success | ||||||
В первой таблице нам представлены коэффициент корреляции R и показатель качества модели R2 [2].
Во второй — рассчитанные нами выше суммы квадратов: регрессия (regression), остаток (residual), общая (total). Это те самые 0.5, 1.5 и 2, которые мы получили в расчетах предыдущего пункта. Далее с этими числами производятся операции, аналогичные тем, которые производились в дисперсионном анализе: суммы квадратов делятся на число степеней свободы (здесь они обе равны единице, в других примерах это будут другие числа), и затем 0.5 (регрессия) делится на 1.5 (остаток). Получается F-отношение 0.333, которому соответствует значимость 0.667 — та же самая, что и значимость корреляции, которую мы посчитали выше. Для простой линейной регрессии это всегда так.
В третьей таблице приведены регрессионные коэффициенты. В столбце, озаглавленном «B», первое число — это свободный член (в нашем случае, когда переменная Wtime центрирована, свободный член равен среднему по трем наблюдениям переменной Success), а второе число — угловой коэффициент регрессионного уравнения: 0.5.
В столбце, озаглавленном «Бета», даны регрессионные коэффициенты, как если бы уравнение составлялось после стандартизации переменных. Свободный член в этом случае равен всегда нулю и поэтому не приводится. Угловой коэффициент в нашем примере тот же самый, потому что дисперсии наших переменных равны единице и стандартизация бы их не изменила. В следующем примере мы получим различие стандартизованных и нестандартизованных коэффициентов. Далее, можно оценить значимость результата (т.е. рассчитанного регрессионного коэффициента) относительно нулевой гипотезы (регрессионный коэффициент равен нулю — т.е. успешность в школе не зависит линейно от времени ожидания) [3]. Для этого, деля нестандартизованный коэффициенты регрессии на его стандартную ошибку (\( 0.500/0.866=0.577 \)), получим показатель, сравнив который с t-распределением Стьюдента узнаем, какой хвост отсекают эти значения, или их значимость. В случае одной независимой переменной эти результаты совпадают с результатами дисперсионного анализа: F-отношение и t углового коэффициента связаны формулой \( F=t^2 \), а значимости одинаковы [4].
Чтобы графически представить полученный результат, построим диаграмму рассеяния для «времени выдержки» и успеваемости наших трех школьников: в меню Графика — Устаревшие диалоговые окна — Рассеяния/Точки (Graphs — Legacy Dialogs — Scatter/Dot) выбрать Простая диаграмма рассеяния (Simple Scatter) и перенести переменные в строки ось X и Y. Если дважды кликнуть по построенной диаграмме и выбрать в открывшемся окне в меню пункт Добавить: линия аппроксимации для итога (Add Fit Line at Total), регрессионная прямая добавится на рисунок.
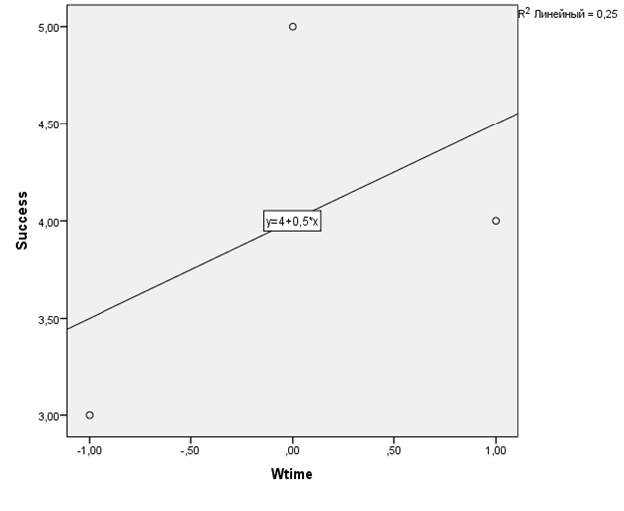Рис. 9.3(4). График рассеяния с линией регрессии для модели из трех точек
Заметим в заключение, что показатель R2 может быть получен как возведением в квадрат коэффициента корреляции, так и делением суммы регрессии (0.5) на общую сумму (2). Второй способ прямо связан с оценками моделей в других, более сложных случаях.
Теперь посмотрим, как справляется с нашей задачей Jamovi. Откроем файл Wtime.sav. Он содержит наши три наблюдения (переменные Wtime — «время терпения» и Success — «успеваемость во втором классе»). Сначала рассчитаем корреляцию между переменными.
Последовательно выберем пункты меню Regression – Correlation matrix. В открывшемся окне переносим переменные Wtime и Success в поле рабочих переменных справа. Получаем следующую таблицу.
| Correlation Matrix | |||||||
|---|---|---|---|---|---|---|---|
| Wtime | Success | ||||||
| Wtime | Pearson’s r | — | |||||
| p-value | — | ||||||
| Success | Pearson’s r | 0.500 | — | ||||
| p-value | 0.667 | — | |||||
Собственно корреляция между нашими переменными имеет величину 0.5, а соответствующая значимость равна 0.667.
Теперь проведем линейную регрессию. Выберем в меню пункты Regression — Linear Regression. В открывшемся окне перенесем переменную Success в окно зависимой переменной (Dependent Variable), а переменную Wtime в окно для независимой переменной, выраженной в численной шкале (Covariates). В разделе Model coefficients выберем ANOVA test и Standardized estimate. (Обратите внимание, что в этом же разделе можно выбрать расчет доверительного интервала для сырых коэффициентов и стандартизованного коэффициента β). Получаем таблицы:
| Model Fit Measures | |||||
|---|---|---|---|---|---|
| Model | R | R² | |||
| 1 | 0.500 | 0.250 | |||
| Omnibus ANOVA Test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sum of Squares | df | Mean Square | F | p | |||||||
| Wtime | 0.500 | 1 | 0.500 | 0.333 | 0.667 | ||||||
| Residuals | 1.500 | 1 | 1.500 | ||||||||
| Note. Type 3 sum of squares | |||||||||||
| Model Coefficients — Success | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | Stand. Estimate | ||||||
| Intercept | 4.000 | 0.707 | 5.657 | 0.111 | |||||||
| Wtime | 0.500 | 0.866 | 0.577 | 0.667 | 0.500 | ||||||
В первой таблице нам представлены коэффициент корреляции R и показатель качества модели R2.
Во второй — рассчитанные нами выше суммы квадратов: регрессия (regression), остаток (residuals). Это те самые 0.5 и 1.5, которые мы получили в расчетах предыдущего пункта. Далее с этими числами производятся операции, аналогичные тем, которые производились в дисперсионном анализе: суммы квадратов делятся на число степеней свободы (здесь они обе равны единице, в других примерах это будут другие числа), и затем 0.5 (регрессия) делится на 1.5 (остаток). Получается F-отношение 0.333, которому соответствует значимость 0.667 — та же самая, что и значимость корреляции, которую мы посчитали выше. Для простой линейной регрессии это всегда так.
В третьей таблице приведены регрессионные коэффициенты. В столбце, озаглавленном «Estimate», первое число — это свободный член (в нашем случае, когда переменная Wtime центрирована, свободный член равен среднему по трем наблюдениям переменной Success), а второе число — угловой коэффициент регрессионного уравнения: 0.5.
В столбце, озаглавленном «Stand. estimate», даны регрессионные коэффициенты, как если бы уравнение составлялось после стандартизации переменных. Свободный член в этом случае равен всегда нулю и поэтому не приводится. Угловой коэффициент в нашем примере тот же самый, потому что дисперсии наших переменных равны единице и стандартизация бы их не изменила. В следующем примере мы получим различие стандартизованных и нестандартизованных коэффициентов. Далее, можно оценить значимость результата (т.е. рассчитанного регрессионного коэффициента) относительно нулевой гипотезы (регрессионный коэффициент равен нулю — т.е. успешность в школе не зависит линейно от времени ожидания) [3][\simple_tooltip]. Для этого, деля нестандартизованный коэффициенты регрессии на его стандартную ошибку (0.500/0.866=0.577), получим показатель, сравнив который с t-распределением Стьюдента узнаем, какой хвост отсекают эти значения, или их значимость. В случае одной независимой переменной эти результаты совпадают с результатами дисперсионного анализа: F-отношение и t углового коэффициента связаны формулой \( F=t^2 \), а значимости одинаковы [4].
Чтобы графически представить полученный результат, в дополнительных модулях на командной панели справа (Modules), нужно нажать на «+» и выбрать блок scatr. Теперь в разделе Exploration появится раздел Scatterplot, выбрав который можно перенести Wtime в X—axis (то есть расположить эту переменную по оси абсцисс), а Success в Y—axis (по оси ординат). Чтобы увидеть на графике линию регрессии, Regression line отметьте пункт Linear.
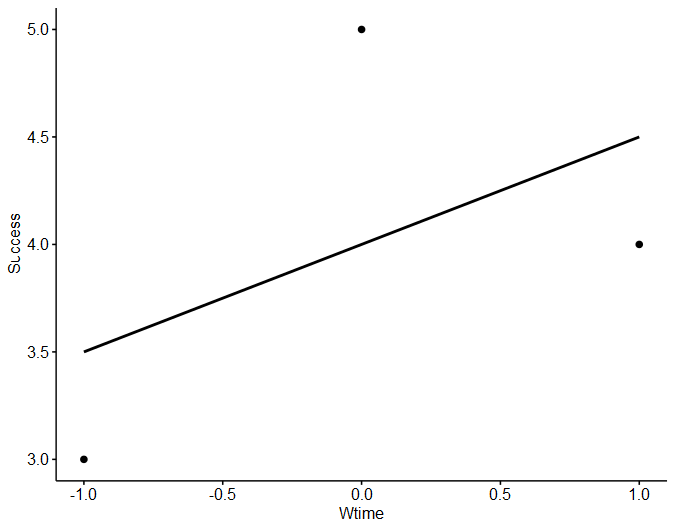
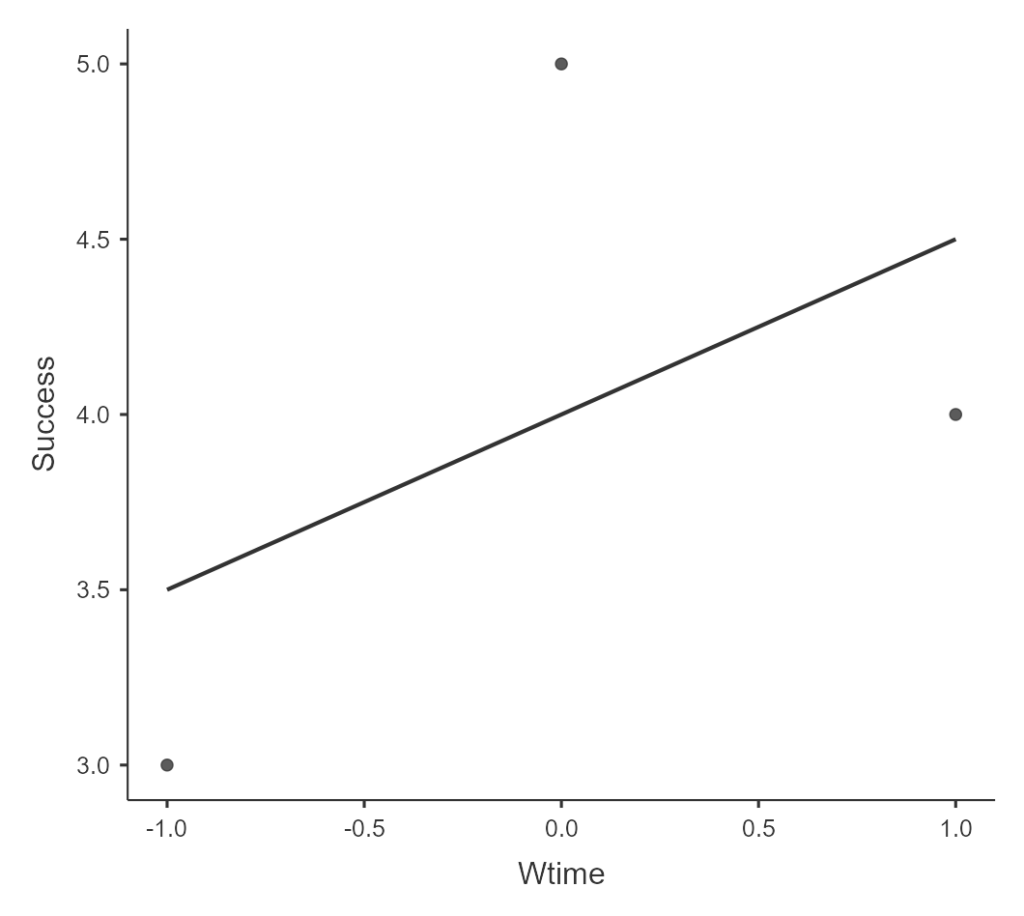Рис. 9.3(4)j. График рассеяния с линией регрессии для модели из трех точек
Заметим в заключение, что показатель R2 может быть получен как возведением в квадрат коэффициента корреляции, так и делением суммы регрессии (0.5) на общую сумму (2). Второй способ прямо связан с оценками моделей в других, более сложных случаях.
Теперь рассмотрим, как можно решить такую задачу с помощью R. Откроем файл Wtime.sav, загрузив его в таблицу w_time. Он содержит наши три наблюдения (переменные Wtime — «время терпения» и Success — «успеваемость во втором классе»):
library(foreign)
w_time <- read.spss("Wtime.sav", to.data.frame = T, reencode = "utf8")
w_time
Wtime Success
1 -1 3
2 0 5
3 1 4
Сначала рассчитаем корреляцию между переменными. Коэффициент корреляции Пирсона в R можно рассчитать с помощью функции cor, указав в качестве аргументов две коррелируемые переменные:
cor(w_time$Wtime, w_time$Success) [1] 0.5
Эта функция не оценивает значимость полученного результата, для поучения более полного результата, включающего оценку значимости результата можно использовать функцию corr.testиз пакета psych. В случае расчёта корреляции между двумя переменными эта функция выводит по умолчанию значение коэффициента корреляции, размер выборки и значимость коэффициента[5]:
library(psych) corr.test(w_time$Wtime, w_time$Success) Call:corr.test(x = w_time$Wtime, y = w_time$Success) Correlation matrix [1] 0.5 Sample Size [1] 3 These are the unadjusted probability values. The probability values adjusted for multiple tests are in the p.adj object. [1] 0.67 To see confidence intervals of the correlations, print with the short=FALSE option
Видно, что корреляция между нашими переменными имеет величину 0.5, а соответствующая значимость равна 0.667.
Теперь проведем линейную регрессию. Это можно сделать с помощью функции lm(от linear model). Минимально необходимо указать формулу соотношения зависимой и независимой переменной и название таблицы данных. Напоминим, что формула имеет вид Зависимая_переменная ~ Независимая(-ые)_переменная(-ые). В нашем примере это, соответственно Success ~ Wtime. Результат регрессии в R удобно сохранять в отдельную переменную и потом к ней обращаться для подробного рассмотрения полученных коэффициентов и оценок модели. Сохраним результат в переменную w_time_model:
w_time_model <- lm(Success ~ Wtime, data=w_time)
Основной результат линейной регрессии можно получив, запросив summary сохраненённой модели:
summary(w_time_model) Call: lm(formula = Success ~ Wtime, data = w_time) Residuals: 1 2 3 -0.5 1.0 -0.5 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 4.0000 0.7071 5.657 0.111 Wtime 0.5000 0.8660 0.577 0.667 Residual standard error: 1.225 on 1 degrees of freedom Multiple R-squared: 0.25, Adjusted R-squared: -0.5 F-statistic: 0.3333 on 1 and 1 DF, p-value: 0.6667
В начале приводится формула регрессии, затем остатки (ошибки) модели для каждой из точек (в этом примере их всего три).
Затем приведены регрессионные коэффициенты. В столбце, озаглавленном «Estimate», первое число — это свободный член (в нашем случае, когда переменная Wtime центрирована, свободный член равен 4 – среднему по трем наблюдениям переменной Success), а второе число — угловой коэффициент регрессионного уравнения: 0.5. Далее, можно оценить значимость результата (т.е. рассчитанного регрессионного коэффициента) относительно нулевой гипотезы (регрессионный коэффициент равен нулю — т.е. успешность в школе не зависит линейно от времени ожидания) [3][\simple_tooltip]. Для этого, деля нестандартизованный коэффициенты регрессии на его стандартную ошибку (0.500/0.866=0.577), получим показатель, сравнив который с t-распределением Стьюдента узнаем, какой хвост отсекают эти значения, или их значимость. В случае одной независимой переменной эти результаты совпадают с результатами дисперсионного анализа, описанного ниже: F-отношение и t углового коэффициента связаны формулой F=t2, а значимости одинаковы [4].
Затем указаны стандартные ошибка остатков (она может быть полезна для оценки качества модели). Следующая строка – содержит значения показателей качества модели — коэффициент множественный R2 и cкорректированный R2 (который важен в случае множественной регрессии, остановимся на этом позже).
Наконец, последняя строка содержит оценку соотношения сумм квадратов, рассчитанных нами выше. Остановимся на ней подробнее, для её детального рассмотрения можно рассчитать дисперсионный анализ модели, используя уже известную из прошлых глав функцию aovи вывести резюме:
summary(aov(w_time_model)) Df Sum Sq Mean Sq F value Pr(>F) Wtime 1 0.5 0.5 0.333 0.667 Residuals 1 1.5 1.5
Первая строка таблицы содержит степени свободы (столбец Df), сумму квадратов (столбец SumSq) и средний квадрат (столбец Mean Sq), соответствующие регрессионной модели, а вторая строка – те же показатели для остатков (Residuals). Суммы квадратов это те самые 0.5 и 1.5, которые мы получили в расчетах примера 9.3(1). Далее с этими числами производятся операции, аналогичные тем, которые производились в дисперсионном анализе: суммы квадратов делятся на число степеней свободы (здесь они обе равны единице, в других примерах это будут другие числа), и затем 0.5 (регрессия) делится на 1.5 (остаток). Получается F-отношение 0.333, которому соответствует значимость 0.667 — та же самая, что и значимость корреляции, которую мы посчитали выше. Для простой линейной регрессии это всегда так.
Также полезно, особенно в случае множественной регрессии, о которой речь пойдёт в следующей главе, рассмотреть стандартизованное решение модели. Это можно сделать, напрямую стандартизовав зависимую и независимые переменные с помощью функции scale:
w_time_model <- lm(scale(Success) ~ scale(Wtime), data=w_time) summary(w_time_model) Call: lm(formula = scale(Success) ~ scale(Wtime), data = w_time) Residuals: 1 2 3 -0.5 1.0 -0.5 attr(,"scaled:center") [1] 4 attr(,"scaled:scale") [1] 1 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.205e-17 7.071e-01 0.000 1.000 scale(Wtime) 5.000e-01 8.660e-01 0.577 0.667 Residual standard error: 1.225 on 1 degrees of freedom Multiple R-squared: 0.25, Adjusted R-squared: -0.5 F-statistic: 0.3333 on 1 and 1 DF, p-value: 0.6667
Статистика оценки модели не изменилась, а коэффициенты уравнения стали другими: свободный член в результате полной стандартизации переменных стал равен нулю (и это всегда так в случае стандартизованного решения). Угловой коэффициент в нашем примере остался тем же самым, потому что дисперсии наших переменных равны единице и стандартизация бы их не изменила. В следующем примере мы получим различие стандартизованных и нестандартизованных коэффициентов.
Чтобы графически представить полученный результат, можно нарисовать график рассеяния, наложив на него регрессионную прямую. Используя базовые графические функции R это можно делать следующим образом:
plot(w_time$Wtime, w_time$Success) abline(w_time_model, col="red")
Первая команда выводит график, на котором по оси Х отложена переменная Wtime , а по оси Y – Success. Вторая команда накладывает на график регрессионную прямую, соответствующую рассчитанной ранее модели, отображенную красным цветом (аргумент col). В результате будет полученный следующий график:
Рис. 9.3(4)r. График рассеяния с линией регрессии для модели из трех точек
Аналогичный график с возможностью настроек многочисленных дополнительных параметров можно получить, использовав функцию ggscatter, входящую в уже упомянутую в прошлой главе библиотекуggpubr. Самый простой вариант графика можно создать так:
library(ggpubr) ggscatter(data=w_time, x="Wtime", y="Success", add = "reg.line")
Рис. 9.3(5)r. График рассеяния с линией регрессии для модели из трех точек
Заметим в заключение, что показатель R2 , который мы видели выше, может быть получен как возведением в квадрат коэффициента корреляции, так и делением суммы регрессии (0.5) на общую сумму (2). Второй способ прямо связан с оценками моделей в других, более сложных случаях.
Упражнение 9.3(5). В файле WtimeM.sav (версия для SPSS, версия для Jamovi) добавлены еще две переменные, полученные из исходных преобразованиями \( Wtime2=Wtime*2+2,Success3=Success*3 \). Постройте две регрессионные модели, используя переменные Wtime и Wtime2 как независимые переменные и Success и Success3 — как зависимые в первом и втором анализе соответственно. Сравните две модели, убедитесь и объясните, почему:
— коэффициент корреляции не изменился;
— показатель качества модели R-квадрат не изменился;
— все суммы квадратов увеличились в \( 3*3 \) раз, а их отношение и соответствующая значимость не изменились;
— угловой коэффициент увеличился в 3/2 раза;
— изменился свободный член.
Пример 9.3(6). В файле simple.sav (версия для SPSS, версия для Jamovi) содержатся три ряда данных: \( x,y1, y2 \).
Упражнение 9.3(7). Постройте графики рассеяния следующих пар переменных: x и y1, x и y2. Добавьте на графики регрессионные прямые.
По форме рассеяния точек оцените, в каком из двух случаев при построении регрессионной прямой коэффициент детерминации будет выше. Проверьте свои предположения, произведя расчет регрессии.
Убедитесь, что регрессионные прямые, построенные на графиках рассеяния y1 по x и x по y1 не совпадают. Проведите регрессию x по y1. Для взаимно обратных линейных функций угловые коэффициенты подчиняются отношению \( a1*a2=1 \). Проверьте, что это соотношение в нашем случае не выполняется. Проверьте также, что показатели R и R2 совпадают.
В файле conflict.sav содержатся модельные данные исследования, задачей которого было выявить индикаторы крепости супружеских отношений. Молодых супругов приглашали для исследования в помещение, где просили подождать начала эксперимента. Для того чтобы скоротать время ожидания, испытуемым предлагали посмотреть журналы мод с фотографиями моделей. Оценивалось количество времени, которое испытуемый смотрел на фотографии лиц противоположного пола (переменная lookingtime содержит время, измеренное в минутах). Через два года при помощи интервью по нескольким параметрам оценивали выраженность конфликтов в супружеской паре (переменная conflictness). В таблицу данных занесены также показатели времени для нескольких новых участников эксперимента, у которых данных о конфликтности еще нет.
Проведите регрессионный анализ. После заполнения именами переменных полей зависимых и независимых переменных нажмите кнопку Сохранить и поставьте галочку в клетку Предсказанные значения — Нестандартизованные. В результате выполнения регрессионного анализа в таблице данных появится еще один столбец, содержащий предсказанные значения, в том числе и для новых участников. Проверьте, что эти значения для всех получаются из регрессионного уравнения, коэффициенты которого даны в соответствующей таблице вывода в столбце B. Обратите внимание, что регрессия «объясняет» не очень большую долю дисперсии переменной conflictness (R2 равен 0.288), и хотя значимость регрессионного коэффициента (и коэффициента корреляции R) достаточно близка к нулю (0.001), все же интерпретировать результат надо с осторожностью. Мы продолжим обсуждение этих данным ниже.
(Скрипт соответствующий этому примеру можно скачать по ссылке)
В файле conflict.sav содержатся модельные данные исследования, задачей которого было выявить индикаторы крепости супружеских отношений. Молодых супругов приглашали для исследования в помещение, где просили подождать начала эксперимента. Для того чтобы скоротать время ожидания, испытуемым предлагали посмотреть журналы мод с фотографиями моделей. Оценивалось количество времени, которое испытуемый смотрел на фотографии лиц противоположного пола (переменная lookingtime содержит время, измеренное в минутах). Через два года при помощи интервью по нескольким параметрам оценивали выраженность конфликтов в супружеской паре (переменная conflictness). В таблицу данных занесены также показатели времени для нескольких новых участников эксперимента, у которых данных о конфликтности еще нет.
Проведите регрессионный анализ и сделайте выводы. Обратите внимание, что регрессия «объясняет» не очень большую долю дисперсии переменной conflictness (R2 равен 0.288), и хотя значимость регрессионного коэффициента (и коэффициента корреляции R) достаточно близка к нулю (0.001), все же интерпретировать результат надо с осторожностью.
Попробуем теперь узнать, какова предсказанная (на основе уже имеющихся данных) конфликтность тех семи человек, про которых известно только время просмотра лиц противоположного пола в журналах. Для этого перейдите в Data – Compute и в разделе f(x) введите = lookingtime*0.288+12.567.
Иными словами, если ввести формулу регрессионного уравнения (угловой коэффициент и свободный член), рассчитаются предсказанные (нестандартизованные) значения. У кого из этих семи человек вероятность конфликтов в браке самая высокая?
В файле conflict.sav содержатся модельные данные исследования, задачей которого было выявить индикаторы крепости супружеских отношений. Молодых супругов приглашали для исследования в помещение, где просили подождать начала эксперимента. Для того чтобы скоротать время ожидания, испытуемым предлагали посмотреть журналы мод с фотографиями моделей. Оценивалось количество времени, которое испытуемый смотрел на фотографии лиц противоположного пола (переменная lookingtime содержит время, измеренное в минутах). Через два года при помощи интервью по нескольким параметрам оценивали выраженность конфликтов в супружеской паре (переменная conflictness). В таблицу данных занесены также показатели времени для нескольких новых участников эксперимента, у которых данных о конфликтности еще нет.
Задайте регрессионную модель с помощью функции lm, сохраните её в переменную conflict_regr, выведите результаты регрессионного анализа, используя функцию summary. Проанализировав таблицу коэффициентов, выпишите уравнение регрессии для заданной модели. Затем рассчитайте предсказываемые моделью значения зависимой переменной, используя функцию predict, первый аргумент которой – заданная модель conflict_regr, а второй – newdata – должен указывать на полную таблицу данных включающую новых испытуемых (если таблица данных называется data_conflict, то newdata = conflict_data). Сохраните предсказанные значения в новую переменную conflictness_predicted исходной таблицы данных:
data_conflict$conflictness_predicted <- predict(conflict_regr, newdata = data_conflict)
В результате в таблице данных появится еще один столбец, содержащий предсказанные значения, в том числе и для новых участников. Проверьте, что эти значения для всех получаются из регрессионного уравнения, коэффициенты которого даны в соответствующей таблице вывода в столбце B. Их можно рассчитать напрямую:
data_conflict$conflictness_predicted_handmade <- 0.288 * data_conflictness$lookingtime + 12.567
Долю объясняемой моделью дисперсии можно рассчитать, вычтя из единицы отношение дисперсии остатков (разности между реальными и модельными значениями конфликтности) к дисперсии реальной конфликтности:
1-(var(data_conflict$conflictness - data_conflict$conflictness_predicted, na.rm = T)/var(data_conflict$conflictness, na.rm = T))
Обратите внимание, что предсказанные значения не совпадают с реальными значениями конфликтности, так как регрессия «объясняет» не очень большую долю дисперсии переменной conflictness (R2 равен 0.288), и, хотя значимость регрессионного коэффициента (и коэффициента корреляции R) достаточно близка к нулю (0.001), все же интерпретировать результат надо с осторожностью. Мы продолжим обсуждение этих данным ниже.
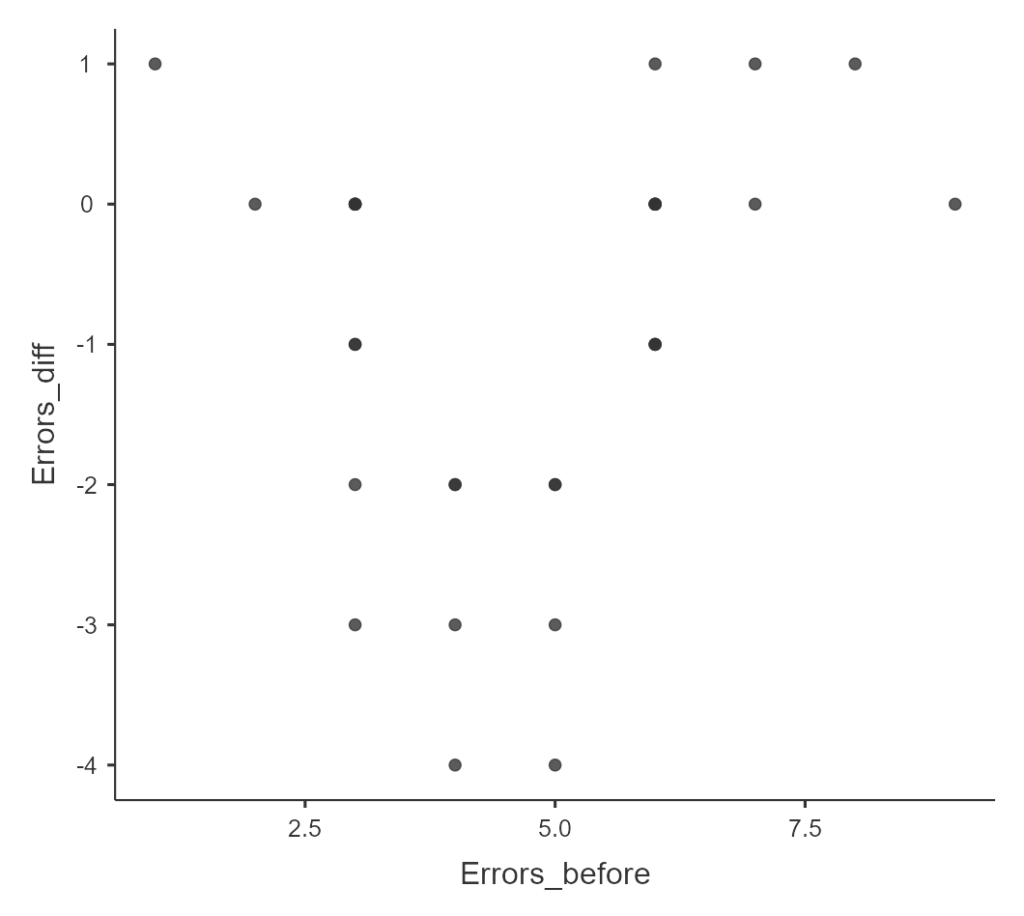
Пример 9.3(9). Нелинейные связи в простой линейной регрессии в SPSS. Предположим, классный руководитель решил проводить дополнительные занятия по русскому языку с учениками, которые сделали ошибки в сложном диктанте, а затем оценивал, насколько меньше ошибок ученики сделали после проведенных занятий. Учителя интересовало, кому из учеников эти занятия наиболее полезны — «хорошистам», делающим мало ошибок, «середнячкам» со средним количеством ошибок или неуспевающим детям, делающим много ошибок. В файле ErrorsTraining.sav смоделированы результаты такого исследования для 30 школьников: количество ошибок в первом диктанте зафиксировано в переменной ErrorsBefore. Изменение к следующему диктанту описывается переменной ErrorsDiff (отрицательные числа означают, что ошибок стало меньше, положительные — что больше).
Описательные статистики показывают, что среднее число ошибок после первого диктанта — чуть меньше пяти, а занятия в среднем уменьшают это значение почти на одну ошибку. Результаты регрессионного анализа показывают, что от количества ошибок в начале прогресс школьников не зависит (процент объясняемой дисперсии \( R^2=0.044 \), оценка значимости \( F=1.296,p=0.265 \)).
| Описательные статистики | |||||
| N | Минимум | Максимум | Среднее | Среднекв. отклонение | |
| ErrorsBefore | 30 | 1.00 | 9.00 | 4.7333 | 1.85571 |
| ErrorsDiff | 30 | -4.00 | 1.00 | -0.9333 | 1.46059 |
| N валидных (по списку) | 30 | ||||
| Сводка для модели | ||||
| Модель | R | R-квадрат | Скорректированный R-квадрат | Стандартная ошибка оценки |
| 1 | 0.210a | 0.044 | 0.010 | 1.45319 |
| a. Предикторы: (константа), Errors_before | ||||
| ANOVAa | ||||||
| Модель | Сумма квадратов | ст.св. | Средний квадрат | F | Значимость | |
| 1 | Регрессия | 2.737 | 1 | 2.737 | 1.296 | 0.265b |
| Остаток | 59.130 | 28 | 2.112 | |||
| Всего | 61.867 | 29 | ||||
| a. Зависимая переменная: ErrorsDiff | ||||||
| b. Предикторы: (константа), ErrorsBefore | ||||||
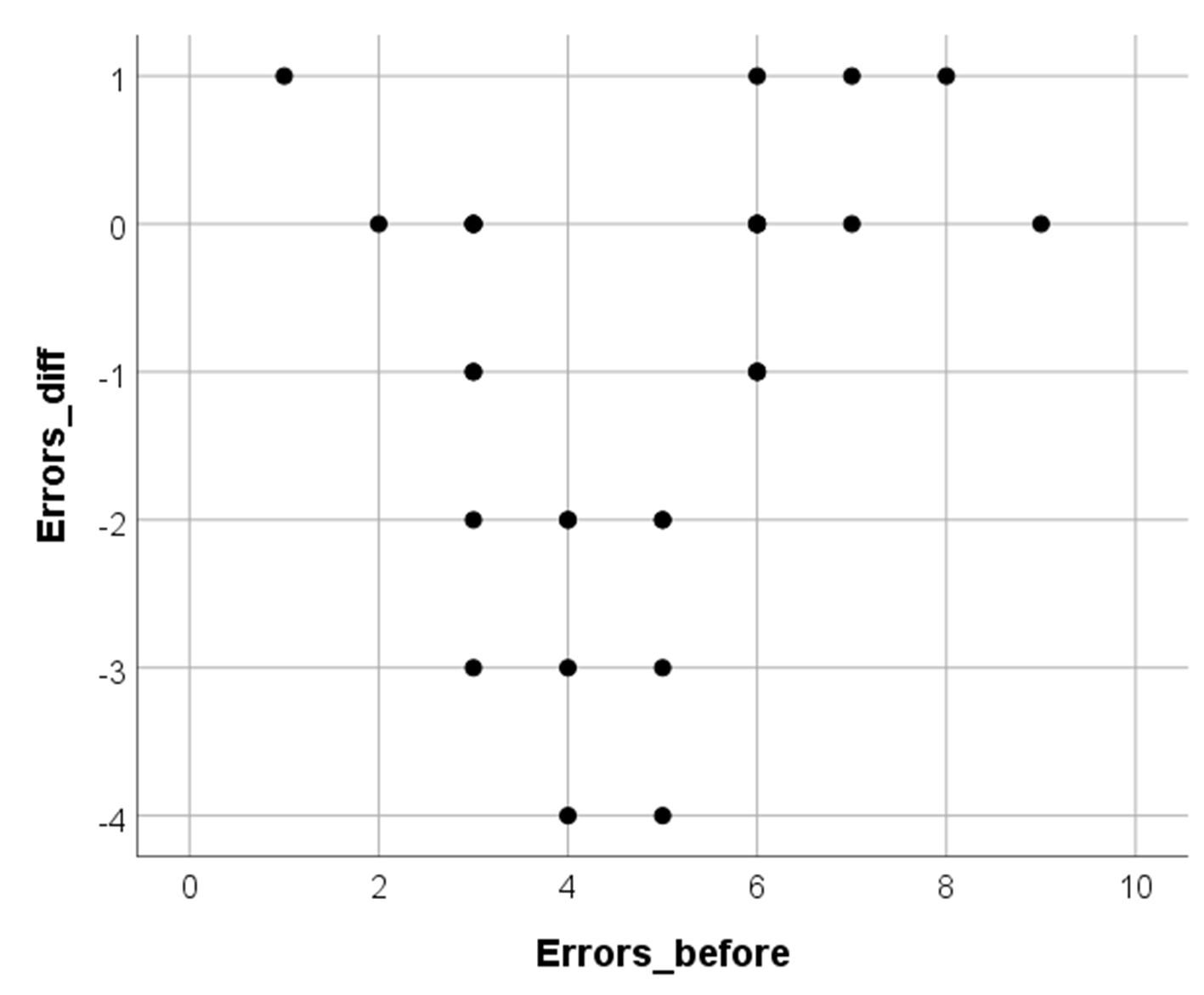
Однако по диаграмме рассеяния, изображенной на рис. 9.3(10), кажется, что закономерность все же есть: похоже, занятия хорошо работают в случае «середнячков» и малоэффективны у «хорошистов» и неуспевающих.
Рис. 9.3(10). График рассеяния исходного числа ошибок в диктанте и изменения числа ошибок во втором диктанте
Такого рода гипотезы — о нелинейных закономерностях — требуют применения нелинейной регрессии (в нашем учебнике мы не будем обсуждать эти методы). Тем не менее, оставаясь в рамках линейной регрессии, можно предварительно сориентироваться в ситуации. Разделим выборку на две части в соответствии со средним значением: тем, кто сделал 4 и менее ошибки, припишем «1», тем, что 5 и более, припишем «2» (переменная Group) и проведем регрессионный анализ отдельно в двух группах. Для этого выберем Данные — Расщепить файл (Data — Split file), укажем Сравнить группы (Compare groups) и перенесем в поле справа (Группы образуются по, (Groups based on)) переменную Group. Весь дальнейший анализ будет проводиться отдельно в выделенных группах до тех пор, пока мы не уберем эту установку (выбрав Анализировать все наблюдения, группы не создавать, (Analyze all cases, do not create groups)).
Повторив теперь процедуру задания регрессионного анализа для переменной ErrorsDiff, получим две серии таблиц. Обе линейные модели для двух подвыборок теперь характеризуются близкими к нулю значимостями и имеют достаточно высокие показатели R2: модель для хорошо успевающих учеников объясняет 54.9% дисперсии изменений в количестве ошибок, а у слабых учеников — 44.5%. Как видно в таблице коэффициентов, если рассматривать успевающих учеников, занятия лучше помогают тем, кто делает больше ошибок; если слабых — наоборот.
| Коэффициентыa | |||||||
| Group | Модель | Нестандартизованные коэффициенты | Стандартизованные коэффициенты | т | Значимость | ||
| B | Стандартная ошибка | Бета | |||||
| 1 | 1 | (Константа) | 2.840 | 1.097 | 2.589 | 0.024 | |
| ErrorsBefore | -1.320 | .346 | -0.741 | -3.819 | 0.002 | ||
| 2 | 1 | (Константа) | -6.078 | 1.633 | -3.723 | 0.002 | |
| ErrorsBefore | 0.871 | 0.260 | 0.667 | 3.351 | 0.005 | ||
| a. Зависимая переменная: Errors_diff | |||||||
Упражнение 9.3(11). Постройте две диаграммы рассеяния для успевающих и слабых учеников и рассчитайте для них регрессионную модель. Проинтерпретируйте результат.
Пример 9.3(9)j. Нелинейные связи в простой линейной регрессии Jamovi. Предположим, классный руководитель решил проводить дополнительные занятия по русскому языку с учениками, которые сделали ошибки в сложном диктанте, а затем оценивал, насколько меньше ошибок ученики сделали после проведенных занятий. Учителя интересовало, кому из учеников эти занятия наиболее полезны — «хорошистам», делающим мало ошибок, «середнячкам» со средним количеством ошибок или неуспевающим детям, делающим много ошибок. В файле ErrorsTraining.sav смоделированы результаты такого исследования для 30 школьников: количество ошибок в первом диктанте зафиксировано в переменной ErrorsBefore. Изменение к следующему диктанту описывается переменной ErrorsDiff (отрицательные числа означают, что ошибок стало меньше, положительные — что больше).
Описательные статистики показывают, что среднее число ошибок после первого диктанта — чуть меньше пяти, а занятия в среднем уменьшают это значение почти на одну ошибку. Результаты регрессионного анализа показывают, что от количества ошибок в начале прогресс школьников не зависит (процент объясняемой дисперсии \( R^2=0.0442 \), оценка значимости \( F(1, 28=1.296,p=0.265 \)).
| Descriptives | |||||
|---|---|---|---|---|---|
| Errors_before | Errors_diff | ||||
| Mean | 4.733 | -0.933 | |||
| Median | 5.000 | -0.500 | |||
| Standard deviation | 1.856 | 1.461 | |||
| Minimum | 1 | -4.000 | |||
| Maximum | 9 | 1.000 | |||
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.210 | 0.044 | 1.296 | 1 | 28 | 0.265 | |||||||
| Model Coefficients — Errors_diff | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | |||||
| Intercept | -1.717 | 0.738 | -2.328 | 0.027 | |||||
| Errors_before | 0.166 | 0.145 | 1.138 | 0.265 | |||||
Однако по диаграмме рассеяния (напоминаем, что для этого нужно добавить Module — scatr и внести переменные на Scatterplot), изображенной на рис. 9.3(10)j, кажется, что закономерность все же есть: похоже, занятия хорошо работают в случае «середнячков» и малоэффективны у «хорошистов» и неуспевающих.
Рис. 9.3(10)j. График рассеяния исходного числа ошибок в диктанте и изменения числа ошибок во втором диктанте
Такого рода гипотезы — о нелинейных закономерностях — требуют применения нелинейной регрессии (в нашем учебнике мы не будем обсуждать эти методы). Тем не менее, оставаясь в рамках линейной регрессии, можно предварительно сориентироваться в ситуации. Разделим выборку на две части в соответствии со средним значением: тем, кто сделал 4 и менее ошибки, припишем «1», тем, что 5 и более, припишем «2» (переменная Group) и проведем регрессионный анализ отдельно в двух группах.
В Jamovi для этого придется использовать функцию Filters в закладке Data. Введите в Filters “Group==1” и должен получиться следующий результат.
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.741 | 0.549 | 14.585 | 1 | 12 | 0.002 | |||||||
| Model Coefficients — Errors_diff | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | |||||
| Intercept | 2.840 | 1.097 | 2.589 | 0.024 | |||||
| Errors_before | -1.320 | 0.346 | -3.819 | 0.002 | |||||
Теперь введите в Filters “Group==2” и результат будет иным.
| Model Fit Measures | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Overall Model Test | |||||||||||||
| Model | R | R² | F | df1 | df2 | p | |||||||
| 1 | 0.667 | 0.445 | 11.231 | 1 | 14 | 0.005 | |||||||
| Model Coefficients — Errors_diff | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Predictor | Estimate | SE | t | p | |||||
| Intercept | -6.078 | 1.633 | -3.723 | 0.002 | |||||
| Errors_before | 0.871 | 0.260 | 3.351 | 0.005 | |||||
Обе линейные модели для двух подвыборок теперь характеризуются близкими к нулю значимостями и имеют достаточно высокие показатели R2: модель для хорошо успевающих учеников объясняет 54.9% дисперсии изменений в количестве ошибок, а у слабых учеников — 44.5%. Как видно в таблице коэффициентов, если рассматривать успевающих учеников, занятия лучше помогают тем, кто делает больше ошибок; если слабых — наоборот.
Упражнение 9.3(11). Используя ту же функцию Filters, постройте две диаграммы рассеяния для успевающих и слабых учеников и рассчитайте для них регрессионную модель. Проинтерпретируйте результат.
Предположим, классный руководитель решил проводить дополнительные занятия по русскому языку с учениками, которые сделали ошибки в сложном диктанте, а затем оценивал, насколько меньше ошибок ученики сделали после проведенных занятий. Учителя интересовало, кому из учеников эти занятия наиболее полезны — «хорошистам», делающим мало ошибок, «середнячкам» со средним количеством ошибок или неуспевающим детям, делающим много ошибок. В файле ErrorsTraining.sav смоделированы результаты такого исследования для 30 школьников: количество ошибок в первом диктанте зафиксировано в переменной ErrorsBefore. Изменение к следующему диктанту описывается переменной ErrorsDiff (отрицательные числа означают, что ошибок стало меньше, положительные — что больше).
Если рассчитать описательные статистики, они покажут, что среднее число ошибок после первого диктанта — чуть меньше пяти, а занятия в среднем уменьшают это значение почти на одну ошибку:
library(foreign)
library(psych)
data_errors<- read.spss("ErrorsTraining.sav", to.data.frame = T, reencode = "utf8")
describe(data_errors[, 1:2])
vars n mean sd median trimmed mad min max range skew kurtosis se
Errors_before 1 30 4.73 1.86 5.0 4.67 1.48 1 9 8 0.19 -0.63 0.34
Errors_diff 2 30 -0.93 1.46 -0.5 -0.83 0.74 -4 1 5 -0.56 -0.79 0.27
Результаты регрессионного анализа показывают, что от количества ошибок в начале прогресс школьников не зависит (процент объясняемой дисперсии R2=0.044, оценка значимости F=1.296, p=0.265).
summary(lm(Errors_diff ~ Errors_before, data = data_errors)) Call: lm(formula = Errors_diff ~ Errors_before, data = data_errors) Residuals: Min 1Q Median 3Q Max -3.1108 -0.9453 0.2236 1.2203 2.5514 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -1.7170 0.7377 -2.328 0.0274 * Errors_before 0.1656 0.1454 1.138 0.2646 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.453 on 28 degrees of freedom Multiple R-squared: 0.04424, Adjusted R-squared: 0.01011 F-statistic: 1.296 on 1 and 28 DF, p-value: 0.2646
Однако по диаграмме рассеяния, изображенной на рис. 9.3(10)r, кажется, что закономерность все же есть: похоже, занятия хорошо работают в случае «середнячков» и малоэффективны у «хорошистов» и неуспевающих.
plot(data_errors$Errors_before, data_errors$Errors_diff, pch=16)
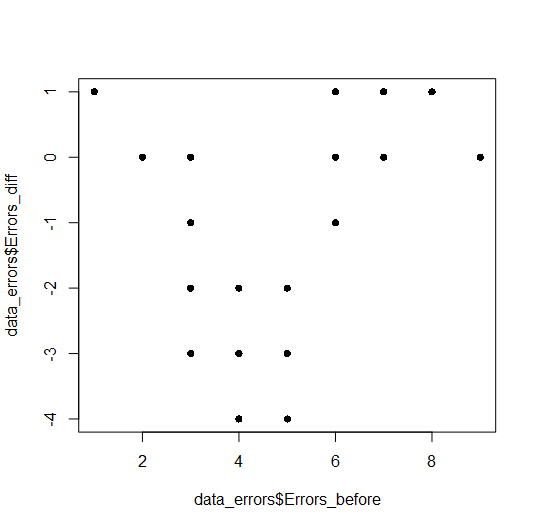Рис. 9.3(10)r. График рассеяния исходного числа ошибок в диктанте и изменения числа ошибок во втором диктанте
Такого рода гипотезы — о нелинейных закономерностях — требуют применения нелинейной регрессии (в нашем учебнике мы не будем обсуждать эти методы). Тем не менее, оставаясь в рамках линейной регрессии, можно предварительно сориентироваться в ситуации. Разделим выборку на две части в соответствии со средним значением: тем, кто сделал 4 и менее ошибки, припишем «1», тем, что 5 и более, припишем «2» (переменная Group) и проведем регрессионный анализ отдельно в двух группах.
В R это можно сделать с помощью функции split, первым аргументом которой надо указать массив разбиваемых данных, а вторым – переменную разбиения. В результате будет получен список, состоящий из наборов данных, соответствующих каждому из уровней переменной разбиения:
split_data_errors <- split(data_errors, f=data_errors$Group)
Чтобы провести анализ отдельно для каждой из полученных подвыборок, можно использовать функции семейства apply(в зависимости от задачи это могут быть lapply, sapply, tapply) или же напрямую обращаться к отдельным элементам списка, указывая их номера в двойных квадратных скобках. Воспользуемся вторым вариантом и повторим регрессионный анализ дважды, для первой и второй подгруппы:
summary(lm(Errors_diff ~ Errors_before, data = split_data_errors[[1]])) Call: lm(formula = Errors_diff ~ Errors_before, data = split_data_errors[[1]]) Residuals: Min 1Q Median 3Q Max -1.88 -0.55 0.12 0.95 1.12 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.8400 1.0969 2.589 0.02370 * Errors_before -1.3200 0.3456 -3.819 0.00244 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.033 on 12 degrees of freedom Multiple R-squared: 0.5486, Adjusted R-squared: 0.511 F-statistic: 14.58 on 1 and 12 DF, p-value: 0.002444 summary(lm(Errors_diff ~ Errors_before, data = split_data_errors[[2]])) Call: lm(formula = Errors_diff ~ Errors_before, data = split_data_errors[[2]]) Residuals: Min 1Q Median 3Q Max -2.27797 -0.27797 -0.08475 0.85085 1.85085 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -6.0780 1.6325 -3.723 0.00227 ** Errors_before 0.8712 0.2600 3.351 0.00475 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.116 on 14 degrees of freedom Multiple R-squared: 0.4451, Adjusted R-squared: 0.4055 F-statistic: 11.23 on 1 and 14 DF, p-value: 0.004752
Обе линейные модели для двух подвыборок теперь характеризуются близкими к нулю значимостями и имеют достаточно высокие показатели R2: модель для хорошо успевающих учеников объясняет 54.9% дисперсии изменений в количестве ошибок, а у слабых учеников — 44.5%. Как видно в таблице коэффициентов, если рассматривать успевающих учеников, занятия лучше помогают тем, кто делает больше ошибок; если слабых — наоборот.
Упражнение 9.3(11)r. Постройте две диаграммы рассеяния для успевающих и слабых учеников и рассчитайте для них регрессионную модель.
Сделать в R это можно либо нарисовав два графика с помощью базовой функции plotотдельно для каждого из элемента списка:
plot(split_data_errors[[1]]$Errors_before, split_data_errors[[1]]$Errors_diff, pch=16) plot(split_data_errors[[2]]$Errors_before, split_data_errors[[2]]$Errors_diff, pch=16)
Другой вариант — использовать систему ggplot, добавив функцию facet_wrap, разбивающую исходный массив данных на две части по указанной переменной. Также, используя функцию geom_smoothсо значением аргумента method = "lm" можно отобразить на графиках регрессионные прямые:
ggplot(data_errors, aes(x = Errors_before, y = Errors_diff)) + geom_point() + geom_smooth(method="lm") + facet_wrap(~Group)
Проинтерпретируйте результат.
Итак, как и в случае корреляции, незначимость регрессионной модели не означает отсутствия связи, и диаграммы рассеяния и описательная статистика — незаменимые помощники на предварительном этапе анализа данных.
Пример 9.3(12). В примере 9.3(8) саму связь между независимой и зависимой переменными было точнее описывать как нелинейную. Рассмотрим еще более сложную зависимость: случай, когда связь зависит от какой-то другой, внешней по отношению к исследованию переменной. В файле conflictCB.sav (версия для SPSS, версия для Jamovi) мы модифицировали данные обсуждавшегося выше исследования связи времени рассматривания фотографий лиц противоположного пола и конфликтов в браке через два года. Предположим, что в исследовании участвовали только женщины, недавно вступившие в брак, и за два года некоторые из них успели родить ребенка. Эта информация отражена в переменной ChildBirth, где «0» — нет ребенка, «1» — есть.
Упражнение 9.3(13). Проведите линейную регрессию отдельно в этих двух группах и сравните результаты.
(В SPSS используйте опцию Расщепить файл, а в Jamovi для этого Вам будет нужно вновь воспользоваться функцией Filters и введя f(x)=child_birth==1 и f(x)=child_birth==0, соответственно, провести простую линейную регрессию).
Обратите внимание, что ни по длительности рассматривания фотографий, ни по конфликтности в среднем обе группы женщин не различаются. Это можно проверить при помощи t-критерия Стьюдента: средняя длительность составляет 16.02 у женщин без детей и 15.81 у родивших (\( t=0.151,p=0.881 \)), а средняя конфликтность составляет 17.06 и 17.25 соответственно (\( t=-0.262,p=0.595 \)).
Сравнение двух простых линейных регрессий показывает, что найденная в целом по выборке связь (описанная в примере 9.3(12)) есть и даже значительно более выражена только у бездетных женщин (R2 = 54.4%, по сравнению с 28.8% в общей выборке). У тех, кто родил ребенка, уровень конфликтности в семье такой же, но он не связан с просмотром фотографий два года назад.
Такая ситуация носит название модерации: эффект длительности просмотра фотографий на конфликтность в браке зависит от того, как развивался этот брак. Переменная ChildBirth выступает переменной-модератором связи независимой и зависимой переменными. Из-за модерации закономерности, полученные в общей выборке, могут быть слабее, чем в одной из групп (как в нашем случае), не выявляться или даже быть столь же бессмысленными, как и «средняя температура по больнице». В главе 10 анализ модерации и процедура его проведения описаны подробнее.
>> следующий параграф>>
[1] Вместо \( S_{model} \) мы будем писать теперь \( S_{regression} \), а вместо \( S_{error} \) — \( S_{residual} \), чтобы согласовываться с заголовками таблиц вывода SPSS
[2] Также в таблице приводится скорректированный R2, который важен при множественном регрессионном анализе, подробнее о нем мы скажем в следующей главе
[3] Для свободного члена этот результат для нас неинтересен, это просто константа, связанная с разницей метрик независимой и зависимой переменной и почти всегда отличная от нуля, но он также рассчитывается по умолчанию.
[4] В главе 10 мы покажем, что когда независимых переменных несколько, F характеризует общее качество модели, а T-критерий направлен на проверку (не всегда удачную) того, насколько угловой коэффициент каждой из независимых переменных отличается от нуля.
[5] При расчете корреляции для нескольких переменных функций corr.test возвращает три соответствующие матрицы – корреляций, размера выборки (которая может меняться при наличии пропущенных значений – функции по умолчанию рассчитывает корреляцию между всем непропущенными значениями для каждой пар переменных), и матрицу значимостей. Матрица значимостей асимметрична: она содержит «сырую» оценку значимостей в верхней части и значимость с поправкой Хольма на множественное тестирование гипотез.