9.2.1. Корреляция и регрессия. Степени свободы. Сравнение с дисперсионным анализом. Мощность критерия
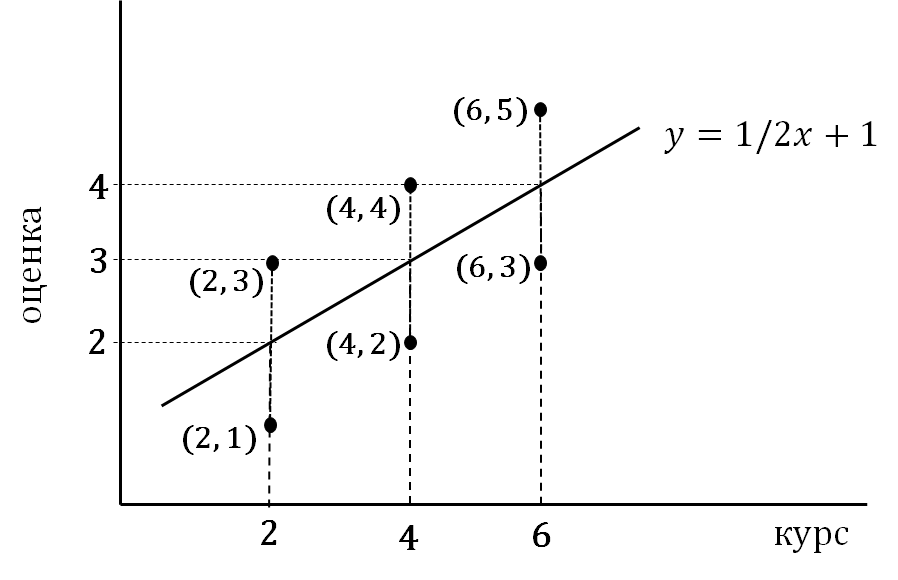
Мы сравним сейчас два метода — регрессионный и дисперсионный анализ — на простом примере из шести точек. Предположим, наши данные — это оценки знания математических методов у студентов соответствующего курса (номер курса задан абсциссой x). Уместность первого или второго метода определяется содержательной гипотезой, которую мы хотим оценить в нашем исследовании. Если мы (преподаватели математических методов) предполагаем, что наши лекции и семинары должны приводить и приводят к постоянному увеличению знаний студентов, то нашей гипотезе будет соответствовать рост средних значений. Пусть результат выражается парной выборкой (2, 1); (2, 3); (4, 2); (4, 4); (6, 3); (6, 5) (рис. 9.2.1(1)). Регрессионная прямая имеет угловой коэффициент 0.5 и проходит через точки (2, 2), (4, 3) и (6, 4) [1].
Рис. 9.2.1(1)). Регрессионная прямая для набора из 6 точек. Угловой коэффициент равен 0.5, прямая проходит через точки (2, 2), (4, 3) и (6, 4).
Сумма квадратов \( S_{model} \) задается ординатами проекций точек на регрессионную прямую (2, 2); (3, 3); (4, 4) относительно общего среднего, равного 3, и составляет \( S_{model}=(-1)^2+(-1)^2+0^2+0^2+1^2+1^2=4 \) (каждая пара точек, имеющих одну абсциссу, проецируется в одну точку прямой, которая поэтому учитывается дважды). Остаток \( S_{error}=6*1^2=6 \). Соответственно, \( S_{total}=S_{model}+S_{error}=4+6=10 \) Показатель качества модели \( R^2=S_{model}/S_{total}=0.4 \). Значимость нулевой гипотезы о равенстве нулю углового коэффициента регрессионной прямой определяется значением
\[ F^1_4=\frac{S_{model}/1}{S_{error}/4}=\frac{4}{1.5}=2.667. \]
Суммы квадратов в числителе и знаменателе мы делим на соответствующее число степеней свободы. Исходно их шесть — столько же, сколько точек. После вычитания \( \overline{y} \) их остается пять — поскольку \( \overline{y} \) вместе с любыми пятью числами определяют всю исходную шестерку чисел. Далее эти пять степеней свободы делятся на две части. Одна степень свободы (модели) приходится на управляемую одним лишь угловым коэффициентом прямую, проходящую через точку \( (\overline{x}, \overline{y}) \). Остальные четыре остаются остатку, или ошибке. Сумму квадратов в числителе мы делим на число степеней свободы модели, которое равно единице. На число четыре делится сумма остатка в знаменателе.
Мы привели здесь, скорее, мнемоническое правило, чем объяснение. Интересующихся более точными разъяснениями адресуем к приложению 4.
Вернемся к нашим данным. Проделаем теперь над этими же данными однофакторный дисперсионный анализ (три группы по два студента в каждой). Вычисляя, мы найдем те же самые суммы квадратов, что и в случае регрессии, поскольку групповые средние лежат на регрессионной прямой. Но F-отношение будет другим из-за иного соотношения степеней свободы:
\[ F^2_3=\frac{S_{model}/2}{S_{error}/3}=\frac{2}{2}=1. \]
Почему? После вычитания общего среднего \( \overline{y} \) модель дисперсионного анализа управляется двумя параметрами — среднее третьей группы дополняет сумму средних двух групп до нуля [2]. На остаток приходится теперь три степени свободы.
Подразумеваемое соображение, которое верно для случайных выборок, таково: для достаточно разумных моделей после вычитания общего среднего введение каждого нового параметра должно забирать из общей суммы квадратов примерно одинаковую порцию. Шесть параметров должны свести остаток к нулю, а всю сумму перевести в \( S_{model} \) (наилучшее приближение в этом случае сами числа). «Беда» модели дисперсионного анализа по сравнению с регрессионной в нашем случае в том, что, добавив параметр, позволяющий групповым средним не лежать на одной прямой, она не перевела ничего из суммы остатка в сумму модели. Это и означает, что для наших данных регрессионная модель лучше модели дисперсионного анализа, ее F-отношение больше, и значимость лучше.
Наши данные соответствуют гипотезе о монотонном и даже линейном росте уровня знаний у студентов. Если именно это мы и хотели доказать, то нам следовало заранее спланировать обработку результатов методом линейной регрессии. Если же неких нейтральных исследователей интересует всякая динамика знаний студентов и они заранее понимают, что и результат с максимальным уровнем знаний в середине времени обучения и забыванием материала к концу не менее интересен и также будет ими опубликован, то регрессионный анализ им недостаточен, поскольку процесс с обучением и забыванием не будет уловлен. В первом случае гипотеза более узкая и регрессионный метод ей адекватен. Во втором случае гипотеза шире, регрессионный метод для нее узок, а дисперсионный анализ адекватен. За эту адекватность в последнем случае мы платим тем, что, получив результат, как в разобранном примере, мы проигрываем в величине F-отношения и значимости.
Говорят, что по отношению к гипотезе о линейном росте знаний регрессионный метод более мощный, чем дисперсионный анализ [3].
«Мораль» нашего примера такова.
На языке статистической значимости: Совершенно честно и в то же время полезно для усиления наших результатов точно формулировать гипотезы исследования и подбирать соответствующий наиболее мощный критерий.
На языке моделей: Введение лишних параметров настройки модели может вообще не улучшить ситуацию с остатками, или может ее улучшить слабо, так что это улучшение не компенсирует рост числа степеней свободы модели (уменьшающий числитель F-отношения) и убывание числа степеней свободы остатка (увеличивающее знаменатель F-отношения). Выходя за пределы примера, можно сформулировать более общее утверждение. Введение бесполезных параметров (а также переменных, групп испытуемых и т.п.) в исследование может существенно ухудшить результат. Надежды на то, что сбор всевозможной информации без наличия разумных гипотез и направленного отбора позволит с помощью математической обработки получить хороший результат, при «честной игре» не оправдывается. Такой «неразборчивый» дизайн может работать только в пилотажном исследовании, результаты которого затем должны перепроверяться в исследовании с более точно сформулированными условиями и дизайном.
9.2.2. Ковариация и корреляция между случайными величинами
Пусть X и Y — дискретные случайные величины, распределение которых задано таблицами
| X | -1 | 1 | и | Y | -1 | 1 |
| p | 0.5 | 0.5 | p | 0.5 | 0.5 |
Если X и Y независимы, то вероятность одновременного наступления событий \( (X=-1, Y=-1) \) равна произведению вероятностей наступления каждого из событий в отдельности, т.е. 0.25 (аналогично для остальных пар событий \( (X=-1, Y=1 )\), \( (X=1, Y=-1) \) и \( (X=1, Y=1) \)). Однако так бывает далеко не всегда. Например, если \( X=1 \) кодирует событие «вес испытуемого выше среднего», а \( X=-1 \) — «вес ниже среднего», а случайная величина Y кодирует аналогичные высказывания про рост испытуемого, то понятно, что вероятность одновременного превышения среднего роста и среднего веса выше, чем вероятность наблюдать большой вес при маленьком росте. В этом случае имеет смысл говорить о совместном распределении случайных величин. Предположим, что для нашего примера оно может быть задано таблицей
| X = −1, Y = −1 | X = −1, Y = 1 | X = 1, Y = −1 | X = 1, Y = 1 |
| 0.4 | 0.1 | 0.1 | 0.4 |
Характеристикой степени отклонения этого распределения от распределения независимых величин служит корреляция.
Сначала вычислим теоретическую ковариацию \( COV_{xy} \). Для этого будем перемножать отклонения значений каждой из случайных величин от ее собственного математического ожидания и домножать произведение на вероятность совместного появления этих значений.
Первое слагаемое получается из первой клетки таблицы, где \( X=-1,Y=-1 \), а вероятность их совместного появления 0.4 берется из второй строки. В результате имеем произведение \( ((-1)-M_X)((-1)-M_Y)⋅p(X=-1,Y=-1) \) (хотя \( M_X=M_Y=0 \), мы оставляем их в формуле). Это слагаемое будет первым в формуле теоретической ковариации. Остальные слагаемые формируются аналогично.
\[ R_XY= \]
\[ =((-1)-M_X)((-1)-M_Y)⋅p(X=-1,Y=-1)+ \]
\[ +((-1)-M_X)((+1)-M_Y)⋅p(X=-1,Y=1)+ \]
\[ +((+1)-M_X)((-1)-M_Y)⋅p(X=1,Y=-1)+ \]
\[ +((+1)-M_X)((+1)-M_Y)⋅p(X=1,Y=1) \]
Подставляя значения вероятностей и учитывая, что \( M_X=M_Y=0 \), получаем \( R_{XY}=(-1)(-1)⋅0.4+(-1)(1)⋅0.1+(1)(-1)⋅0.1+(1)(1)⋅0.4=0.6. \)
Упражнение 9.2.2(1). Подставьте в предыдущую формулу вероятности 0.25, соответствующие независимости случайных величин, и убедитесь, что значение ковариации в этом случае равно нулю.
Для того чтобы получить теоретическую корреляцию \( \rho_{XY} \) (\(\rho \) — буква греческого алфавита, читается «ро»), надо поделить ковариацию на среднеквадратические отклонения
\[ \rho_{XY}=\frac{R_{XY}}{\sqrt{D_X}\sqrt{D_Y}} \]
В нашем случае \( D_X=D_Y=2 \). Подставляя в формулу, получаем
\[ ρ_{XY}=0.3. \]
В общем случае для случайных величин, заданных таблицами
| X | x1 | x2 | … | xm | и | Y | y1 | y2 | … | ym |
| p1 | p2 | … | pm | q1 | q2 | … | qm |
теоретические ковариация и корреляция задаются формулами
\[ R_{XY}=\sum_{i,j}{(x_i-M_X)(y_j-M_Y)\cdot p(X=x_i , Y=y_j)} \]
\[ ρ_{XY}=\frac{R_{XY}}{σ_X σ_Y } \]
где \( σ_X=\sqrt{D_X},σ_Y=\sqrt{D_Y} \).
Замечание. Если вместо Y и y подставить в формулу ковариации X и x, соответственно, то формула ковариации превратится в формулу дисперсии X. Действительно, если i ≠ j, то \( p(X=x_i , X=x_j)=0 \), поскольку случайная величина не может одновременно принимать два разных значения; если \( i=j \), то \( p(X=x_i,X=x_i) \) тавтологично равно \( p(X=x_i) \). Таким образом, в формуле для ковариации будут отличны от нуля только «диагональные» члены, для которых \( i=j \), т.е.
\[R_{XX}=\sum_{(i=j)}(x_i-M_X)(x_j-M_X)p(X=x_i, X=x_j)=\sum_i(x_i-M_X )^2 p_i=D_X \].
9.2.3. Гипотезы, связанные с ненулевой теоретической корреляцией. Преобразование Фишера
В предыдущей главе обсуждались вопросы, связанные с противопоставлением гипотез о равенстве нулю или неравенстве нулю теоретической корреляции. В случае, если верна гипотеза \( H_0 \) о независимости переменных (тем самым их теоретическая корреляция равна нулю), выборочная корреляция принимает значения более или менее близкие к нулю. Большие отклонения от нуля рассматриваются как свидетельства в пользу альтернативной гипотезы.
Если же теоретическая корреляция случайных величин отлична от нуля, то задачи решаются с помощью преобразования Фишера. Наиболее распространенной из таких задач является задача сравнения корреляций. Например, проверка гипотезы о равенстве корреляций \( ρ_1=ρ_2 \) против альтернативы \( ρ_1\neqρ_2 \).
Напомним формулу выборочной корреляции. Пусть \( (x_1,…,x_n) \) и \( (y_1,…,y_n) \) — связанные выборки (в данном случае показатели с одинаковыми номерами принадлежат одному испытуемому).
Формула выборочной корреляции в наиболее часто употребляемом виде:
\[ r_{xy}=\frac{\frac{1}{n-1}\big((x_1-\overline{x} )(y_i-\overline{y})+…+(x_n-\overline{x})(y_n-\overline{y})\big)}{s_x s_y} \]
Если теоретическая корреляция двух переменных не равна нулю, то выборочная корреляция этих переменных будет варьировать от испытания к испытанию не вокруг нуля, а приблизительно вокруг этой теоретической корреляции.
Если размер выборок достаточно велик ( \( n>20 \)), то можно воспользоваться преобразованием Фишера.
Если корреляция реальных случайных величин, в результате испытаний которых были получены выборки \( (x_1,…,x_n) \) и \( (y_1,…,y_n) \), равна некоторому числу ρ, то распределение статистики (напомним, что статистика является случайной величиной)
\[ z_{xy}=\frac{1}{2}ln \bigg(\frac{1+r_{xy}}{1-r_{xy}}\bigg) \]
будет приближенно нормальным с математическим ожиданием
\[ M_z=\frac{1}{2}ln \bigg(\frac{1+ρ}{1-ρ}\bigg)+\frac{ρ}{2n-2} \]
и дисперсией
\[ D_z=\frac{1}{n-3} \]
Переход от \( r_{xy} \) к \( z_{xy} \) называется преобразованием Фишера.
Если мы теперь захотим, имея выборки \( (x_1,…,x_20) \) и \( (y_1,…,y_20) \), проверить гипотезу \( H_0 \) о том, что реальная корреляция ρ равна, скажем, 0.2, то эта гипотеза будет эквивалентна гипотезе о математическом ожидании преобразования Фишера от выборочной корреляции, рассмотренной как случайная величина. Результат этого преобразования — нормально распределенная случайная величина с математическим ожиданием
\[ \frac{1}{2}ln \bigg(\frac{1+0.2}{1-0.2}\bigg)+\frac{0.2}{2\cdot 20-2} \]
и дисперсией \( D_z=1/(20-3) \). Для проверки гипотез мы можем использовать квантили нормального распределения.
Особенно важное применение преобразования Фишера — сравнение двух выборочных коэффициентов корреляции. (Например, мы хотим исследовать вопрос, одинаковы ли корреляции между ростом и весом у жителей Москвы и Лиссабона.)
Пусть \( r_1 \) и \( r_2 \) выборочные коэффициенты корреляции, полученные по выборкам размера \( n_1 \) и \( n_2 \) соответственно.
Если реальные корреляции \( \rho_1 \) и \( \rho_2 \) равны, то случайная величина \( z_1-z_2 \) будет иметь нормальное распределение с математическим ожиданием, равным нулю, и дисперсией, равной сумме дисперсий \( D_1 \) и \( D_2 \), т.е.
\[ \frac{1}{n_1-3}+\frac{1}{n_2-3} \]
Тогда
\[ z_{1-2}=\frac{z_1-z_2}{\sqrt{\big(\frac{1}{(n_1-3}+\frac{1}{n_2-3}\big)}} \]
будет стандартной нормальной случайной величиной, и гипотеза о равенстве корреляций оценивается с помощью квантилей нормального распределения. В пользу неравенства будут свидетельствовать аномально большие (положительные или отрицательные) значения \( z_{1-2} \).
В SPSS и Jamovi такой расчет автоматически провести не удастся, но существует достаточно много онлайновых калькуляторов, позволяющих сравнить два коэффициента корреляции Пирсона, в качестве примера приведем ссылку на один из них: https://www.psychometrica.de/correlation.html
>> следующий параграф>>
[1] Для лучшего понимания рекомендуем ввести данные в SPSS, проделать регрессионный анализ и найти в таблицах вывода все полученные ниже числа. Однако мы здесь изложим эту важную тему компактно и без таблиц.
[2] Если быть совсем точным, то описание модели дисперсионного анализа в нашем случае таково: для центрированной системы шести чисел, разбитых на три группы по два, подобрать центрированную систему чисел для каждой из групп, чтобы сумма квадратов остатков была минимальной. Решение регулируется двумя параметрами (поскольку система трех чисел должна быть центрирована). Наилучшее приближение дает система средних групповых, которая является центрированной, поскольку центрирована исходная система шести точек.
[3] Мощность критерия измеряется вероятностью принять гипотезу \( H_1 \), когда она верна. В нашем случае она выше для регрессионного анализа, если гипотеза предполагает линейный рост знаний.