В этом параграфе мы предлагаем читателю ознакомиться с процедурой сравнения средних значений в статистическом пакете SPSS. Наиболее распространенный (и понятный) пример — это ситуация повторного измерения каких-либо психологических параметров у одних и тех же испытуемых, например, изменений этих параметров во времени (возрастных изменений или связанных с каким-либо экспериментальным воздействием).
Рассматриваемые ниже примеры представляют собой данные, реконструированные по отчетам о реальных исследованиях.
Пример 6.3(1). Расчет Т-критерия Стьюдента для связанных выборок в статистическом пакете SPSS.
Рассмотрим смоделированные данные исследования влияния алкоголя на время простой двигательной реакции. Эксперимент строился следующим образом. В начале у испытуемых измерялось фоновое время реакции: для этого им предъявляли визуальные стимулы и просили их как можно быстрее нажимать на кнопку при их предъявлении. При этом регистрировалось время, прошедшее от момента предъявления стимула до момента ответа испытуемого (в миллисекундах). Затем испытуемым вводили дозу алкоголя и спустя 20 минут проводили ту же пробу на время реакции повторно.
Результаты эксперимента приведены в файле ReactionTime.sav. Первый столбец (num) — это номер испытуемого, второй (rt1) — это среднее время реакции в 50 фоновых пробах, третий столбец (rt2) — это среднее время реакции в экспериментальных пробах (после приема алкоголя).
Проведем сравнение времени реакции в первой и второй пробе с помощью Т-критерия Стьюдента. Для вызова этой процедуры нужно выбрать в меню пункт Анализ — Сравнение средних — T-критерий для парных выборок (Analyze — Compare Means — Pared—Samples T—test). В появившемся окне необходимо задать по крайней мере одну пару сравниваемых переменных. В нашем случае это пара переменных rt1 — rt2. Переместим их в первую строку столбцов «Переменная1» (Variable1) и «Переменная2» (Variable2) соответственно. В случае, когда в исследовании есть несколько переменных, которые надо сравнить между собой, таких пар можно задать любое количество. После задания пар для сравнения нажмем кнопку ОК, после чего в окне вывода появится результат анализа. Таблица 6.3(2) содержит информацию об основных параметрах распределения сравниваемых переменных — средние значения, стандартное отклонение, стандартная ошибка среднего.
Таблица 6.3(2). Статистики парных выборок
| Статистика парных выборок | |||||
| Среднее | N | Станд. отклонения | Станд. средняя ошибка | ||
| Пара 1 | default reaction time | 222.1826 | 70 | 19.86946 | 2.37485 |
| reaction time after alcohol | 240.6045 | 70 | 29.12203 | 3.48075 | |
Как видно из таблицы, среднее значение времени реакции после приема алкоголя увеличивается больше, чем на 18 мс.
Нет смысла сравнивать это число со стандартным отклонением разности, чтобы оценить величину эффекта. Действительно, представим ситуацию, когда все участники эксперимента увеличили время реакции ровно на 19 мс. Тогда разность замеров была бы просто константой, т.е. имела бы нулевую дисперсию. Если иметь в виду содержательную задачу – понять, что значит 18 мс для нашей выборки (величина эффекта), эту разность средних имеет смысл сравнить со стандартным отклонением фонового времени реакции, которое равно 19.9. В таком случае мы получим, что среднее время реакции после приема алкоголя отклоняется от среднего фонового на 0.92 (\( 18.4/19.9\approx0.92 \)) стандартного отклонения. Это значит, например, что человек со средним фоновым временем реакции имеет сдвинутое алкоголем время реакции на уровне человека, быстрее которого примерно 4/5 (точнее — 81.6%) популяции, а 1/5 – медленнее (см. таблицу нормального распределения в подпараграфе 4.1.3). Много это или мало — вопрос практический, а не статистический.
Статистическую значимость различий средних позволяют оценить результаты расчета Т-критерия, приведенные в таблице 6.3(3).
Таблица 6.3(3). Критерий парных выборок
| Парные разности | t | ст.св. | Знч. (2-ст.) | ||||||
| Средн. | Стд. откл. | Стд. ошибка средн. | 95% доверительный интервал разности средних | ||||||
| Нижняя граница | Верхняя граница | ||||||||
| Пара 1 | default reaction time — reaction time after alcohol | −18.42 | 19.57 | 2.34 | −23.09 | −13.75 | −7.876 | 69 | 0.000 |
В начале этой таблицы приведены значения параметров распределения разностей оцениваемых переменных. Стандартная ошибка среднего получается делением стандартного отклонения среднего на \( \sqrt{n} \), далее помещены доверительные интервалы разности (относительно полученной точечной оценки математического ожидания («истинного» среднего) замедления реакции при приеме алкоголя в генеральной совокупности), равной -18.4, строится интервальная оценка положения математического ожидания – предположительно оно лежит в интервале от -23.1 до -13.75, подробнее о доверительных интервалах см. раздел 5.1.2), t-статистика Стьюдента есть результат деления средней разности на стандартную ошибку. В нашем случае t = −7.876. Следующий столбец содержит количество степеней свободы. Так как в эксперименте приняло участие 70 человек, количество степеней свободы в данном случае равно 69. Наконец, последний столбец — это двухсторонняя значимость полученного значения t. В таблице стоит число 0.000. Принимая во внимание округление, можно быть уверенными, что значимость результата меньше 0.0005. Однако есть способ получить более точное значение в таблице. Надо сделать двойной клик левой кнопкой мыши на само это число, что переведет таблицу в режим редактирования (кстати, в этом режиме можно редактировать подписи и т.п.), а затем сделать на это же число еще раз двойной клик. В результате появится более точное число. В нашем случае оно равно 0.000069. Так как значимость близка к нулю, мы можем вполне уверенно отвергнуть нулевую гипотезу и принять альтернативную, т.е. сделать вывод о том, что время реакции изменяется после приема алкоголя. Отчет о результате может выглядеть так: «Т-критерий Стьюдента для связанных выборок показал различие времени реакции в двух экспериментальных сериях (\( t(69) = -7.876,p < 0.0005 \)). Средний сдвиг равен 18.4 мс и составляет 0.92 от стандартного отклонения фоновых значений времени реакции, равного 19.86».
Пример 6.3(1)j. Расчет Т-критерия Стьюдента для связанных выборок в статистическом пакете Jamovi.
Рассмотрим смоделированные данные исследования влияния алкоголя на время простой двигательной реакции. Эксперимент строился следующим образом. В начале у испытуемых измерялось фоновое время реакции: для этого им предъявляли визуальные стимулы и просили их как можно быстрее нажимать на кнопку при их предъявлении. При этом регистрировалось время, прошедшее от момента предъявления стимула до момента ответа испытуемого (в миллисекундах). Затем испытуемым вводили дозу алкоголя и спустя 20 минут проводили ту же пробу на время реакции повторно.
Результаты эксперимента приведены в файле ReactionTime.sav. Первый столбец (num) — это номер испытуемого, второй (rt1) — это среднее время реакции в 50 фоновых пробах, третий столбец (rt2) — это среднее время реакции в экспериментальных пробах (после приема алкоголя).
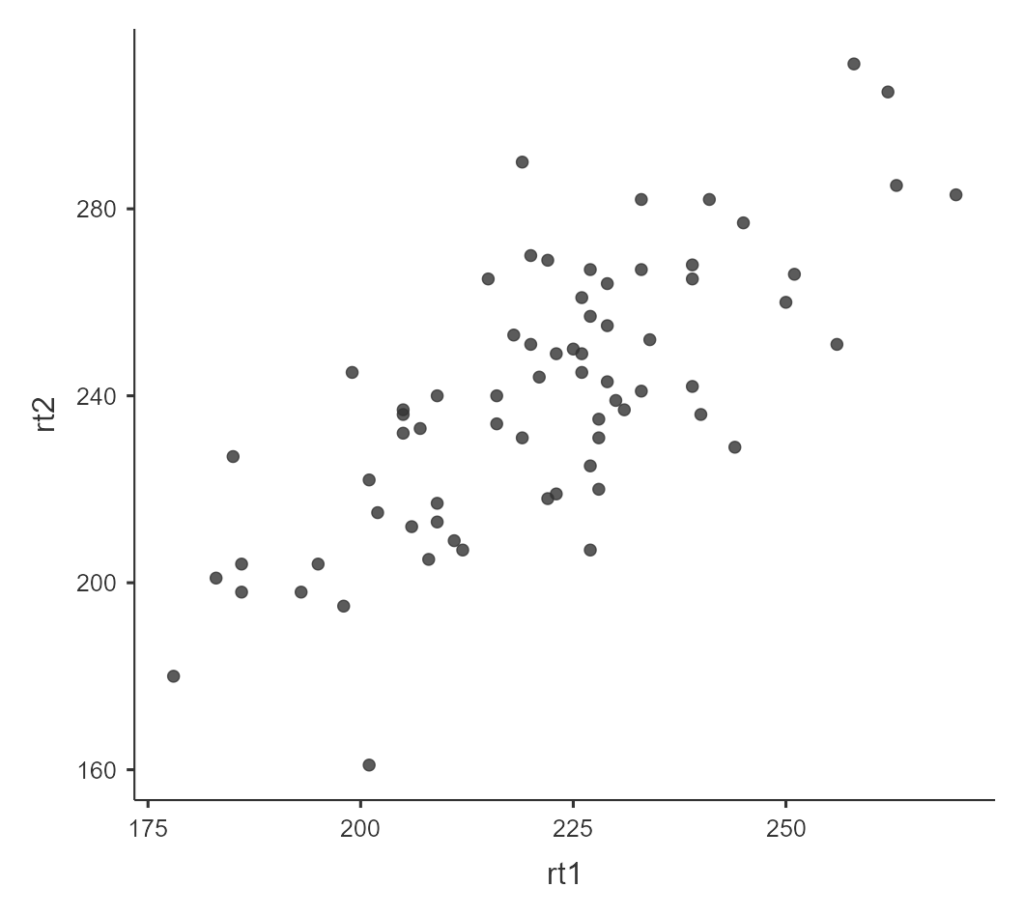
Посмотрим на распределение времен реакции до и после приема алкоголя и рассчитаем коэффициент корреляции Пирсона для предварительной оценки применимости Т-критерия. Для этого выбираем меню Analyses – Exploration – Scatterplot[6] и в появившемся окне переносим rt1 на ось Х и rt2 на ось Y, чтобы получить диаграмму рассеивания, и в меню Analyses – Regression – Correlation Matrix переносим те же переменные в правую форму для расчета коэффициента корреляции. Диаграмма рассеивания на Рисунке 6.3(2)j показывает сильную положительную связь между результатами первого и второго замеров, о том же говорит полученный коэффициент корреляции Пирсона (r = 0.742, p < 0.001). Время реакции в двух замерах хорошо согласовано, а значит применение Т-критерия Стьюдента уместно.
Рисунок 6.3.(2)j. Диаграмма рассеивания переменных rt1 и rt2
Проведем сравнение времени реакции в первой и второй пробе с помощью Т-критерия Стьюдента. Для этого идем в меню Analyses – T—tests – Paired—Samples T—Test. В появившемся окне необходимо задать по крайней мере одну пару сравниваемых переменных. В нашем случае это пара переменных rt1 — rt2. Переместим их в правое окно Paired Variables так, чтобы они оказались в одной строке. В случае, когда в исследовании есть несколько переменных, которые надо сравнить между собой, таких пар можно задать любое количество. Для полноты описания результатов выберите дополнительные параметры обработки, см. меню на рисунке 6.3(3j):
Рисунок 6.3(3)j. Меню t-критерия Стьюдента при сравнении парных выборок (настройки по умолчанию)
Tests: Если отметить пункт Wilcoxon rank, или критерий знаковых рангов Вилкоксона (см. главу 11.1.1). Тест выдает значение и уровень значимости непараметрического аналога t-критерия.
В разделе Additional Statistics можно включить следующие дополнительные статистики:
- Mean difference – описательные статистики для распределения разностей (среднее, стандартная ошибка среднего), Confidence interval – доверительный интервал для среднего при выбранном уровне доверия (по умолчанию – 95%).
- Effect size, или оценка величины эффекта t-критерия (в данном случае используется коэффициент d Коэна, см. приложение 4.3). Confidence interval – доверительный интервал для величины эффекта при выбранном уровне значимости.
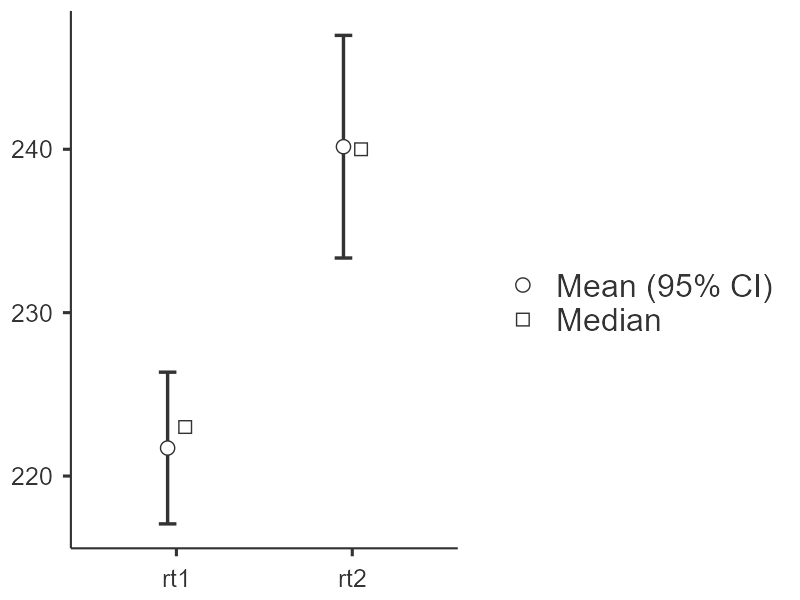
- Descriptives (plots) выводит описательные статистики для выборок по отдельности (N — количество наблюдений, Mean — среднее значение, Median — медиана, SD — стандартное отклонение и SE — стандартная ошибка среднего). Те же показатели отражены на графике, стандартная ошибка среднего использована для построения доверительных интервалов для двух выборок. Знание о распределениях выборок по отдельности полезно для оценки пригодности t-критерия.
Assumption Checks: Normality test, или Тест Шапиро-Уилка используется для оценки соответствия распределения разностей нормальному закону (подробнее об ограничениях T–критерия см. параграф 6.2.1.). Отклонение от нормального закона – повод внимательно рассмотреть особенности распределения разностей и возможные причины отклонения. Q-Q plot позволяет провести сравнение распределения разностей с нормальным в графической форме.
Hypothesis: выбор между направленными и ненаправленными гипотезами, то есть применение 1-стороннего или 2-стороннего T-критерия. Без содержательных оснований для перехода к односторонней гипотезе лучше оставить значение по умолчанию.
Missing values: выбор между исключением из анализа наблюдений с пропущенными значениями для каждой пары переменных в отдельности (Exclude cases by analysis), либо всей строки целиком, если хоть одно значение отсутствует (Exclude cases listwise).
Добавим в анализ критерий Вилкоксона, тест Шапиро-Уилка, описательные статистики для средней разности и величины эффекта с доверительными интервалами. В появившемся справа окне вывода обновляются результаты анализа. Рассмотрим их последовательно: тест Шапиро-Уилка, как и другие тесты нормальности, не находит отклонений распределения разностей от нормального закона (W = 0.990, p = 0.856) (см. таблицу 6.3(4)j), что является еще одним из обоснований применимости t-критерия Стьюдента.
Таблица 6.3(4)j. Результаты тестов на нормальность: Шапиро-Уилк, Колмогоров-Смирнов и Андерсон-Дарлин
| Tests of Normality | |||||||||
| statistic | p | ||||||||
| default reaction time | reaction time after alcohol | Shapiro-Wilk | 0.990 | 0.856 | |||||
| Kolmogorov-Smirnov | 0.059 | 0.970 | |||||||
| Anderson-Darling | 0.217 | 0.836 | |||||||
| Note. Additional results provided by moretests | |||||||||
Описательные статистики, приведенные в таблице 6.3(5)j, и график выборок по отдельности, представленный на рисунке 6.3(6)j, говорят о более высокой дисперсии результатов второго замера (rt2) по сравнению с результатами первого замера (rt1), применению критерия Стьюдента это не мешает.
Таблица 6.3(5)j. Описательные статистики для выборок rt1 и rt2
| Descriptives | |||||||||||
| N | Mean | Median | SD | SE | |||||||
| default reaction time | 70 | 221.714 | 223.000 | 19.817 | 2.369 | ||||||
| reaction time after alcohol | 70 | 240.157 | 240.000 | 29.083 | 3.476 | ||||||
Рисунок 6.3(6)j. График средних по выборкам. ○ – среднее, □ – медиана, усами отмечены доверительные интервалы для среднего
Таблица 6.3(7)j. Результаты t-критерия Стьюдента для парных выборок
| Paired Samples T-Test | |||||||||||||||||||||||
| 95% Confidence Interval | |||||||||||||||||||||||
| Statistic | df | p | Mean difference | SE difference | Lower | Upper | Effect Size | ||||||||||||||||
| rt1 | rt2 | Student’s t | -7.878 | 69.000 | < .001 | -18.443 | 2.341 | -23.113 | -13.773 | Cohen’s d | -0.942 | ||||||||||||
| Wilcoxon W | 213.500 | < .001 | -18.500 | 2.341 | -23.000 | -13.500 | Rank biserial correlation | -0.828 | |||||||||||||||
Как видно из таблицы 6.3(7)j, среднее значение времени реакции после приема алкоголя увеличивается больше, чем на 18 мс (Mean difference), стандартная ошибка оценки среднего составляет 2.3 мс (SE difference), далее помещены доверительные интервалы разности (относительно полученной точечной оценки математического ожидания («истинного» среднего) замедления реакции при приеме алкоголя в генеральной совокупности), равной -18.4, строится интервальная оценка положения математического ожидания – предположительно оно лежит в интервале от -23.1 до -13.8, подробнее о доверительных интервалах см. раздел 5.1.2), t-статистика Стьюдента есть результат деления средней разности на стандартную ошибку. В нашем случае t = −7.878 (Statistic) при 69 степенях свободы (df = N — 1). Двухсторонняя значимость полученного значения t составляет p < 0.001 (можно увеличить точность отображения значимостей в меню программы, тогда отобразится значение p = 0.000000000033). Так как значимость близка к нулю, мы можем вполне уверенно отвергнуть нулевую гипотезу и принять альтернативную, т.е. сделать вывод о том, что время реакции изменилось после приема алкоголя. Аналогичный вывод может быть сделан на основе критерия Вилкоксона.
Изменение скорости реакции, измеренное в миллисекундах, не позволяет понять, сильное это изменение или нет, нужна универсальная шкала оценки величины эффекта. Для выбора единиц, относительно которых можно было бы стандартизовать полученные 18 мс, мы воспользуемся двумя альтернативными способами рассуждения. Первый говорит, что нет смысла сравнивать среднюю разность со стандартным отклонением разностей, чтобы оценить величину эффекта. Действительно, представим ситуацию, когда все участники эксперимента увеличили время реакции ровно на 18 мс. Тогда разность замеров была бы просто константой, т.е. имела бы нулевую дисперсию. Если иметь в виду содержательную задачу – понять, что значит 18 мс для нашей выборки, эту разность средних имеет смысл сравнить со стандартным отклонением фонового времени реакции, которое равно 19.8. В таком случае мы получим, что среднее время реакции после приема алкоголя отклоняется от среднего фонового времени на 0.65 (18.4/19.8≈0.92) стандартного отклонения. Это значит, например, что человек со средним фоновым временем реакции имеет сдвинутое алкоголем время реакции на уровне человека, быстрее которого примерно 4/5 популяции, а пятая часть – медленнее (см. таблицу нормального распределения в подпараграфе 4.1.3). Много это или мало — вопрос практический, а не статистический. Тем не менее, идентичный сдвиг значений маловероятен, так как физиологическая реакция на алкоголь у людей разная, и в Jamovi реализована другая логика рассуждения: величина эффекта учитывает дисперсию индивидуальных реакций на алкоголь и ее оценка вычисляется как отношение величины разности к стандартному отклонению разностей (d Коэна = 0.942). Величину стандартного отклонения разностей можно восстановить из представленной в таблице стандартной ошибки по формуле: \( SD = SE*\sqrt{N} \).
Отчет о результате может выглядеть так: «t-критерий Стьюдента для связанных выборок показал увеличение времени реакции в результате приема алкоголя (t(69) = −7.878, p < 0.001), средний сдвиг равен 18.4 мс и составляет 0.942 от стандартного отклонения разностей времени реакции, равного 19.59 мс».
Пример 6.3(1)r. Расчет Т-критерия Стьюдента для связанных выборок в R.
Рассмотрим смоделированные данные исследования влияния алкоголя на время простой двигательной реакции. Эксперимент строился следующим образом. В начале у испытуемых измерялось фоновое время реакции: для этого им предъявляли визуальные стимулы и просили их как можно быстрее нажимать на кнопку при их предъявлении. При этом регистрировалось время, прошедшее от момента предъявления стимула до момента ответа испытуемого (в миллисекундах). Затем испытуемым вводили дозу алкоголя и спустя 20 минут проводили ту же пробу на время реакции повторно.
Результаты эксперимента приведены в файле ReactionTime.sav. Первый столбец (num) — это номер испытуемого, второй (rt1) — это среднее время реакции в 50 фоновых пробах, третий столбец (rt2) — это среднее время реакции в экспериментальных пробах (после приема алкоголя).
Проведем сравнение времени реакции в первой и второй пробе с помощью Т-критерия Стьюдента с помощью функции t.test. При сравнении двух выборок они должны быть первыми двумя аргументами функции. Также при сравнении связанных выборок необходимо указать аргумент paired = TRUE (иначе, о умолчанию, будет рассчитан t-критерий для несвязанных выборок). Если таблица данных с временами реакций называется data_rt, то соответствующая команда будет выглядеть так:
t.test(data_rt$rt1, data_rt$rt2)
Результат анализа будет следующим:
Paired t-test data: data_rt$rt1 and data_rt$rt2 t = -7.878, df = 69, p-value = 3.342e-11 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -23.11316 -13.77256 sample estimates: mean of the differences -18.44286.
В начале приводится статистика t-критерия, который в данном случае равен -7.878. Далее приведено число степеней свободы. Так как в эксперименте приняло участие 70 человек, оно в данном случае равно 69. и значимость, которая в данном случае очень близка к нулю. Коротко этот результат можно записать как t(69) = -7.878, p<0.001. Далее приводится статистика разности средних времени реакции в двух выборок – 95% доверительный интервал разности средних [-23.11316 -13.77256] и точечная оценка – разность средних, равная 18. 44286.
Таким образом видно, что среднее значение времени реакции после приема алкоголя увеличивается больше, чем на 18 мс.
Нет смысла сравнивать это число со стандартным отклонением разности[7], чтобы оценить величину эффекта. Действительно, представим ситуацию, когда все участники эксперимента увеличили время реакции ровно на 19 мс. Тогда разность замеров была бы просто константой, т.е. имела бы нулевую дисперсию. Если иметь в виду содержательную задачу – понять, что значит 18 мс для нашей выборки (величина эффекта), эту разность средних имеет смысл сравнить со стандартным отклонением фонового времени реакции, которое равно 19.9 (рассчитать его можно командой sd(data_rt$rt1)). В таком случае мы получим, что среднее время реакции после приема алкоголя отклоняется от среднего фонового на 0.92 (18.4/19.9≈0.92) стандартного отклонения. Это значит, например, что человек со средним фоновым временем реакции имеет сдвинутое алкоголем время реакции на уровне человека, быстрее которого примерно 4/5 (точнее — 81.6%) популяции, а 1/5 – медленнее (см. таблицу нормального распределения в подпараграфе 4.1.3). Много это или мало — вопрос практический, а не статистический.
Остановимся подробнее на доверительном интервале разности (относительно полученной точечной оценки математического ожидания («истинного» среднего) замедления реакции при приеме алкоголя в генеральной совокупности), равной -18.4, строится интервальная оценка положения математического ожидания – предположительно оно лежит в интервале от -23.1 до -13.75, подробнее о доверительных интервалах см. раздел 5.1.2), t-статистика Стьюдента есть результат деления средней разности на стандартную ошибку среднего. В нашем случае, напомним t = −7.878. В целом, отчет о результате проведенного анализа может выглядеть так: «Т-критерий Стьюдента для связанных выборок показал различие времени реакции в двух экспериментальных сериях (t(69)=−7.878, p<0.0001). Средний сдвиг равен 18.4 мс и составляет 0.92 от стандартного отклонения фоновых значений времени реакции, равного 19.86».
Пример 6.3(4). В файле Ego.sav (версия для SPSS, версия для Jamovi) содержатся данные, моделирующие результаты исследований, проведенных на основе теории Дж. Левинджер[1]. В теоретической модели Левинджер выделяется ряд последовательных стадий развития эго, которые диагностируются при помощи методики неоконченных предложений. Диапазон изменения оценки развития эго от двух[2] (импульсивная стадия) до девяти (стадия интеграции). В исследовании, проведенном в рамках этой концепции, испытуемых, учеников 10-го класса просили заполнить методику неоконченных предложений Вашингтонского университета. Эксперты рассчитывали средний уровень развития эго. Через пять лет (на четвертом курсе) тех же испытуемых просили заполнить методику повторно. Задачей исследования было выявить, переходят ли с возрастом испытуемые на более высокие уровни развития эго. В файле первый столбец содержит полученные оценки уровня развития эго в 10-м классе, во втором — оценки уровня эго на четвертом курсе.
Упражнение 6.3(5). Проверьте, есть ли изменения в уровне развития эго с возрастом. Оцените значимость с помощью Т—критерия Стьюдента
Пример 6.3(6). Файл IllnessSelf.sav (версия для SPSS, версия для Jamovi) содержит данные, полученные с помощью методики, в основе которой лежит понятие самоэффективности А. Бандуры[3].
В модели А. Бандуры самоэффективность — уверенность человека в своих силах достичь какой-либо цели. Самоэффективность в отношении болезни — уверенность человека в своих возможностях справиться с болезнью, вылечиться или (в случае хронического заболевания) — сохранять привычный уровень активности и круг интересов, несмотря на заболевание.
В исследовании оценивалась ретестовая надежность методики оценки самоэффективности в отношении болезни — устойчивость показателей с течением времени. Один из аспектов анализа устойчивости — оценка различий средних баллов выборки испытуемых при первом и втором замере. В файле приведены данные здоровых испытуемых, дважды отвечавших на вопросы методики с интервалом в три недели.
Упражнение 6.3(7). Проведите оценку изменения показателей испытуемых по двум замерам методики при помощи Т-критерия Стьюдента для связанных выборок. Подумайте, в каких единицах следует измерять степень (не)надежности методики. Проведите вычисления.
Далее мы рассмотрим T-критерий Стьюдента для независимых выборок. Как уже говорилось выше, критерий используется для решения задачи сравнения какого-либо показателя, представленного в интервальной шкале, у двух групп испытуемых. При этом группы являются независимыми, т.е. испытуемые, входящие в первую группу, и испытуемые во второй группе — разные люди. Примером таких задач может быть сравнение интеллекта у мужчин и женщин, сравнение успеваемости у школьников двух параллельных классов, сравнение выраженности нарушений мышления у больных шизофренией и в группе нормы.
Пример 6.3(8). Расчет Т-критерия для независимых выборок
Данные, представленные в файле Neuro.sav, — результаты эксперимента, проводившегося в лаборатории нейропсихологии МГУ имени М.В. Ломоносова. Исследовалась взаимосвязь между уровнем успеваемости детей в школе и состоянием их нейропсихологических функций, связанных с так называемым энергетическим блоком мозга (по А.Р. Лурии). Состояние нейропсихологической функции измерялось с помощью методики быстрого автоматизированного называния[4] — испытуемым предлагались наборы различных объектов для называния, их задача состояла в как можно более быстром назывании объектов. Предполагается, что чем быстрее испытуемый справляется с заданием, тем лучше у него развиты нейропсихологические функции, отвечающие за общую активацию.
В файле Neuro.sav приведены результаты проведения описанной методики у младших школьников. Дети были поделены на две группы — хорошо успевающих и отстающих, второй столбец (group) содержит код группы, к которой отнесен каждый испытуемый, «0» обозначает отстающих, «1» — хорошо успевающих. Далее представлены времена выполнения трех проб: называние цифр, называние осмысленных изображений и называние цветов (переменные numbers, figures и colors соответственно). Время измерялось в секундах.
Исследователи предполагали, что среднее время выполнения проб может различаться у двух выделенных групп детей: отстающие справятся с заданием за большее время, чем хорошо успевающие.
Сравним средние значения с помощью Т-критерия Стьюдента для несвязанных выборок. Для этого в меню надо выбрать пункт Анализ — Сравнение средних — T-критерий для независимых выборок (Analize — Compare means — Independent—Sample T—test). В появившемся диалоговом окне в поле Проверять переменные (Test Variable(s)) необходимо внести переменные, значения которых сравниваются у двух групп. Перенесем в окно переменную numbers (в это окно можно переносить сколько угодно переменных одновременно). В поле Группировать по (Grouping Variable) следует внести переменную group, кодирующую принадлежность испытуемых к той или иной группе. Затем, нажав кнопку Задать группы (Define groups) необходимо указать номера двух сравниваемых групп, в нашем случае это 0 и 1. Это дополнительное окно важно при попарном сравнении нескольких экспериментальных групп — в этом случае можно последовательно задавать различные пары для сравнения средних.
Таблица 6.3(9). Групповые статистики
| Группа | N | Среднее | Стд. отклонение | Стд. ошибка среднего | |
| Проба «цифры» — время выполнения | отстающие | 15 | 38.9627 | 8.85589 | 2.28658 |
| хорошо успевающие | 15 | 28.9627 | 6.07397 | 1.56829 |
После нажатия кнопки ОК в окне вывода появляются результаты расчетов. Первая таблица содержит информацию о размере групп (столбец N), среднем значении, стандартном отклонении и стандартной ошибке сравниваемых параметров в двух экспериментальных группах (таблица 6.3(9)).
Если обратить внимание на средние показатели времени выполнения проб в двух группах, то становится видно, что отстающие справлялись с заданием за большее время, чем дети из группы нормально успевающих: среднее время в секундах составило 38.96 и 28.96 соответственно. На вопрос об оценке значимости гипотез отвечает таблица 6.3(10). Рассмотрим ее подробнее (для компактности таблица сжата по горизонтали по сравнению с тем видом, который она имеет в окне вывода SPSS).
Таблица 6.3(10). T-критерий для независимых выборок
| Критерий равенства дисперсий Ливиня | t-критерий равенства средних | |||||||||
| 95% доверительный интервал разности средних | ||||||||||
| F | Знч. | t | ст. св. | Значимость (2-сторонняя) | Разность средних | Стд. ошибка разности | Нижняя граница | Верхняя граница | ||
| Проба «цифры» — время выполнения | Предполагается равенство
дисперсий |
4.412 | .045 | 3.607 | 28 | .001 | 10.00 | 2.77272 | 4.32033 | 15.67967 |
| Равенство дисперсий не предполагается | 3.607 | 24.785 | .001 | 10.00 | 2.77272 | 4.28696 | 15.71304 | |||
В SPSS Т-критерий для независимых выборок рассчитывается всегда в двух вариантах: предполагающем равенство дисперсий показателей сравниваемого параметра в двух группах и не предполагающем равенство дисперсий. В данном случае дисперсии практически равны и результаты в двух строках почти не различаются. Мы уже указывали, что всегда можно использовать строку Равенство дисперсий не предполагается (Equal of variances not assumed) (см. подпараграф 6.2.2). Чаще всего результаты двух вариантов различаются мало. В следующем примере 6.3(13) мы продолжим обсуждение этой темы.
Столбец t содержит результат расчета t-статистики, далее приведены соответствующие степени свободы (при неравенстве дисперсий число степеней свободы перестает измеряться целым числом). Столбец Знч. (Sig.) содержит значимость полученного значения t-статистики, в данном случае она равна 0.001. Именно этой значимостью оцениваются различия среднего времени выполнения проб, характеризующих состояния энергетического блока мозга испытуемыми двух групп. Кратко результаты применения Т-критерия можно записать так: \( t(28)=3.607,p=0.001 \).
В таблице приведена не только разность средних, которая равна 10 секундам, но и 95%-й доверительный интервал для разности: от 4.29 до 15.71 секунд — это напоминает нам, что 10 секунд — лишь оценка различия средних. Остается, однако, вопрос, что значат эти секунды с точки зрения различия развития функций.
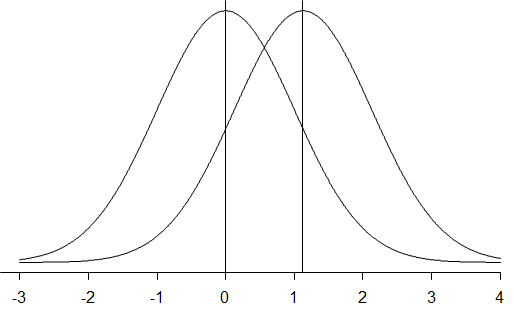
На этот вопрос отвечают, оценивая величину эффекта (SPSS ее не рассчитывает). В данном случае разумная мера — отношение разности средних к некоему среднему стандартному отклонению выборок (квадратному корню из средней дисперсии). Выборочные дисперсии также приходится вычислять вручную, возводя в квадрат стандартные отклонения 8.85589 и 6.07397. Средняя дисперсия равна 57.66, корень из нее – 7.59, а 10/7.59=1.317. Это и есть величина эффекта[5], которую в данном случае точнее называть мерой различия групп: средние по группам различаются на 1.317 стандартных отклонения. Некоторую визуализацию этой оценки дает рис. 6.3(11).
Рис. 6.3(11). Так выглядели бы два нормальных распределения, средние которых отличаются на 1.125 стандартных отклонения. По аналогии можно представлять себе соотношение распределений характеристики недоразвития энергетического блока мозга (чем больше время на выполнение задания, тем хуже = слева успевающие, справа отстающие).
Пример 6.3(8)j. Расчет Т-критерия для независимых выборок
Данные, представленные в файле Neuro.sav, — результаты эксперимента, проводившегося в лаборатории нейропсихологии МГУ имени М.В. Ломоносова. Исследовалась взаимосвязь между уровнем успеваемости детей в школе и состоянием их нейропсихологических функций, связанных с так называемым энергетическим блоком мозга (по А.Р. Лурии). Состояние нейропсихологической функции измерялось с помощью методики быстрого автоматизированного называния[4] — испытуемым предлагались наборы различных объекты, которые нужно было как можно быстрее называть. Предполагается, что чем быстрее испытуемый справляется с заданием, тем лучше у него развиты нейропсихологические функции, отвечающие за общую активацию.
В файле Neuro.sav приведены результаты проведения описанной методики у младших школьников. Дети были поделены на две группы — хорошо успевающих и отстающих, второй столбец (group) содержит код группы, к которой отнесен каждый испытуемый, «0» обозначает отстающих, «1» — хорошо успевающих. Далее представлены времена выполнения трех проб: называние цифр, называние осмысленных изображений и называние цветов (переменные numbers, figures и colors соответственно). Время измерялось в секундах.
Исследователи предполагали, что среднее время выполнения проб может различаться у двух выделенных групп детей: отстающие справятся с заданием за большее время, чем хорошо успевающие.
Сравним средние значения с помощью Т-критерия Стьюдента для несвязанных выборок. Для этого в меню надо выбрать пункт Analyses — T-Tests — Independent Samples T–Test). В появившемся диалоговом окне нужно перенести переменные, значения которых сравниваются у двух групп в поле “Dependent Variables” (Зависимые переменные). Перенесем в окно переменную numbers (в это окно можно переносить сколько угодно переменных одновременно). В поле “Grouping Variable” (Группирующая переменная) следует перенести переменную, кодирующую принадлежность испытуемых к одной из двух групп, в нашем случае это переменная group. Если группирующая переменная принимает больше двух значений, необходимо отобрать сравниваемые два уровня с помощью фильтра (см. Приложение 1.2). Для полноты описания результатов выберите дополнительные параметры обработки, см. меню на рисунке 6.3(9)j:
Рис. 6.3(9)j. Меню t-критерия Стьюдента при сравнении независимых выборок (настройки по умолчанию)
Tests:
- Welch‘s, или поправка Уэлча, используется в том случае, когда дисперсии в выборках неоднородны.
- Mann-Whitney U, или критерий Манна-Уитни (см. главу 1.2) выдает значение и уровень значимости непараметрического аналога t-критерия.
В разделе Additional Statistics можно включить следующие дополнительные статистики:
- Mean difference – описательные статистики для разности средних (разность, стандартная ошибка разности), Confidence interval – доверительный интервал для разности при выбранном уровне доверия (по умолчанию – 95%).
- Effect size, или оценка величины эффекта t-критерия (в данном случае используется коэффициент d Коэна, см. Приложение 4.3). Confidence interval – доверительный интервал для величины эффекта при выбранном уровне значимости.
- Descriptives (plots) выводит описательные статистики для выборок по отдельности (N — количество наблюдений, Mean — среднее значение, Median — медиана, SD — стандартное отклонение и SE — стандартная ошибка среднего). Те же показатели отражены на графике, стандартная ошибка среднего использована для построения доверительных интервалов для двух выборок.
Assumption Checks: Homogeneity test, или Критерий однородности дисперсий Ливиня, используется для оценки различий между дисперсиями в группах. Разница в дисперсиях может быть интересным самостоятельным результатом (одно из условий дает проявиться индивидуальным различиям в большей степени), но также может указывать на наличие выбросов в одной из выборок, требующих фильтрации массива данных. Неоднородность дисперсий снижает надежность результатов Т-критерия и требует введения поправки Уэлча (Welch’s в разделе Tests). Jamovi в любом случае делает расчет теста Ливиня и добавляет комментарий к значению Т-критерия, если обнаруживает неоднородность.
Normality test, или Тест Шапиро-Уилка используется для оценки соответствия распределения разностей нормальному закону.
Hypothesis: выбор между направленными и ненаправленными гипотезами, то есть применение 1-стороннего или 2-стороннего T-критерия. Без содержательных оснований для перехода к односторонней гипотезе лучше оставить значение по умолчанию.
Missing values: выбор между исключением из анализа наблюдений с пропущенными значениями для каждой пары переменных в отдельности (Exclude cases analysis by analysis), либо всей строки целиком, если в ней отсутствует хотя бы одно значение (Exclude cases listwise).
Добавим в анализ критерий Манна-Уитни, тест однородности дисперсий, описательные статистики для разности средних и величины эффекта. Рассмотрим полученные результаты.
Таблица 6.3(10)j. Результаты t-критерия Стьюдента для независимых выборок
| Independent Samples T-Test | |||||||||||||||||
| Statistic | df | p | Mean difference | SE difference | Effect Size | ||||||||||||
| numbers | Student’s t | 3.607 | ᵃ | 28.000 | 0.001 | 10.000 | 2.773 | Cohen’s d | 1.317 | ||||||||
| Welch’s t | 3.607 | 24.785 | 0.001 | 10.000 | 2.773 | Cohen’s d | 1.317 | ||||||||||
| Mann-Whitney U | 39.000 | 0.002 | 9.370 | Rank biserial correlation | 0.653 | ||||||||||||
| ᵃ Levene’s test is significant (p < .05), suggesting a violation of the assumption of equal variances | |||||||||||||||||
Из Таблицы 6.3(10)j узнаем, что разность средних значений времени называния чисел составляет 10 секунд при стандартной ошибке разности в 2.8 сек., эти различия значимы, однако программа предупреждает нас о том, что дисперсии в выборках не равны. Посмотрим на таблицу с описательными статистиками по группам (6.3(11)j) и на результаты критерия проверки однородности дисперсий Ливиня (6.3(12)j).
Таблица 6.3(11)j. Описательные статистики
| Group Descriptives | |||||||||||||
| Group | N | Mean | Median | SD | SE | ||||||||
| numbers | отстающие | 15 | 38.963 | 37.590 | 8.856 | 2.287 | |||||||
| хорошо успевающие | 15 | 28.963 | 28.000 | 6.074 | 1.568 | ||||||||
Таблица 6.3(12)j. Результаты проверки однородности дисперсий
| Homogeneity of Variances Test (Levene’s) | |||||||||
| F | df | df2 | p | ||||||
| numbers | 4.412 | 1 | 28 | 0.045 | |||||
| Note. A low p-value suggests a violation of the assumption of equal variances | |||||||||
Описательные статистики позволяют определить, что в группах по 15 человек, хорошо успевающие дети называют числа быстрее отстающих (первым нужно в среднем чуть меньше 29 секунд, вторым – чуть меньше 39 секунд). Различия между отстающими детьми больше, чем между хорошо успевающими (стандартное отклонение в 8.856 сек против 6.074), на неоднородность дисперсий указывает критерий Ливиня (F(1,28) = 4.412, p = 0.045).
Упражнение 6.3(13)j. С помощью меню Descriptives выведите гистограммы для обеих групп и определите, из-за чего возникает разница в дисперсиях. Например, нет ли в одной из групп экстремального значения (выброса), который искажал бы общую картину различий между детьми.
Неоднородность дисперсий требует применить поправку Уэлча, получаем следующее описание различий в скорости называния чисел: «Хорошо успевающие дети называют числа в среднем на 10 секунд быстрее отстающих, эти различия значимы согласно t-критерию Стьюдента с поправкой Уэлча (t(24.785) = 3.607, p = 0.001)».
Остается дополнить описание значимости различий данными о величине эффекта. В данном случае разумная мера величины эффекта — это отношение разности средних к некоему среднему стандартному отклонению выборок (квадратному корню из средней дисперсии). Для выборок одинакового объема, как в нашем случае, формула для d Коэна выглядит очень просто:
\[ \frac{\overline{x_1}-\overline{x_2}}{\sqrt{\frac{s^2_{x1}+s^2_{x2}}{2}}} \]
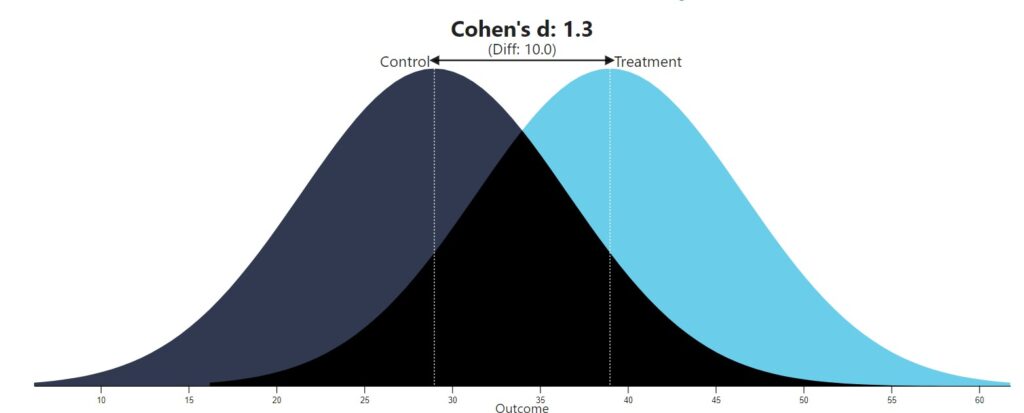
Получаем значение d Коэна = 1.317, то есть разрыв между детьми из разных групп большой и составляет 1.3 стандартных отклонения. Результат, смоделированный на нормальных распределениях, показан на рисунке 6.3(14)j.
Рис. 6.3(14)j. Так выглядели бы два нормальных распределения, средние которых отличаются на 1.317 стандартных отклонения. По аналогии можно представить себе соотношение распределений характеристики недоразвития энергетического блока мозга (слева успевающие, справа – отстающие, с большей дисперсией, чем в первой группе, то есть распределение более плоское).
Пример 6.3(8)r. Расчет Т-критерия для независимых выборок
Данные, представленные в файле Neuro.sav, — результаты эксперимента, проводившегося в лаборатории нейропсихологии МГУ имени М.В. Ломоносова. Исследовалась взаимосвязь между уровнем успеваемости детей в школе и состоянием их нейропсихологических функций, связанных с так называемым энергетическим блоком мозга (по А.Р. Лурии). Состояние нейропсихологической функции измерялось с помощью методики быстрого автоматизированного называния[4] — испытуемым предлагались наборы различных объектов для называния, их задача состояла в как можно более быстром назывании объектов. Предполагается, что чем быстрее испытуемый справляется с заданием, тем лучше у него развиты нейропсихологические функции, отвечающие за общую активацию.
В файле Neuro.sav приведены результаты проведения описанной методики у младших школьников. Дети были поделены на две группы — хорошо успевающих и отстающих, второй столбец (group) содержит код группы, к которой отнесен каждый испытуемый, «0» обозначает отстающих, «1» — хорошо успевающих. Далее представлены времена выполнения трех проб: называние цифр, называние осмысленных изображений и называние цветов (переменные numbers, figures и colors соответственно). Время измерялось в секундах.
Исследователи предполагали, что среднее время выполнения проб может различаться у двух выделенных групп детей: отстающие справятся с заданием за большее время, чем хорошо успевающие.
В начале рассчитаем описательную статистку по пробе «называние цифр» в двух группах испытуемых с помощью функции describe.byиз пакета psych. В качестве аргумента зададим формулу в формате Зависимая переменная ~ Независимая переменная. В данном примере независимой переменной является номер группы, а зависимыми – времена выполнения трех проб. Соответственно, для оценки различий времени выполнения пробы на называние цифр в двух группах, формула выглядит так: numbers ~ group, для таблицы данных data_neuro:
library(foreign)
library(psych)
data_neuro <- read.spss("Neuro.sav", to.data.frame = T, reencode = "utf8")
describeBy(numbers ~ group, data = data_neuro)
Результат будет следующим:
Descriptive statistics by group group: poor students vars n mean sd median trimmed mad min max range skew kurtosis se X1 1 15 38.96 8.86 37.59 38.88 11.74 27.28 51.67 24.39 0.16 -1.61 2.29 ------------------------------------------------------------------------------------- group: good students vars n mean sd median trimmed mad min max range skew kurtosis se X1 1 15 28.96 6.07 28 28.54 5.04 20.62 42.8 22.18 0.68 -0.46 1.57
Также можно визуализировать результат сравнения средних в двух группах с помощью функции error.bars.byиз пакета psych, который при указании аргумента bars = TRUE, строит столбиковую диаграмму средних, а также отображает 95% доверительный интервал среднего для каждой из групп (так называемые столбики ошибок). При выполнении команды
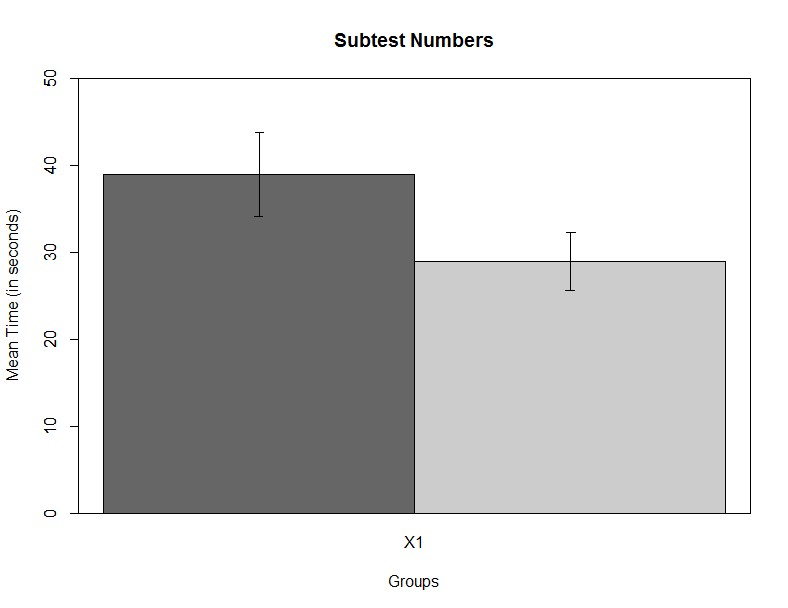
error.bars.by(numbers ~ group, data = data_neuro, bars = TRUE, ylim = c(0, 50), colors = c("grey40", "grey80"), main = "Subtest Numbers", xlab = "Groups", ylab = "Mean Time (in seconds)")
будет получен следующий график:
Рис. 6.3(9)r. Средние значения времени выполнения пробы на называние цифр.
Расчёты и график показал, что средние показатели времени выполнения проб различаются в двух группах, отстающие справлялись с заданием за большее время, чем дети из группы нормально успевающих: среднее время в секундах составило 38.96 и 28.96 соответственно. Для проверки статистической значимости гипотезы о равенстве средних в двух группах можно ответить с помощью с помощью Т-критерия Стьюдента для несвязанных выборок. Для этого можно воспользоваться уже знакомой нам функцией t.test, которая позволяет рассчитывать статистику Стьюдента и для несвязанных выборок, если задать в качестве первого аргумента формулу, аналогичную использованной выше и указать аргумент paired=FALSE. Рассмотрим результат расчёта t-критерия для переменной Numbers.
t.test(numbers ~ group, data = data_neuro, paired = FALSE) Welch Two Sample t-test data: data_neuro$numbers by data_neuro$group t = 3.6066, df = 24.785, p-value = 0.001363 alternative hypothesis: true difference in means between group отстающие and group хорошо успевающие is not equal to 0 95 percent confidence interval: 4.286958 15.713042 sample estimates: mean in group отстающие mean in group хорошо успевающие 38.96267 28.96267
По умолчанию в R Т-критерий рассчитывается с поправкой на неравенство дисперсий в двух сравниваемых выборках, так называемый критерий Уэлча (Welch). Как можно увидеть, статистика критерия в данном случае равна 3.6066, значимость полученного значения t-статистики, в данном случае чуть больше равна 0.001. Именно этой значимостью оцениваются различия среднего времени выполнения проб, характеризующих состояния энергетического блока мозга испытуемыми двух групп. Кратко результаты применения Т-критерия в данном случае, округляя результаты до трех знаков после запятой можно записать так: t(24.78)=3.607, p=0.001.
В результатах также приводится 95%-й доверительный интервал для разности: от 4.2869 до 15.7130 секунд — это напоминает нам, что различия в 10 секунд — это точечная оценка. Остается, однако, вопрос, что значат эти секунды с точки зрения различия развития функций.
На этот вопрос отвечают, оценивая величину эффекта. В данном случае разумная мера — отношение разности средних к некоему среднему стандартному отклонению выборок (квадратному корню из средней дисперсии). Выборочные дисперсии также приходится вычислять вручную, возводя в квадрат стандартные отклонения 8.85589 и 6.07397. Средняя дисперсия равна 57.66, корень из нее – 7.59, а 10/7.59=1.317. Выполнить этот расчёт в R можно с помощью функции cohen.dиз пакета effsize:
library(effsize) cohen.d(numbers ~ group, data = data_neuro) Cohen's d d estimate: 1.316931 (large) 95 percent confidence interval: lower upper 0.4918562 2.1420052
Обратите внимание, что помимо точечной оценки d Коэна, функция также рассчитывает 95% доверительный интервал.
Это и есть величина эффекта[5], которую в данном случае точнее называть мерой различия групп: средние по группам различаются на 1.317 стандартных отклонения. Некоторую визуализацию этой оценки дает рис. 6.3(10)r.
Рис. 6.3(10r). Так выглядели бы два нормальных распределения, средние которых отличаются на 1.125 стандартных отклонения. По аналогии можно представлять себе соотношение распределений характеристики недоразвития энергетического блока мозга (чем больше время на выполнение задания, тем хуже = слева успевающие, справа отстающие).
Упражнение 6.3(12). Повторите самостоятельно расчет Т-критерия с остальными двумя переменными из файла Neuro.sav.
Пример 6.3(13). Данные, представленные в файле recital1.sav (версия для SPSS, версия для Jamovi) моделируют результаты школьного изложения представителей двух параллельных учебных классов (кодируются переменной group). Переменная Time кодирует время, затраченное на работу, переменная Score – оценку содержания текста, переменная Mistakes – количество ошибок. В первой группе 10 человек, во второй 20. Между группами имеются весьма существенные различия в дисперсиях по двум из трех переменных. Наша задача – проиллюстрировать изложенное в предложении 6.2.2(1): как влияет на значимость неравенство дисперсий, когда сравниваемые выборки имеют разный объем.
Упражнение 6.3.(14).
Проделайте расчет Т-критерия для всех трех переменных. В SPSS и Jamovi их можно переместить в окно Проверяемые переменные (Dependent variables) одновременно, а в R надо три раза воспользоваться функцией t.test. При этом в R следует отдельно посчитать вариант без поправки на неравенство дисперсий, указав аргумент var.equal = TRUE.
Дисперсия переменной Time в меньшей группе существенно больше, что фиксируется критерием равенства дисперсий Ливиня[8]. Различия в оценках значимости между критериями, предполагающим и не предполагающим равенство дисперсий, достаточно серьезное.
Дисперсия переменной Time в меньшей группе существенно больше, что фиксируется критерием равенства дисперсий Ливиня. Различия в оценках значимости между критериями, предполагающим и не предполагающим равенство дисперсий, достаточно серьезное.
Дисперсия переменной Mistakes в меньшей группе, напротив, значительно меньше, чем в большей. Различие оценок значимости также велико, но направлено противоположно.
Дисперсии переменной Score примерно равны, и оценки значимости практически не различаются.
Полезно представить себя одновременно докладчиком курсовой работы, сообщающим эти результаты, и параллельно слушателем-оппонентом. Предположим, в докладе сообщалось только о значимости, полученной в предположении равенства дисперсий (первая строка таблицы). Что в каждом случае отметит критик? Попытайтесь сформулировать ответ самостоятельно, прежде чем читать наш ответ.
Ответ. Грамотный оппонент скажет о переменной Time: «Вы переоценили свой результат. На самом деле значимость вашего результата хуже, поэтому, собственно говоря, никакого результата нет. Вы заслуживаете оценки “неудовлетворительно”».
О переменной Mistakes оппонент скажет: «Вы недооценили свой результат. Если бы Вы, заметив неравенство дисперсий, применили более адекватный критерий оценки, то получили бы, что он еще лучше обоснован. Вы заслуживаете снижения оценки до “хорошо” за несовершенное знание статистики».
По поводу третьей переменной Score замечаний бы вообще не последовало.
Пример 6.3(15). В файле recital2.sav (версия для SPSS, версия для Jamovi) содержатся данные, аналогичные описанным в предыдущем задании, с теми же средними и дисперсиями, но при равных объемах выборок.
Упражнение 6.3(16). Убедитесь, что критерий Ливиня сообщает о еще более близкой к нулю значимости различий дисперсий (там, где они есть), поскольку несколько увеличились выборки. В то же время значимость различий средних оценивается критериями практически одинаково. Что изменилось бы в ситуации доклада результатов курсовой работы?
Ответ. Докладчику сделали бы только замечание, что он не сообщил о неравенстве дисперсий (действительно, в докладах такие вещи лучше говорить явно), но оценку бы не снизили.
Наши последние упражнения иллюстрируют рекомендацию всегда ориентироваться на вторую строку таблицы (равенство дисперсий не предполагается) и по возможности исследовать содержательно причины и следствия неравенства дисперсий, если они есть, поскольку это может оказаться неожиданным и интересным результатом исследования.
>> следующий параграф>>
[1] Hy L. X. et al. Measuring ego development. – Psychology Press, 2014.
[2] Согласно Дж.Левинжер, первая стадия развития характерна для младенчества и не встречается у детей школьного возраста и старше, поэтому методика не включает критериев ее оценки.
[3] Bandura A. Regulation of cognitive processes through perceived self-efficacy //Psychology of education. – 2000. – Т. 2. – С. 365-380.
[4] Denckla M. B., Rudel R. Rapid «automatized» naming of pictured objects, colors, letters and numbers by normal children //Cortex. – 1974. – Т. 10. – №. 2. – С. 186-202.
[5] Точнее, один из способов ее оценки, называющийся d Коэна
[6] Для появления этого пункта меню должен быть включён модуль scatr (про подключение и настройку модулей – см. Приложение 1.2.)
[7] Оно не рассчитывается функцией t.test, но его можно легко рассчитать, дав команду sd(data_rt$rt1 - data_rt$rt2)
[8] В R тест Ливиня можно рассчитать с помощью функции leveneTestиз пакета car:
library("foreign")
library("car")
data_recital <- read.spss("recital.sav", to.data.frame = T, reencode = "utf8")
leveneTest(Time ~ group, data = data_recital)